【数据结构和算法】时间空间复杂度分析
一、为什么要进行时间空间复杂度分析
1、数据结构和算法本身解决的是“快”和“省”的问题,即如何让代码运行得更快,如何让代码更省存储空间。所以,执行效率是算法一个非常重要的考量指标。只要讲到数据结构与算法,就一定离不开时间、空间复杂度分析。
2、事后统计法的局限性
- 测试结果非常依赖测试环境(软硬件的计算能力不同)
- 测试结果受数据规模的影响很大(数据规模和数据特点都会影响算法的执行效率)
3、需要一个不用具体的测试数据来测试,就可以粗略地估计算法的执行效率的方法
二、大O分析法[时间复杂度]
时间复杂度:全称就是渐进时间复杂度,表示算法的执行时间与数据规模之间的增长关系。
空间复杂度:全称就是渐进空间复杂度,表示算法的存储空间与数据规模之间的增长关系。
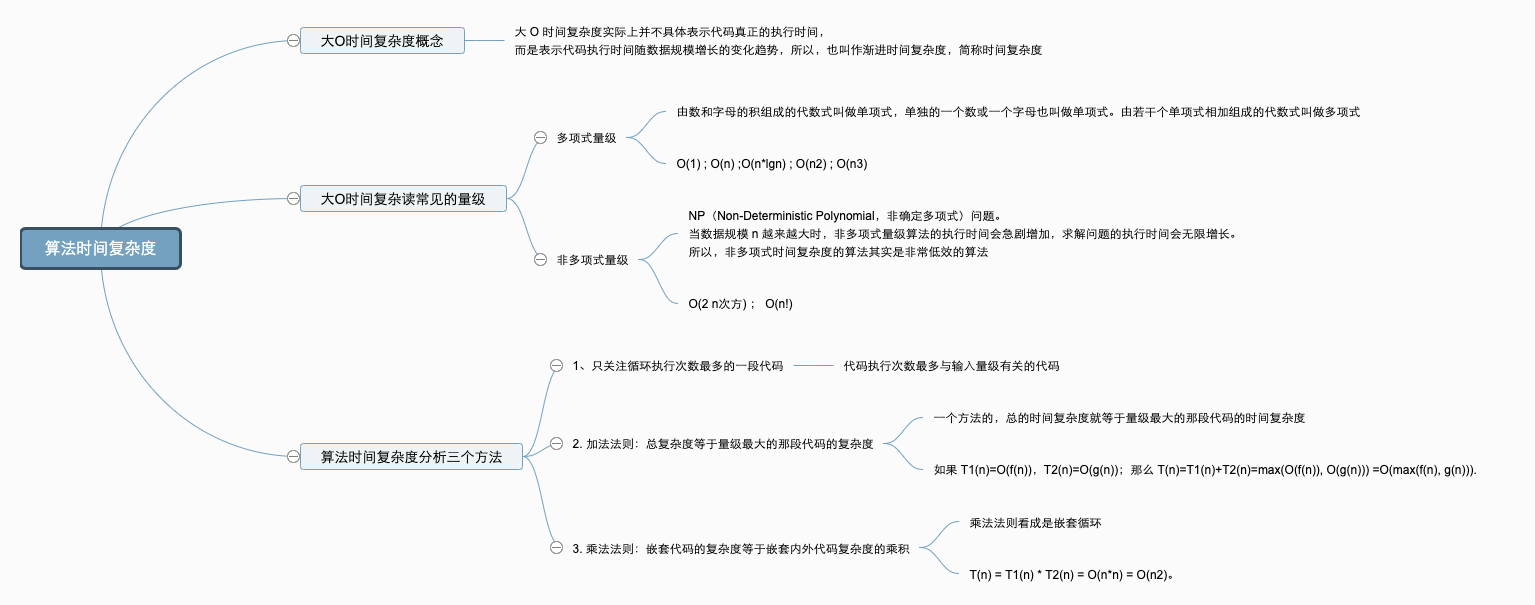
1、常见的时间复杂度

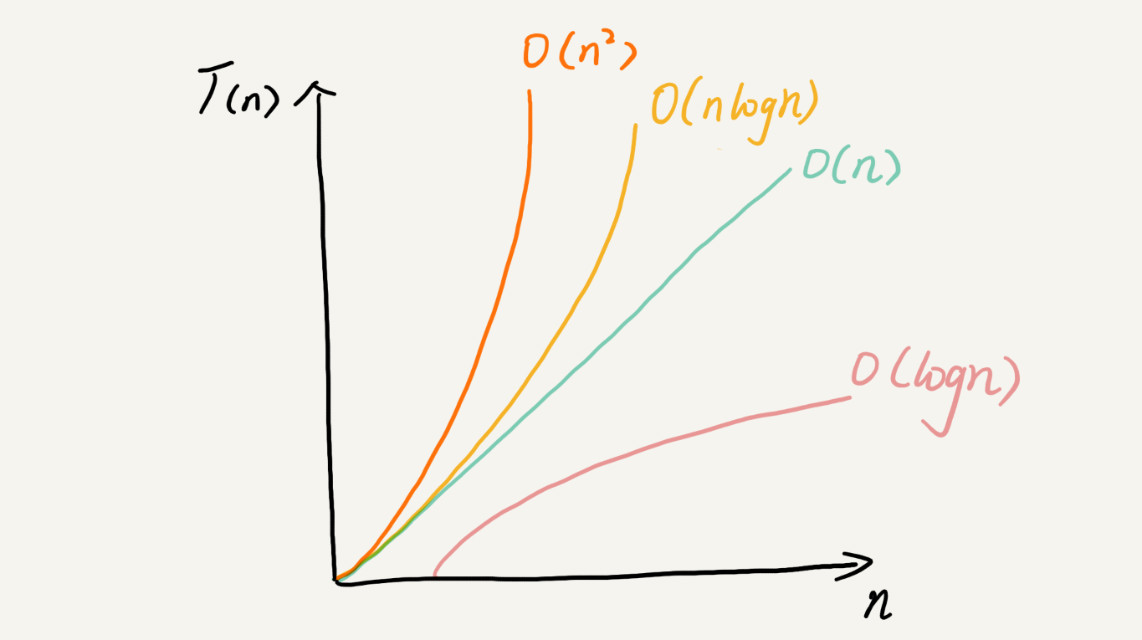
复杂度量级,我们可以粗略地分为两类,多项式量级和非多项式量级。其中,非多项式量级只有两个:O(2n) 和 O(n!)。
非多项式量级的算法问题叫作 NP(Non-Deterministic Polynomial,非确定多项式)问题。(至今无最优解的问题)
2、时间复杂度分析方式
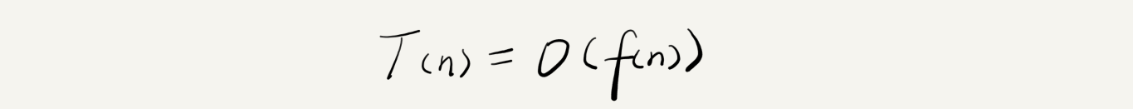
- T(n) :表示代码执行的时间
- n:表示数据规模的大小
- f(n) :表示每行代码执行的次数总和。因为这是一个公式,所以用 f(n) 来表示
- O:表示代码的执行时间 T(n) 与 f(n) 表达式成正比。

(1)只关注循环执行次数最多的一段代码
我们在分析一个算法、一段代码的时间复杂度的时候,也只关注循环执行次数最多的那一段代码就可以了
时间复杂度就是 O(n)

int cal(int n) { int sum = 0; int i = 1; for (; i <= n; ++i) { sum = sum + i; } return sum; }
(2)加法法则:总复杂度等于量级最大的那段代码的复杂度
总的时间复杂度就等于量级最大的那段代码的时间复杂度
T1(n)=O(f(n)),T2(n)=O(g(n));那么 T(n)=T1(n)+T2(n)=max(O(f(n)), O(g(n))) =O(max(f(n), g(n))).

int cal(int n) { int sum_1 = 0; int p = 1; for (; p < 100; ++p) { sum_1 = sum_1 + p; } int sum_2 = 0; int q = 1; for (; q < n; ++q) { sum_2 = sum_2 + q; } int sum_3 = 0; int i = 1; int j = 1; for (; i <= n; ++i) { j = 1; for (; j <= n; ++j) { sum_3 = sum_3 + i * j; } } return sum_1 + sum_2 + sum_3; }
(3)乘法法则:嵌套代码的复杂度等于嵌套内外代码复杂度的乘积
如果 T1(n)=O(f(n)),T2(n)=O(g(n));那么 T(n)=T1(n)*T2(n)=O(f(n))*O(g(n))=O(f(n)*g(n)).
也就是说,假设 T1(n) = O(n),T2(n) = O(n2),则 T1(n) * T2(n) = O(n3)。落实到具体的代码上,我们可以把乘法法则看成是嵌套循环

int cal(int n) { int ret = 0; int i = 1; for (; i < n; ++i) { ret = ret + f(i); } return ret; } int f(int n) { int sum = 0; int i = 1; for (; i < n; ++i) { sum = sum + i; } return sum; }
三、大O分析法[空间复杂度]
我们常见的空间复杂度就是 O(1)、O(n)、O(n2 ),像 O(logn)、O(nlogn) 这样的对数阶复杂度平时都用不到。而且,空间复杂度分析比时间复杂度分析要简单很多。

void print(int n) { int i = 0; int[] a = new int[n]; for (i; i < n; ++i) { a[i] = i * i; } for (i = n - 1; i >= 0; --i) { print out a[i] } }
空间复杂度为O(n)
四、最好,最坏,平均,均摊时间复杂度分析

// n表示数组array的长度 int find(int[] array, int n, int x) { int i = 0; int pos = -1; for (; i < n; ++i) { if (array[i] == x) { pos = i; break; } } return pos; }
最好时间复杂度:在最理想的情况下,执行这段代码的时间复杂度 O(1)
最坏情况时间复杂度:在最糟糕的情况下,执行这段代码的时间复杂度 O(n)
平均情况时间复杂度如何分析?
平均时间复杂度又该怎么分析呢?我还是借助刚才查找变量 x 的例子来给你解释。
要查找的变量 x 在数组中的位置,有 n+1 种情况:在数组的 0~n-1 位置中和不在数组中。我们把每种情况下,查找需要遍历的元素个数累加起来,然后再除以 n+1,就可以得到需要遍历的元素个数的平均值,即:
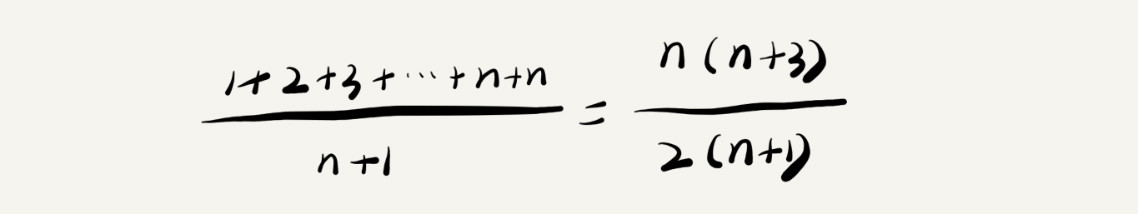
我们知道,时间复杂度的大 O 标记法中,可以省略掉系数、低阶、常量,所以,咱们把刚刚这个公式简化之后,得到的平均时间复杂度就是 O(n)。这个结论虽然是正确的,但是计算过程稍微有点儿问题。究竟是什么问题呢?我们刚讲的这 n+1 种情况,出现的概率并不是一样的。我带你具体分析一下。(这里要稍微用到一点儿概率论的知识,不过非常简单,你不用担心。)
我们知道,要查找的变量 x,要么在数组里,要么就不在数组里。这两种情况对应的概率统计起来很麻烦,为了方便你理解,我们假设在数组中与不在数组中的概率都为 1/2。另外,要查找的数据出现在 0~n-1 这 n 个位置的概率也是一样的,为 1/n。所以,根据概率乘法法则,要查找的数据出现在 0~n-1 中任意位置的概率就是 1/(2n)。因此,前面的推导过程中存在的最大问题就是,没有将各种情况发生的概率考虑进去。如果我们把每种情况发生的概率也考虑进去,那平均时间复杂度的计算过程就变成了这样:
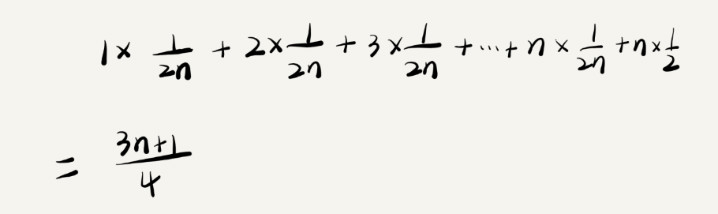
这个值就是概率论中的加权平均值,也叫作期望值,所以平均时间复杂度的全称应该叫加权平均时间复杂度或者期望时间复杂度。引入概率之后,前面那段代码的加权平均值为 (3n+1)/4。用大 O 表示法来表示,去掉系数和常量,这段代码的加权平均时间复杂度仍然是 O(n)。
五、均摊时间复杂度

// array表示一个长度为n的数组 // 代码中的array.length就等于n int[] array = new int[n]; int count = 0; void insert(int val) { if (count == array.length) { int sum = 0; for (int i = 0; i < array.length; ++i) { sum = sum + array[i]; } array[0] = sum; count = 1; } array[count] = val; ++count; }
最好情况时间复杂度为 O(1)
最坏情况时间复杂度为 O(n)
平均时间复杂度为O(1)
推导过程:
假设数组的长度是 n,根据数据插入的位置的不同,我们可以分为 n 种情况,每种情况的时间复杂度是 O(1)。除此之外,还有一种“额外”的情况,就是在数组没有空闲空间时插入一个数据,这个时候的时间复杂度是 O(n)。而且,这 n+1 种情况发生的概率一样,都是 1/(n+1)。所以,根据加权平均的计算方法,我们求得的平均时间复杂度就是:
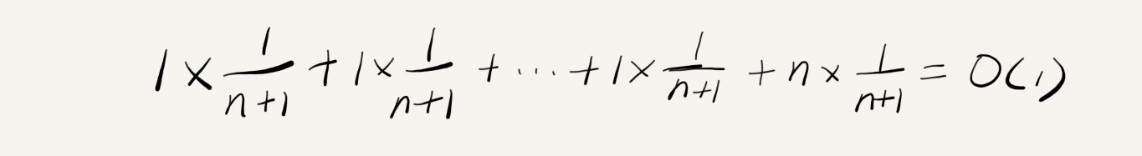
对一个数据结构进行一组连续操作中,大部分情况下时间复杂度都很低,只有个别情况下时间复杂度比较高,而且这些操作之间存在前后连贯的时序关系,这个时候,我们就可以将这一组操作放在一块儿分析,看是否能将较高时间复杂度那次操作的耗时,平摊到其他那些时间复杂度比较低的操作上。而且,在能够应用均摊时间复杂度分析的场合,一般均摊时间复杂度就等于最好情况时间复杂度。