【数据结构和算法】HashMap中的数据结构探究 和 currentHashMap并发原理
一、参考内容
https://www.cnblogs.com/wang-meng/p/9b6c35c4b2ef7e5b398db9211733292d.html
https://blog.csdn.net/weixin_43689776/article/details/99999126
二、基础知识部分
1、数据类型
2、数学运算
-
<< : 左移运算符,num << 1,相当于num乘以2 低位补0
举例:3 << 2
将数字3左移2位,将3转换为二进制数字0000 0000 0000 0000 0000 0000 0000 0011,然后把该数字高位(左侧)的两个零移出,其他的数字都朝左平移2位,最后在低位(右侧)的两个空位补零。则得到的最终结果是0000 0000 0000 0000 0000 0000 0000 1100,则转换为十进制是12。
数学意义:
在数字没有溢出的前提下,对于正数和负数,左移一位都相当于乘以2的1次方,左移n位就相当于乘以2的n次方。 -
>>: 右移运算符
举例:11 >> 2
则是将数字11右移2位,11 的二进制形式为:0000 0000 0000 0000 0000 0000 0000 1011,然后把低位的最后两个数字移出,因为该数字是正数,所以在高位补零。则得到的最终结果是0000 0000 0000 0000 0000 0000 0000 0010。转换为十进制是2。
数学意义:
右移一位相当于除2,右移n位相当于除以2的n次方。这里是取商哈,余数就不要了。 -
>>> : 无符号右移,忽略符号位,空位都以0补齐
按二进制形式把所有的数字向右移动对应位数,低位移出(舍弃),高位的空位补零。对于正数来说和带符号右移相同,对于负数来说不同。 其他结构和>>相似。 -
% : 模运算 取余
简单的求余运算 -
^ : 位异或 第一个操作数的的第n位于第二个操作数的第n位相反,那么结果的第n为也为1,否则为0
0^0=0, 1^0=1, 0^1=1, 1^1=0 -
& : 与运算 第一个操作数的的第n位于第二个操作数的第n位如果都是1,那么结果的第n为也为1,否则为0
0&0=0, 0&1=0, 1&0=0, 1&1=1 -
| : 或运算 第一个操作数的的第n位于第二个操作数的第n位 只要有一个是1,那么结果的第n为也为1,否则为0
0|0=0, 0|1=1, 1|0=1, 1|1=1 -
~ : 非运算 操作数的第n位为1,那么结果的第n位为0,反之,也就是取反运算(一元操作符:只操作一个数)
~1=0, ~0=1
3、hashMap中的hash算法
首先要明白一个概念,HashMap中定位到桶的位置 是根据Key的hash值与数组的长度取模来计算的。
具体的细节我就不说了,默认认为大家都懂这一点。
取模可以改为:hashCode & (length - 1) 与预算[ 1&1=1 , 1&0=0 , 0&1=1 ,0&0=0 ]
看下JDK8中的hash 算法:

static final int hash(Object key) { int h; return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16); }
首先是取key的hashCode算法,然后对16进行异或运算和右移运算。
在分析上面异或运算和右移运算问题之前,我们需要先看看另一个事情,什么呢?就是 HashMap 如何根据 hash 值找到数组种的对象,我们看看 get 方法的代码:

final Node<K,V> getNode(int hash, Object key) { Node<K,V>[] tab; Node<K,V> first, e; int n; K k; if ((tab = table) != null && (n = tab.length) > 0 && // 我们需要关注下面这一行 (first = tab[(n - 1) & hash]) != null) { if (first.hash == hash && // always check first node ((k = first.key) == key || (key != null && key.equals(k)))) return first; if ((e = first.next) != null) { if (first instanceof TreeNode) return ((TreeNode<K,V>)first).getTreeNode(hash, key); do { if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k)))) return e; } while ((e = e.next) != null); } } return null; }
我们看看代码中注释下方的一行代码:first = tab[(n - 1) & hash])。
使用数组长度减一 与运算 hash 值。这行代码就是为什么要让前面的 hash 方法移位并异或。
** 我们分析一下:**
首先,假设有一种情况,
对象 A 的 hashCode 为 0100 0010 0011 1000 1000 0011 1100 0000,
对象 B 的 hashCode 为 0011 1011 1001 1100 0101 0000 1010 0000。
如果数组长度是16,也就是 15 与运算这两个数(前面说的hashCode & (length - 1)), 你会发现结果都是0。这样的散列结果太让人失望了。很明显不是一个好的散列算法。
但是如果我们将 hashCode 值右移 16 位,也就是取 int 类型的一半,刚好将该二进制数对半切开。并且使用位异或运算(如果两个数对应的位置相反,则结果为1,反之为0),这样的话,就能避免我们上面的情况的发生。简而言之就是尽量打乱hashCode的低16位,因为真正参与运算的还是低16位。
不知道这种解释是否是简单明了,经过自己的思考和分析后 也明白了 这段代码设计的初衷,也会感叹设计者的精妙。
三、如何解决Hash冲突的方法
1、链表法 (常用)
2、开放寻址法 (常用)
3、再hash
4、建立公共溢出区
1、链表法
在哈希表中,每一个桶(bucket)或者槽(slot)都会对应一条链表,所有哈希值相同的元素放到相同槽位对应的链表中。
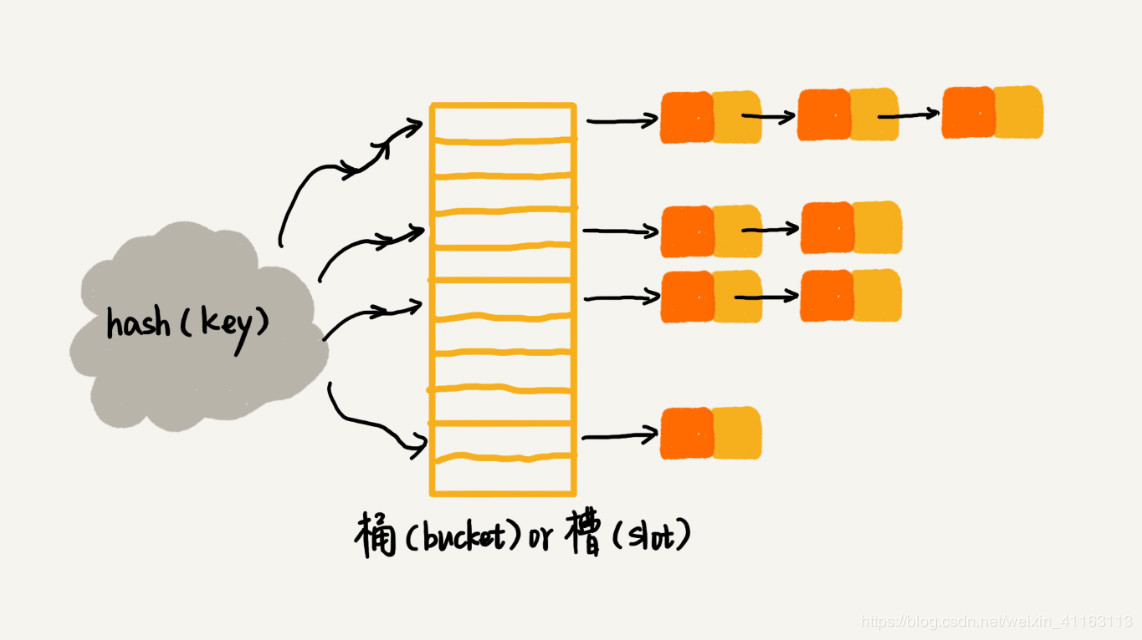
在插入的时候,我们可以通过散列函数计算出对应的散列槽位,将元素插入到对应的链表即可,时间复杂度为O(1);在查找或删除元素时,我们同样通过散列函数计算出对应的散列槽位,然后再通过遍历链表进行查找或删除,时间复杂度为O(k),k为链表长度。
2、开放寻址法
核心思想:如果出现散列冲突,我们就重新探测一个空闲位置,再将元素插入。
一种比较简单的探测方法:线性探测法(Linear Probing)
但我们往散列表中插入元素时,如果某个数据经过散列函数散列之后,存储位置已经被占用了,那么我们就从当前位置开始,依次往后遍历,直到找到空余的位置插入为止(插入第一个空余的位置,方便查找),举例如图:
黄色的色块表示空余色块,橙色的色块表示已经存储了数据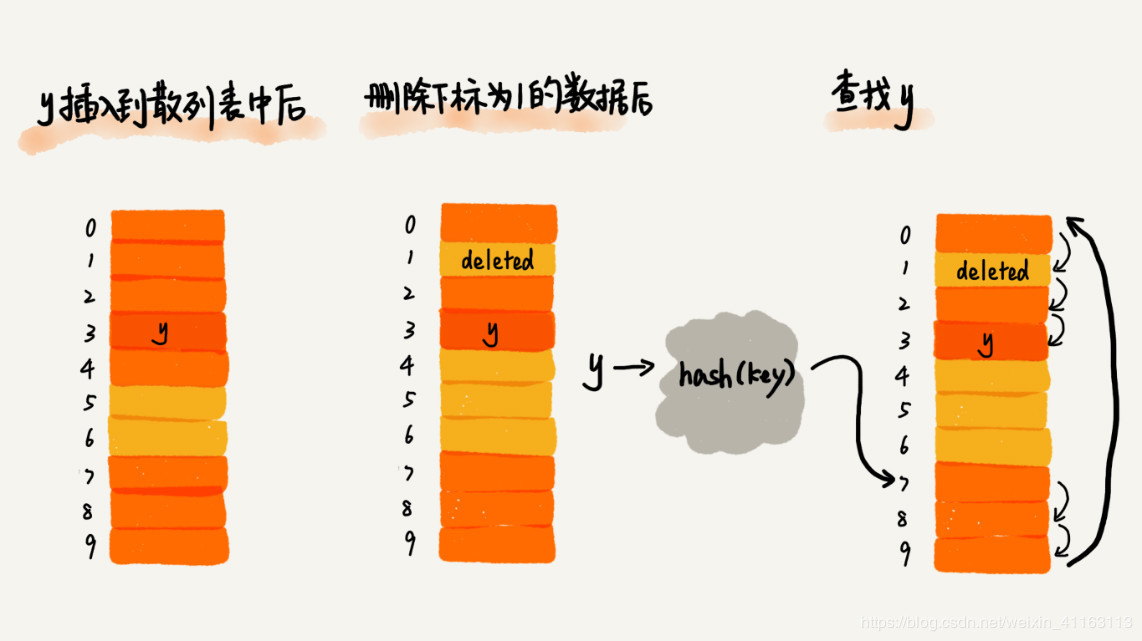
在查找元素时,先将要查找元素键值通过散列函数变成散列值,然后与下标为散列值的元素比较,若相等,则说明这是我们要找的元素;若不相等,则顺序往后遍历查找,如果遍历到数组中的空余位置还是没有找到,说明要查找的元素不在散列表中。
删除元素时,删除操作不能简单地把元素设置为空,而是要特殊标记为deleted,因为如果简单设置为空,在查找元素的过程中遇到这个被删除元素的位置就会停下,而不是继续往后遍历,会使查找算法失效;但是如果特色标记为deleted,当线性探测查找时,遇到标记为deleted的位置就会往下探测。
线性探测法的缺点:当插入的数据越来越多时,散列冲突发生的可能性会越来越大,空余位置会越来越少,线性探测的时间会越来越长,最坏时间复杂度为O(n)。
3、再hash
这种方法是同时构造多个不同的哈希函数:
Hi=RH1(key) i=1,2,…,k
当哈希地址Hi=RH1(key)发生冲突时,再计算Hi=RH2(key)……,直到冲突不再产生。这种方法不易产生聚集,但增加了计算时间。
===具体应用===
布隆过滤器算法应用该思想,对同一个值进行多次hash,在数组上多个位置占位。如果一个数据多次hash在多个位置上都存在,表示有可能在黑名单中(存在hash冲突的场景)。
如果有其中几个未命中,表示一定不在黑名单中。
4、建立公共溢出区
这种方法的基本思想是:将哈希表分为基本表和溢出表两部分,凡是和基本表发生冲突的元素,一律填入溢出表
四、HashMap是如何减少hash冲突,保证数据散列的
事实上,想让hash冲突完全不发生,是不太可能的,我们能做的只是尽可能的降低hash冲突发生的概率:下面介绍在HashMap中是如何应对hash冲突的?
当我们向hashmap中put元素(key, value)时,最终会执行putVal()方法,而在putVal()方法中,又执行了hash(key)这个操作,并将执行结果作为参数传递给了putVal方法。那么我们先来看hash(key)方法干了什么。

public V put(K key, V value) { return putVal(hash(key), key, value, false, true); } static final int hash(Object key) { int h; // 判断key是否为null, 如果为null,则直接返回0; // 如果不为null,则返回(h = key.hashCode()) ^ (h >>> 16)的执行结果 return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16); }
(h = key.hashCode()) ^ (h >>> 16) 执行了三步操作 :我们一步一步来分析:
- 第1步:h = key.hashCode()
这一步会根据key值计算出一个int类型的h值也就是hashcode值,例如
"helloWorld".hashCode() --> -1554135584 "123456".hashCode() --> 1450575459 "我爱java".hashCode() --> -1588929438
至于hashCode()是如何根据key计算出hashcode值的,要分几种情况进行分析:
1. 如果我们使用的自己创建的对象,在我们没有重写hashCode()方法的情况下,会调用Object类的hashCode()方法,而此时返回就是对象的内存地址值,所以如果对象不同,那么通过hashcode()计算出的hashcode就是不同的。
2. 如果是使用java中定义的引用类型例如String,Integer等作为key,这些类一般都会重写hashCode()方法,有兴趣可以翻看一下对应的源码。简单来说,Integer类的hashCode()返回的就是Integer值,而String类型的hashCode()方法稍稍复杂一点,这里不做展开。总的来说,hashCode()方法的作用就是要根据不同的key得到不同的hashCode值。
- 第2步:h >>> 16
为什么要右移16位,当然是位了第三步的操作。
- 第3步:h ^ (h >>> 16)
将hashcode值的高低16位进行异或操作(同0得0、同1得0、不同得1)得到hash值,举例说明:
假设h值为:1290846991 它的二进制数为:01001100 11110000 11000011 00001111 右移十六位之后:00000000 00000000 01001100 11110000 进行异或操作后:01001100 11110000 10001100 11110000 最终得到的hash值:1290833136
那么问题来了: 明明通过第一步得到的hashcode值就可以作为hash返回,为什么还要要进行第二步和第三步的操作呢?答案是为了减少hash冲突!
元素在数组中存放的位置是由下面这行代码决定的:
// 将(数组的长度-1)和hash值进行按位与操作: i = (n - 1) & hash // i为数组对应位置的索引 n为当前数组的大小
我们将上面这步操作作为第4步操作,来对比一下执行1、2、3、4四个步骤和只执行第1、4两个步骤所产生的不同效果。
我们向hashmap中put两个元素node1(key1, value1)、node2(key2, value2),hashmap的数组长度n=16。
执行1、2、3、4 四个步骤:
1. h = key.hashCode() 假设计算的结果为:h = 3654061296 对应的二进制数为: 01101100 11100110 10001100 11110000 2. h >>> 16 h无符号右移16位得到: 00000000 00000000 01101100 11100110 3. hash = h ^ (h >>> 16) 异或操作后得到hash: 01101100 11110000 11100000 00000110 4. i = (n-1) & hash n-1=15 对应二进制数 : 00000000 00000000 00000000 00001111 hash : 01101100 11110000 11100000 00000110 hash & 15 : 00000000 00000000 00000000 00000110 转化为10进制 : &ensp 5
最终得到i的值为5,也就是说node1存放在数组索引为5的位置。
同理我们对(key2, value2) 进行上述同样的操作过程:
1. h = key.hashCode() 假设计算的结果为:h = 3652881648 对应的二进制数为: 01101100 11011101 10001100 11110000 2. h >>> 16 h无符号右移16位得到: 00000000 00000000 01101100 11011101 3. hash = h ^ (h >>> 16) 异或操作后得到hash: 01101100 11110000 11100000 00101101 4. i = (n-1) & hash n-1=15 对应二进制数 : 00000000 00000000 00000000 00001111 hash : 01101100 11110000 11100000 00101101 hash & 15 : 00000000 00000000 00000000 00001101 转化为10进制 : &ensp 13
最终得到i的值为13,也就是说node2存放在数组索引为13的位置
node1和node2存储的位置如下图所示:

执行1、4两个步骤:
1. h = key.hashCode() 计算的结果同样为:h = 3654061296 对应的二进制数为: 01101100 11100110 10001100 11110000 4. i = (n-1) & hash n-1=15 对应二进制数 : 00000000 00000000 00000000 00001111 hash(h) : 01101100 11100110 10001100 11110000 hash & 15 : 00000000 00000000 00000000 00000000 转化为10进制 : 0
最终得到i的值为0,也就是说node1存放在数组索引为0的位置
同理我们对(key2, value2) 进行上述同样的操作过程:
1. h = key.hashCode() 计算的结果同样为:h = 3652881648 对应的二进制数为: 01101100 11011101 10001100 11110000 4. i = (n-1) & hash n-1=15 对应二进制数 : 00000000 00000000 00000000 00001111 hash(h) : 01101100 11110000 11100000 11110000 hash & 15 : 00000000 00000000 00000000 00000000 转化为10进制 : 0
最终得到i的值为0,也就是说node2同样存放在数组索引为0的位置
node1和node2存储的位置如下图所示:

相信大家已经看出区别了:
当数组长度n较小时,n-1的二进制数高16位全部位0,这个时候如果直接和h值进行&(按位与)操作,那么只能利用到h值的低16位数据,这个时候会大大增加hash冲突发生的可能性,因为不同的h值转化为2进制后低16位是有可能相同的,如上面所举例子中:key1.hashCode() 和key2.hashCode() 得到的h值不同,一个h1 = 3654061296 ,另一个h2 = 3652881648,但是不幸的是这h1、h2两个数转化为2进制后低16位是完全相同的,所以h1 & (n-1)和 h2 & (n-1) 会计算出相同的结果,这也导致了node1和node2 存储在了数组索引相同的位置,发生了hash冲突。
当我们使用进行 h ^ (h >>> 16) 操作时,会将h的高16位数据和低16位数据进行异或操作,最终得出的hash值的高16位保留了h值的高16位数据,而hash值的低16数据则是h值的高低16位数据共同作用的结果。所以即使h1和h2的低16位相同,最终计算出的hash值低16位也大概率是不同的,降低了hash冲突发生的概率。
ps:这里面还有一个值的注意的点: 为什么是(n-1)?
我们知道n是hashmap中数组的长度,那么为要进行n-1的操作?答案同样是为了降低hash冲突发生的概率!
要理解这一点,我们首先要知道HashMap规定了数组的长度n必须为2的整数次幂,至于为什么是2的整数次幂,会在HashMap的扩容方法resize()里详细讲。
既然n为2的整数次幂,那么n一定是一个偶数。那么我们来比较i = hash & n和 i = hash & (n-1)有什么异同。
n为偶数,那么n转化为2进制后最低位一定为0,与hash进行按位与操作后最低位仍一定为0,这就导致i值只能为偶数,这样就浪费了数组中索引为奇数的空间,同时也增加了hash冲突发生的概率。
所以我们要执行n-1,得到一个奇数,这样n-1转化为二进制后低位一定为1,与hash进行按位与操作后最低位即可能位0也可能位1,这就是使得i值即可能为偶数,也可能为奇数,充分利用了数组的空间,降低hash冲突发生的概率。
五、HashMap做扩容的时候,如何处理冲突链表的重新定位
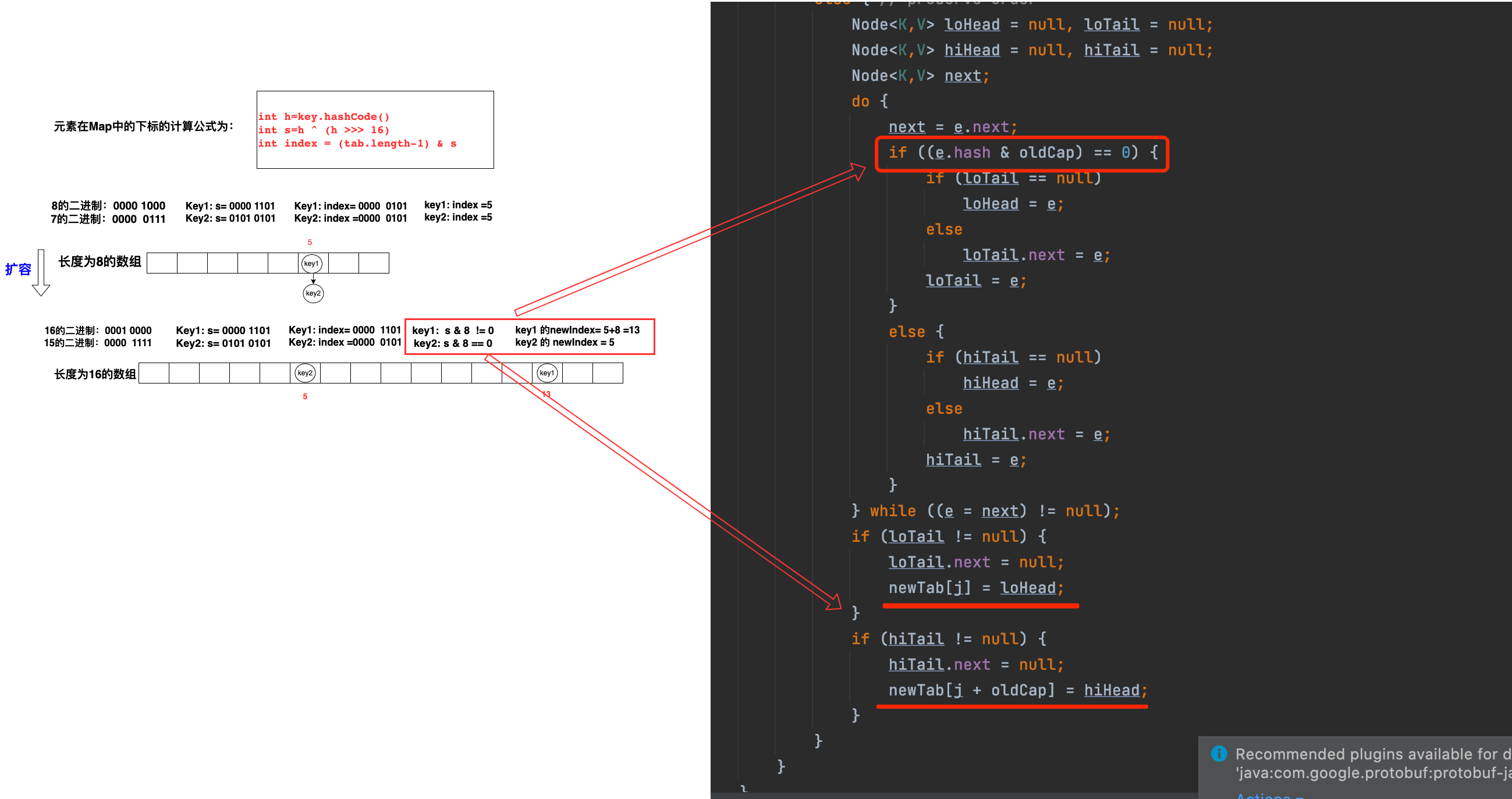
链表转红黑树的前置条件:(1)存储数据数组的长度需大于等于64 (2)链表冲突后,链表元素的个数需大于等于8个
hashmap的扩展因子:0.75
hashMap的扩展条件:元素个数>= 数组长度*0.75
五、currentHashMap并发原理
jdk 1.8 的ConcurrentHashMap取消了segment分段锁,
而采用CAS和synchronized来保证并发安全。数据结构跟HashMap1.8的结构一样,数组+链表/红黑二叉树。
synchronized只锁定当前链表或红黑二叉树的首节点,这样只要hash不冲突,就不会产生并发,效率又提升N倍。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号