【数据结构和算法】算法导论=>数组相关的算法

一、排序类

参考：https://www.runoob.com/w3cnote/ten-sorting-algorithm.html

1、插入排序 O(n^2)

public class Sort {

    public static void main(String[] args) {
        int[] a={9,7,5,6,4,3,1,2,8};
        int[] sortArray=insertSort(a);
        System.out.println(Arrays.toString(sortArray));


    }


    /**
     * 插入排序
     *
     * 学习一个算法的过程
     * （1）理解思路，能证明其正确性
     * （2）分析算法的时间复杂度
     *
     *
     *=>算法的整体设计策略：增量策略
     *=>算法实现的思路：
     * （1）以数组中的第一个元素为初始子数组（有序）
     * （2）从数组的第二个元素其，遍历完数组剩余的元素，依次构建有序的子数组
     *
     *
     * int[] a={9,7,5,6,4,3,1,2,8};
     *=>循环不变式证明（目标：帮助我们理解算法的正确性）
     * （1）初始化：未进行迭代前，循环不变式为真；   未开始迭代前子数组为{9},该数组有序。
     * （2）保持：某次迭代前为真，下次迭代前依然为真；  比如要进行第二次迭代前子数组为{7,9},则第三次迭代前子数组为{5,7,9},该子数组依然有序
     * （3）终止：循环终止，循环不变式为我们提供1个有用的性质，该性质有助于我们证明算法的正确性；  当循环终止，子数组的元素个数与原数组个数一致，且有序
     *
     *
     *=>算法的时间复杂度（sort.length=m ,待排序数组元素为n）
     * O(n ^2)
     * @param sort
     * @return
     */
    public  static int[] insertSort(int[] sort){
        for(int j=1;j<sort.length;j++){                 // 执行n次
            int value=sort[j];                          //执行 n-1次
            int i=j-1;                                  //执行 n-1 次
            while (i>=0&&sort[i]>value){                // 1+2+3+...+(n-1)
                sort[i+1]=sort[i];                      // 1+2+3+...+(n-2)
                i--;                                    // 1+2+3+...+(n-2)
            }
            sort[i+1]=value;                              //执行 n-1次
        }
        return sort;
    }

}

2、归并排序O(n *log n)

public class Sort {

    public static void main(String[] args) {
        int[] a = {9, 7, 5, 6, 4, 3, 1, 2, 8,0,8};
        int[] sortArray = mergeSort(a);
        System.out.println(Arrays.toString(sortArray));


    }




    /**
     * 归并排序（二分排序法）
     *
     * 学习一个算法的过程
     * （1）理解思路，能证明其正确性
     * （2）分析算法的时间复杂度
     *
     * =>算法的整体设计策略：分治策略
     *
     *
     * =>分治算法的思路
     * （1）分解：分解原问题为若干个子问题，这些子问题是原文的规模较小的实例
     * （2）解决：解决这些子问题，递归地求解各个子问题。然而，若子问题规模足够小，则直接求解
     * （3）合并：合并这些子问题的解，成为原问题的解
     *
     * =>算法的时间复杂度
     * （1）O(n log n)
     *
     * @param array
     * @return
     */
    public static  int[] mergeSort(int[] array) {
        int length = array.length;
        int[] newArray = mergeSort(array, 0, length - 1);
        return newArray;
    }


    public static int[] mergeSort(int[] array, int startIndex, int endIndex) {
        //如果起始下标和结束下标相同,则代表问题已经拆解到最小，1个元素就是有序数组，递归触底，不用再拆解了，返回新数组
        if (startIndex == endIndex) {
            return new int[]{array[startIndex]};
        }
        //分解问题
        int mid = mid(startIndex, endIndex);
        //递归解决子问题
        int[] leftArray = mergeSort(array, startIndex, mid);
        int[] rightArray = mergeSort(array, mid + 1, endIndex);
        //合并解决两个子问题的结果
        return merge(leftArray, rightArray);
    }

    /**
     * 求中位数
     *
     * @param startIndex
     * @param endIndex
     * @return
     */
    public static int mid(int startIndex, int endIndex) {
        return (startIndex + endIndex) / 2;
    }

    /**
     * 求合并结果
     *
     * @param left
     * @param right
     * @return
     */
    public static int[] merge(int[] left, int[] right) {
        int leftLength = left.length;
        int rightLength = right.length;

        int[] newArray = new int[leftLength + rightLength];
        int leftIndex = 0;
        int rightIndex = 0;
        int newArrayIndex = 0;

        while (true) {
            //遍历左侧数组（让左侧数组的元素依次和右侧数组的参照元素进行对比）
            while (leftIndex < leftLength && rightIndex<rightLength) {
                if (left[leftIndex] <= right[rightIndex]) {
                    newArray[newArrayIndex++] = left[leftIndex];
                    leftIndex++;
                } else {
                    //左侧的元素有一个数，大于右侧的参照数据，跳出循环
                    break;
                }
            }
            //遍历右侧数组（让右侧数组的元素依次和左侧的参照数据对比）
            while (rightIndex < rightLength && leftIndex<leftLength) {
                if (right[rightIndex] < left[leftIndex]) {
                    newArray[newArrayIndex++] = right[rightIndex];
                    rightIndex++;
                } else {
                    //右侧的元素有一个数，大于左侧的参照数据，跳出循环
                    break;
                }
            }

            //两个数组都未遍历完,则需要进行下一次参照对比。
            //如果有一个数组对比完，说明有一个数组的元素已经全部放入新序列，剩下的数组只需要补齐即可
            if (leftIndex < leftLength && rightIndex < rightLength) {
                continue;
            }
            //补全左侧数组
            if (leftIndex < leftLength) {
                for (; leftIndex < leftLength; leftIndex++) {
                    newArray[newArrayIndex++] = left[leftIndex];
                }
            }

            //补全右侧数组
            if (rightIndex < rightLength) {
                for (; rightIndex < rightLength; rightIndex++) {
                    newArray[newArrayIndex++] = right[rightIndex];
                }
            }
            break;
        }
        return newArray;
    }
}

3、快速排序 [最坏的情况O(n^2) 平均情况O（n*logn）]

public class QuickSort {

    public static void main(String[] args) {
        int[] array = {4, 9, 0, 1, 4, 6, 10, 8};
        quickSort(array, 0, array.length - 1);
        System.out.println(Arrays.toString(array));
    }


    public static void quickSort(int[] array, int beginIndex, int endIndex) {
        //求出调整的位置
        int mid = sort(array, beginIndex, endIndex);
        //当开始元素=结束元素，则表示为1个元素的子数组，无需排序
        if (beginIndex < mid) {
            //排序左侧子数组
            quickSort(array, beginIndex, mid - 1);
        }
        //当开始元素=结束元素，则表示为1个元素的子数组，无需排序
        if (mid < endIndex) {
            //排序右侧子数组
            quickSort(array, mid + 1, endIndex);
        }

    }

    public static int sort(int[] array, int beginIndex, int endIndex) {
        int data = array[beginIndex];
        int leftIndex = beginIndex;
        int rightIndex = endIndex;

        //左侧哨兵下标不等于右侧哨兵下标
        while (leftIndex != rightIndex) {
            //右侧哨兵开始向左探测
            for (; array[rightIndex] > data && (leftIndex < rightIndex); rightIndex--) {
                System.out.println("右侧哨兵开始向左探测");
            }
            //左侧哨兵开始向右探测
            for (; array[leftIndex] <= data && (leftIndex < rightIndex); leftIndex++) {
                System.out.println("左侧哨兵开始向右探测");
            }

            //左右哨兵都遇到需要被交换的元素，进行元素交换
            if (leftIndex < rightIndex) {
                int tmp = array[leftIndex];
                array[leftIndex] = array[rightIndex];
                array[rightIndex] = tmp;
            }

            //哨兵相遇，表示该点可以和基准元素进行位置交换
            if (leftIndex == rightIndex) {
                array[beginIndex] = array[leftIndex];
                array[leftIndex] = data;
            }
        }
        return leftIndex;
    }
}

5、冒泡排序

public class BubbleSort {

    public static void main(String[] args) {
        int[] target={100,9,87,5,8,5,9,13};
        int[] result=bubbleSort(target);
        System.out.println(Arrays.toString(result));
    }


    public static int[] bubbleSort(int[] array){
        if(array==null || array.length==1){
            return array;
        }
        for(int i=0;i<array.length;i++){
            boolean isHappenedExchange=false;
            int tmp=0;
            for(int j=0;j<array.length-i-1;j++){
                if(array[j]>array[j+1]){
                    tmp=array[j+1];
                    array[j+1]=array[j];
                    array[j]=tmp;
                    isHappenedExchange=true;
                }
            }
            if(!isHappenedExchange){
                break;
            }
        }
        return array;
    }
}

6、最小堆基于循环实现 [O(logn)]

package com.sxf.study.inter.heap;

import java.util.Arrays;

/**
 */
public class BinaryHeap {

    private static int count = 0;

    private static int[] array = new int[10];

    /**
     * 最小二叉堆的操作：
     * 【1】插入元素：将元素放到数组最后1位，向上调整，和父亲节点比较
     * 【2】取出元素：从第一个位置取出一个元素，将最后一个元素放到第一个位置，和左右孩子中最小的比较，向下调整。
     *
     * 将一个数组调整为二叉堆
     * 从最后的非叶子节点，依次向上调整
     *
     * @param args
     */
    public static void main(String[] args) {
        int[] a = {6, 9, 0, 4, 3, 1, 10, 3};
        siftBinaryHeap(a);
        //输出 [0, 3, 1, 4, 3, 6, 10, 9]
    }


    public static void siftBinaryHeap(int[] array) {
        int lastParentIndex = (array.length - 2) / 2;
        for (int i = lastParentIndex; i >= 0; i--) {
            siftDown(array, array.length, array[i], i);
        }
        System.out.println(Arrays.toString(array));
    }

    /**
     * 向二叉堆中添加1个元素
     *
     * @param data
     */
    public static void add(int data) {
        //元素个数+1
        count++;
        //从最后1个位置向上调整元素
        siftUp(array, data, count - 1);
    }

    /**
     * 从二叉堆中取走1个元素
     *
     * @return
     */
    public static int poll() {
        //取出第一个元素作为结果
        int result = array[0];
        //从最后一个位置拿出待调整的元素
        int siftData = array[count - 1];
        //将最后一个位置设置为null
        array[count - 1] = 0;
        //堆中元素个数-1
        count--;
        //向下调整堆
        siftDown(array, count, siftData, 0);
        return result;
    }


    /**
     * 已知父节点，求子节点的下标的公式
     * leftIndex=2*parentIndex+1
     * rightInde=2*parentIndex+2
     * 已知子节点，求父节点下标的公式
     * parentIndex=(childIndex-1)/2
     *
     *
     * count代表数组中的元素总数（包含被即将添加进来的）
     *
     * @param array      数组
     * @param data       当前要插入的数据
     * @param childIndex 最后一个孩子节点的位置（count-1）
     */
    private static void siftUp(int[] array, int data, int childIndex) {
        //调整至最定点的位置，及下标为0的位置。
        while (childIndex > 0) {
            int parentIndex = parentIndex(childIndex);
            int parentData = array[parentIndex];
            if (parentData > data) {
                //需要换位置
                array[childIndex] = parentData;
                childIndex = parentIndex;
            } else {
                break;
            }
        }
        array[childIndex] = data;
    }

    /**
     * @param array       数组
     * @param count       数组中元素的个数（不包含即将被取走的最小元素）
     * @param data
     * @param parentIndex
     */
    private static void siftDown(int[] array, int count, int data, int parentIndex) {
        //调整至最后一个元素的位置,第一个没有孩子的下标。
        int firstNoHaveChildIndex = (count - 1) / 2 + 1;
        while (parentIndex < firstNoHaveChildIndex) {
            int childIndex = leftChildIndex(parentIndex);
            int childData = array[childIndex];
            int rightIndex = childIndex + 1;
            if (rightIndex <= (count - 1)) {
                //存在右侧节点，如果右侧节点小于左侧节点，则比较的的元素为右侧节点
                if (childData > array[rightIndex]) {
                    childIndex = rightIndex;
                    childData = array[rightIndex];
                }
            }
            if (data > childData) {
                //如果待调整的元素依然大于两个孩子中最小的那个,则进行位置互换
                array[parentIndex] = childData;
                parentIndex = childIndex;
            } else {
                //待调整节点大于两个子节点，中断调整
                break;
            }
        }
        array[parentIndex] = data;
    }


    private static int parentIndex(int childIndex) {
        return (childIndex - 1) / 2;
    }

    private static int leftChildIndex(int parentIndex) {
        return parentIndex * 2 + 1;
    }

}

7、最小堆基于递归实现

public class MinHeap {
    /**
     * 堆容量
     */
    private int capacity;
    /**
     * 当前堆中元素
     */
    private int count;
    /**
     * 存放堆元素的容器 (定义为public 便于测试)
     */
    public  int[] heapArray;


    public MinHeap(int capacity) {
        this.capacity = capacity;
        this.heapArray = new int[capacity];
        this.count = 0;
    }

    /**
     * 向最小堆添加1个元素
     *
     * @param data
     * @return
     */
    public void addData(int data) {
        //step1:判断容量
        if (this.count == this.capacity) {
            //堆中存放元素已满,进行扩容
            resizeHeap();
        }
        //step2:加入数组,变更相应属性。加入到数组末尾
        this.count++;
        this.heapArray[this.count - 1] = data;
        //step3:对加入堆中的元素,进行向上调整
        upSift(count-1);
    }

    /**
     * 从最小堆取出1个元素
     *
     * @return
     */
    public int pullData() {
        //step1:判断堆中是否有元素,没有元素返回-1;
        if (this.count == 0) {
            //返回-1
            return -1;
        }
        //step2:取出第一个元素作为结果,并将最后一个元素,移动至第一个位置
        int result = this.heapArray[0];
        if (this.count > 1) {
            this.heapArray[0] = this.heapArray[this.count - 1];
            this.heapArray[this.count - 1] = -1;
            this.count--;
            //step3:向下调整
            downSift(0);
            return result;
        }
        this.count--;
        return result;
    }

    /**
     * 扩容堆
     */
    public void resizeHeap() {
        int newCapacity = this.capacity * 2;
        int[] newHeapArray = new int[newCapacity];
        for (int i = 0; i < capacity; i++) {
            newHeapArray[i] = this.heapArray[i];
        }
        this.capacity = newCapacity;
        this.heapArray = newHeapArray;
    }

    /**
     * 向下调整
     *
     * @param index
     */
    private void downSift(int index) {
        int leftChildData = leftChildData(index);
        int rightChildData = rightChildData(index);
        //step1:临界条件判断,两个孩子节点均为空，则不用继续调整
        if (leftChildData == -1 && rightChildData == -1) {
            //左右孩子节点都为空,则不用再继续调整了
            return;
        }
        //step2:找到左右孩子的最小节点
        int minIndex = -1;
        int minData = -1;
        if (leftChildData != -1) {
            minIndex = 2 * index + 1;
            minData = leftChildData;
            if (rightChildData != -1 && rightChildData < leftChildData) {
                minIndex = 2 * index + 2;
                minData = rightChildData;
            }
        }

        //step3:和最小孩子进行比较,看是否需要进行交换，如需交换,交换完则继续向下调整
        if (this.heapArray[index] > minData) {
            //数据交换
            int tmp = this.heapArray[index];
            this.heapArray[index] = minData;
            this.heapArray[minIndex] = tmp;
            //继续向下调整
            downSift(minIndex);
        }
    }


    /**
     * 向上调整
     *
     * @param index
     */
    private void upSift(int index) {
        if (index <= 0) {
            //说明已经调整到根节点了,无需再继续进行调整
            return;
        }
        boolean happenedSift = false;
        int parentIndex = (index - 1) / 2;
        int parentData = this.heapArray[parentIndex];
        int tmp = -1;
        if (parentData > this.heapArray[index]) {
            //如果父亲节点大于当前孩子节点,则进行位置调换
            tmp = this.heapArray[index];
            this.heapArray[index] = parentData;
            this.heapArray[parentIndex] = tmp;
            happenedSift = true;
        }
        if (happenedSift) {
            //如果本次比较发生过调整,则继续向上调整
            upSift(parentIndex);
        }
    }


    /**
     * 获取某一个节点的父亲节点
     *
     * @param childIndex
     * @return
     */
    private int parentData(int childIndex) {
        if (childIndex <= 0) {
            return -1;
        }
        int parentIndex = (childIndex - 1) / 2;
        return this.heapArray[parentIndex];
    }

    /**
     * 获取左孩子节点
     *
     * @param parentIndex
     * @return
     */
    private int leftChildData(int parentIndex) {
        if (parentIndex < 0) {
            return -1;
        }
        int leftChildIndex = parentIndex * 2 + 1;
        if (leftChildIndex > (this.count - 1)) {
            return -1;
        }
        return this.heapArray[leftChildIndex];
    }

    /**
     * 获取右孩子节点
     *
     * @param parentIndex
     * @return
     */
    private int rightChildData(int parentIndex) {
        if (parentIndex < 0) {
            return -1;
        }
        int rightChildIndex = parentIndex * 2 + 2;
        if (rightChildIndex > (this.count - 1)) {
            return -1;
        }
        return this.heapArray[rightChildIndex];
    }


    /**
     * 为了节省时间,不想单独写类,借助已有的方法，对数组进行堆化
     * @param targetArray
     * @return
     */
    public int[] heapTransfer(int [] targetArray ){
        //step1:将要堆化的数组值，复制给堆对象的数组,并更新count属性
        for(int i=0;i<targetArray.length;i++){
            this.heapArray[i]=targetArray[i];
            this.count=targetArray.length;
        }

        //step2:循环遍历，从最后一个父亲节点向下调整，直到父亲节点是根节点为至
        int lastParentIndex=((this.count-1)-1)/2;
        for(int i=lastParentIndex;i>=0;i--){
            downSift(i);
        }

        //step3:返回结果
        return this.heapArray;
    }


    public static void main(String[] args) {
        MinHeap minHeap =new MinHeap(10);
        minHeap.addData(7);
        minHeap.addData(6);
        minHeap.addData(5);
        minHeap.addData(4);
        minHeap.addData(3);
        minHeap.addData(2);
        minHeap.addData(1);

        System.out.println(Arrays.toString(minHeap.heapArray));

        int data = minHeap.pullData();
        System.out.println("取出元素="+data +"剩余列表="+Arrays.toString(minHeap.heapArray));
        int data1 = minHeap.pullData();
        System.out.println("取出元素="+data1 +"剩余列表="+Arrays.toString(minHeap.heapArray));



        //进行堆化
        int[] target={10,9,5,7,5,6,4,3,2,1};
        int[] result=minHeap.heapTransfer(target);
        System.out.println("堆化后的数组=>"+Arrays.toString(result));


    }
}

8、桶排序

9、选择排序

 

二、查找类

1、一个数组中的数据呈山峰状，比如：[1,2,3,17,16,15,14]，或[1,2,3,4,5] ,或[6,5,4,3,2]。快速找到最大数。

public class BinarySearch {

    public static void main(String[] args) {
        int[] array = {1, 2, 3, 4, 5, 19, 18, 17, 16, 15, 14, 13, 12};
        int[] array1 = {18, 15, 14, 13};
        int[] array2 = {10, 14, 15, 16};
        System.out.println(queryMaxByBinary(array1));
    }


    private static int queryMaxByBinary(int[] array) {
        int length = array.length;
        return queryMaxByBinary(array, 0, length - 1);

    }

    /**
     * 二分查找最大数
     *
     * @param array
     * @param beginIndex
     * @param endIndex
     * @return
     */
    private static int queryMaxByBinary(int[] array, int beginIndex, int endIndex) {
        int midIndex = mid(beginIndex, endIndex);
        int leftData = leftData(array, midIndex);
        int rightData = rightData(array, midIndex);
        int midData = array[midIndex];
        if (midData >= leftData && midData >= rightData) {
            return midData;
        } else if (midData < rightData) {
            return queryMaxByBinary(array, midIndex + 1, endIndex);
        } else if (midData < leftData) {
            return queryMaxByBinary(array, beginIndex, midIndex - 1);
        }
        return -1;
    }

    /**
     * 获取左侧数据
     *
     * @param array
     * @param midIndex
     * @return
     */
    private static int leftData(int[] array, int midIndex) {
        if (midIndex == 0) {
            return array[midIndex];
        }
        return array[midIndex - 1];
    }

    /**
     * 获取右侧数据
     *
     * @param array
     * @param midIndex
     * @return
     */
    private static int rightData(int[] array, int midIndex) {
        if (midIndex == (array.length - 1)) {
            return array[midIndex];
        }
        return array[midIndex + 1];
    }

    /**
     * 求中位数
     *
     * @param beginIndex
     * @param endIndex
     * @return
     */
    private static int mid(int beginIndex, int endIndex) {
        return (beginIndex + endIndex) / 2;
    }
}

2、使用二分法查找一个数组中的指定数（二分查找，数组中的数据需要有序）

public class TestBinarySearch {


    public static void main(String[] args) {

        int[] a = {1, 2, 3, 5, 8, 9, 10};
        System.out.println(queryArrayIndexByBinary(a, 4));
    }


    public static int queryArrayIndexByBinary(int[] array, int data) {
        return queryArrayIndexByBinary(array, data, 0, array.length - 1);
    }

    public static int queryArrayIndexByBinary(int[] array, int data, int beginIndex, int endIndex) {
        if(data<array[beginIndex] || data>array[endIndex] || beginIndex>endIndex){
            //数据小于最左数据 || 数据大于最右数据 || 左下标大于右下标 都表示数据不存在
            return -1;
        }
        int midIndex = mid(beginIndex, endIndex);
        int midData = array[midIndex];

        if (midData > data ) {
            //如果向数组左端查找,则中间坐标-1
            return queryArrayIndexByBinary(array, data, beginIndex, midIndex-1);
        } else if (midData < data) {
            //如果向数组右端查找,则中间坐标+1
            return queryArrayIndexByBinary(array, data, midIndex+1, endIndex);
        }
        return midIndex;
    }

    /**
     * 求中位数
     *
     * @param beginIndex
     * @param endIndex
     * @return
     */
    private static int mid(int beginIndex, int endIndex) {
        return (beginIndex + endIndex) / 2;
    }
}

 

 

三、计算类

1、求出数组中最大连续元素的和 

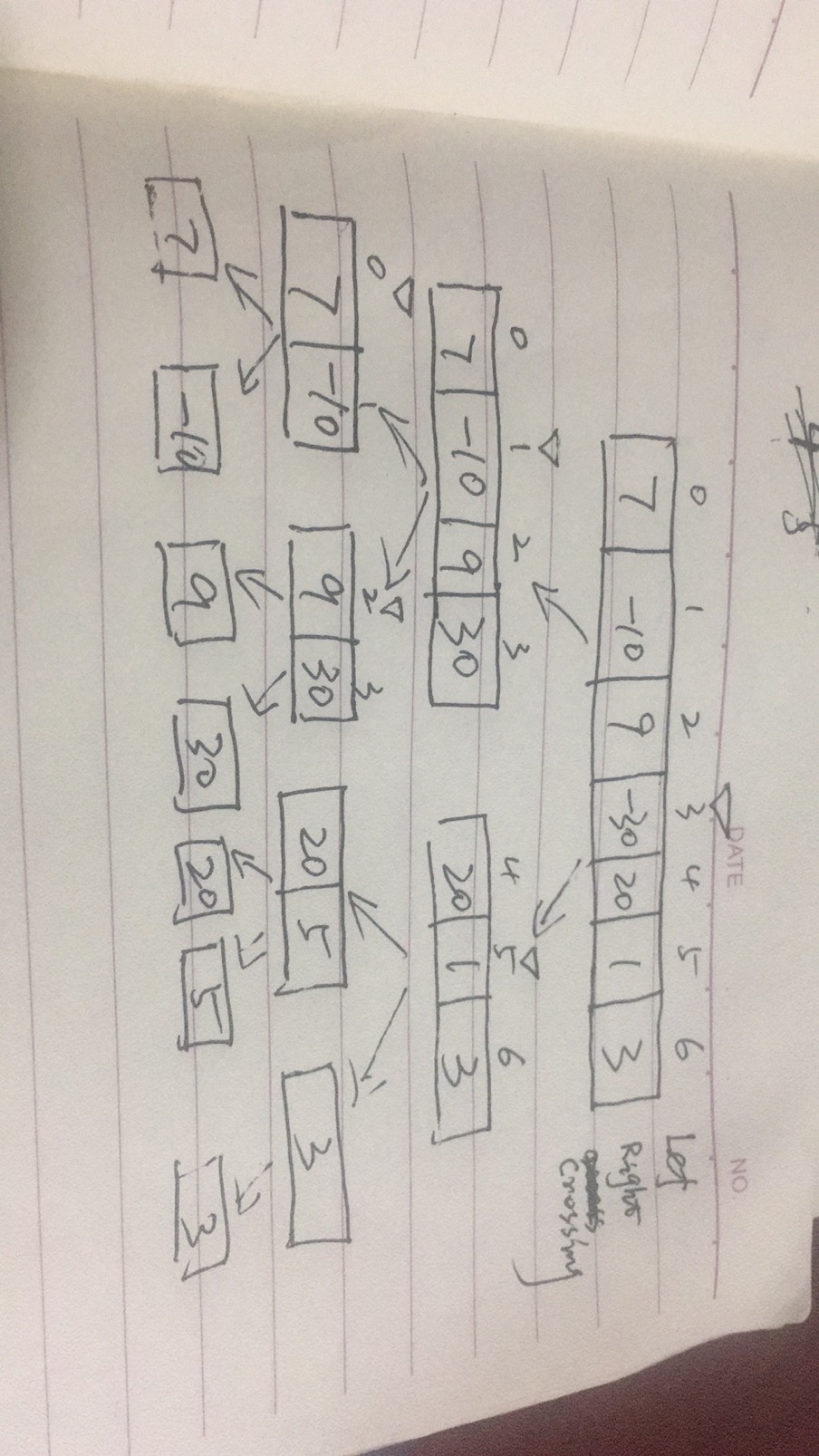
public class MaxSumArrayTest {

    /**
     * 最大子数组的计算
     * 前提：数组中需要有负数出现
     *
     * @param args
     */
    public static void main(String[] args) {
        int[] array={7,-10,9,-30,20,1,3};
        MaxSumResult maxSumResult= queryMaxSumArray(array);
        System.out.println("最大子数组之和为=>"+maxSumResult.getSum());
        System.out.println("起始下标=>"+maxSumResult.getBeginIndex());
        System.out.println("结束下标=>"+maxSumResult.getEndIndex());
    }


    public static MaxSumResult queryMaxSumArray(int[] array) {
       return  querySubArray(array,0,array.length-1);
    }


    /**
     * 求出最大子数组
     *
     * @param array
     * @param beginIndex
     * @param endIndex
     * @return
     */
    public static MaxSumResult querySubArray(int[] array, int beginIndex, int endIndex) {
        //起始坐标和结束坐标相等，表示为只有一个元素的子数组，其最大子数组就是本身
        if (beginIndex == endIndex) {
            MaxSumResult result = new MaxSumResult();
            result.setBeginIndex(beginIndex);
            result.setEndIndex(beginIndex);
            result.setSum((double) array[beginIndex]);
            return result;
        }

        //求出数组的中点
        int midIndex = midIndex(beginIndex, endIndex);

        //step1:求出左侧子数组的最大子数组
        MaxSumResult leftArrayResult=querySubArray(array,beginIndex,midIndex);

        //step2:求出右侧子数组的最大子数组
        MaxSumResult rightArrayResult=querySubArray(array,midIndex+1,endIndex);

        //step3:求出跨越数组中点的最大子数组
        MaxSumResult crossingArrayResult=queryMaxCrossingMidArray(array,beginIndex,midIndex,endIndex);

        //step4:从中选择最大子数组的结果
        if(leftArrayResult.getSum()>rightArrayResult.getSum() && leftArrayResult.getSum()>crossingArrayResult.getSum()){
            //左侧子数组的最大子数组之和大于右侧子数组的最大子数组之和  并且 大于跨越中点的子数组的最大子数组之和
            return leftArrayResult;
        }else if(rightArrayResult.getSum()>leftArrayResult.getSum() && rightArrayResult.getSum()>crossingArrayResult.getSum()){
            //右侧子数组的最大子数组之和大于最侧子数组的最大子数组之和  并且 大于跨越中点的子数组的最大子数组之和
            return rightArrayResult;
        }else{
            //跨越中点的最大子数组之和大于最侧和右侧的子数组的结果
            return crossingArrayResult;
        }

    }


    /**
     * 找出跨越中点的最大子数组结果
     *
     * @param array
     * @param beginIndex
     * @param midIndex
     * @param endIndex
     * @return
     */
    public static MaxSumResult queryMaxCrossingMidArray(int[] array, int beginIndex, int midIndex, int endIndex) {
        //step1:从中点求出向左的最大子数组信息
        Double maxLeftSum=Double.NEGATIVE_INFINITY;
        Double leftCurrentSum=0D;
        int maxLeftIndex=-1;
        for(int i=midIndex;i>=beginIndex;i--){
            leftCurrentSum+=array[i];
            if(leftCurrentSum>maxLeftSum){
                maxLeftSum=leftCurrentSum;
                maxLeftIndex=i;
            }
        }

        //step2:从中点向右求出最大子数组信息
        Double maxRightSum=Double.NEGATIVE_INFINITY;
        Double rightCurrentSum=0D;
        int maxRightIndex=-1;
        for(int i=midIndex+1;i<=endIndex;i++){
            rightCurrentSum+=array[i];
            if(rightCurrentSum>maxRightSum){
                maxRightSum=rightCurrentSum;
                maxRightIndex=i;
            }
        }
        MaxSumResult maxSumResult=new MaxSumResult();
        maxSumResult.setBeginIndex(maxLeftIndex);
        maxSumResult.setEndIndex(maxRightIndex);
        maxSumResult.setSum(maxLeftSum+maxRightSum);
        return maxSumResult;
    }

    /**
     * 求出中点
     * @param beginIndex
     * @param endIndex
     * @return
     */
    public static int midIndex(int beginIndex, int endIndex) {
        return (beginIndex + endIndex) / 2;
    }


}


/**
 * 计算结果
 */
class MaxSumResult {
    /**
     * 起始下标
     */
    private int beginIndex;
    /**
     * 结束下标
     */
    private int endIndex;
    /**
     * 最大和
     */
    private Double sum;

    public int getBeginIndex() {
        return beginIndex;
    }

    public void setBeginIndex(int beginIndex) {
        this.beginIndex = beginIndex;
    }

    public int getEndIndex() {
        return endIndex;
    }

    public void setEndIndex(int endIndex) {
        this.endIndex = endIndex;
    }

    public Double getSum() {
        return sum;
    }

    public void setSum(Double sum) {
        this.sum = sum;
    }
}