【数据结构和算法】红黑树
参考资料:https://www.cnblogs.com/skywang12345/p/3245399.html
https://www.cnblogs.com/wll-cs/p/5640266.html
https://www.cnblogs.com/yinbiao/p/10732600.html
一、红黑树的特性
性质五:从任一节点到其没个叶节点的所有路径都包含相同数目的黑色节点;
二、红黑树的旋转操作
红黑树的基本操作是添加和删除,在对红黑树进行添加和删除之后,都会用到旋转方法,为什么呢?道理很简单,因为添加或者删除红黑树中的结点之后,红黑树就发生了变化,可能不满足上面的5条性质了,这个时候就需要通过旋转操作来保证它依旧是一棵红黑树,旋转分为左旋和右旋
(旋转操作仅仅只是用来调节结点的位置的,就是为了满足红黑树的性质5)
1.左旋
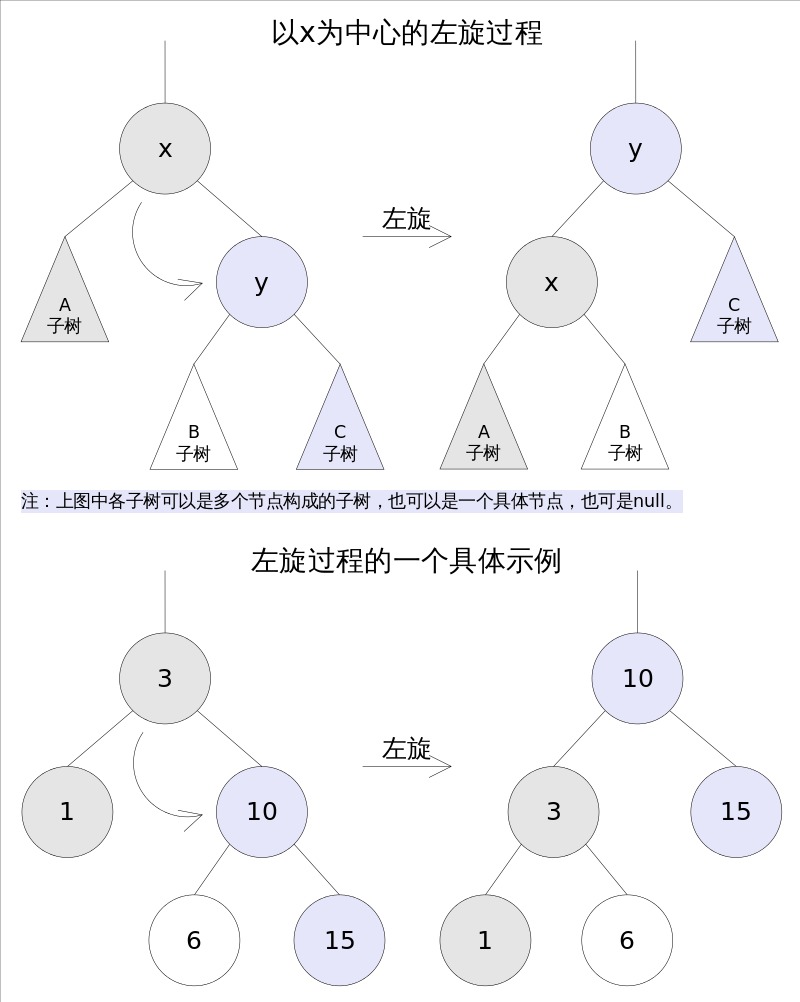
2.右旋
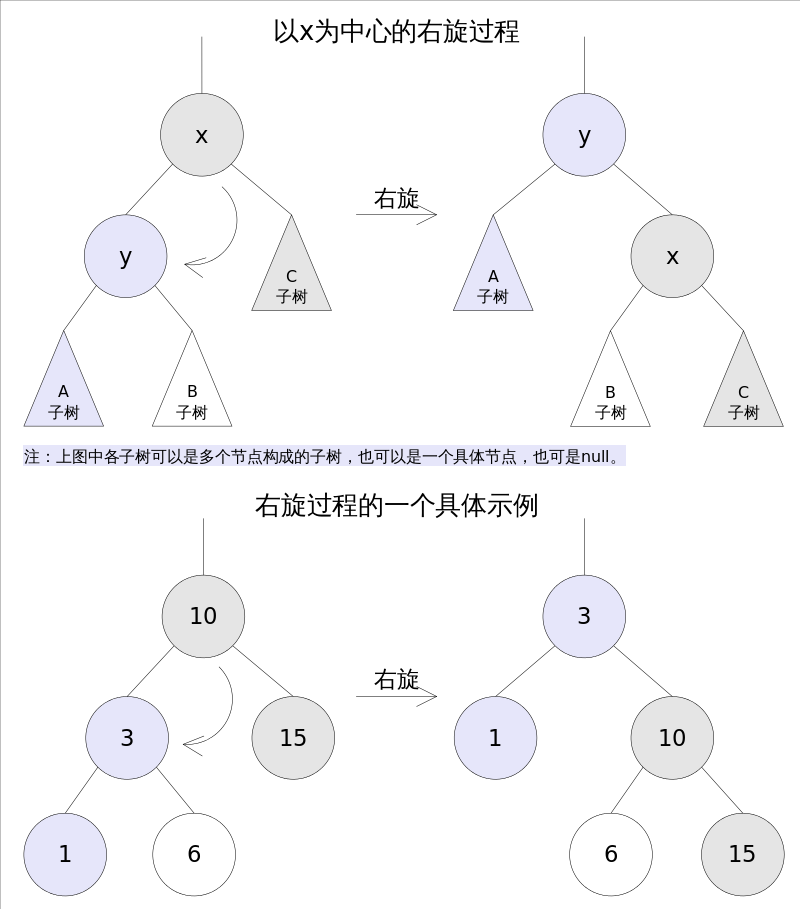
三、红黑树的节点插入
添加操作宏观过程:首先将红黑树当作一颗查找树一样将结点插入,然后将结点着为红色,最后通过旋转和重新着色的方法使之重新成为红黑树
将新加入的结点涂成红色的原因:
1)不违背红黑树的性质5:从任意一个结点出发到空叶子结点,经过的黑色结点个数相同
2)按照红黑树的性质4我们知道红黑树中黑结点的个数至少是红结点个数的两倍,所以新增结点的父亲结点是黑结点的概率比较大,如果新增结点的父节点为黑色,那么此时不需要再去进行任何调整操作,因此效率很高,所以新结点应该涂成红色
少违背一条性质,意味着我们后续的旋转和重新着色操作会简单很多
现在我们来看看新增一个红色的结点会违背红黑树的5条性质中的哪些?
1)每个结点或红或黑 2)根结点是黑色 3)空叶子结点是黑色 4)如果一个结点是红色,那么它的子节点是黑色 5)从任意一个结点出发到空的叶子结点经过的黑结点个数相同
1.显然没有违背
2.根据查找树的特定,插入操作不好改变根结点,所以也没有违背
3.插入的肯定不是空叶子结点,所以也没有违背
4.有可能违背!!!
5.插入结点涂成红色就是为了不违背第5条性质
现在我们来分析一下新增的结点(红色)插入之后可能面临的几种情况,以及他们的处理措施
1.插入的结点为根结点
将新插入的红色结点变成黑色结点,满足根结点为黑色结点的要求!
2.父亲结点为黑色结点
这个时候不需要进行任何调整操作,此时的树仍然是一颗标准的红黑树
3.父亲结点为红色结点的情况下,叔叔结点为红色结点(不用考虑左右)
解决方案:将叔叔和父亲结点改为黑色,爷爷结点改为红色,未完
然后又将爷爷结点当作插入结点看待,一直重复从1开始节点属性和颜色的检查,并进行相应的操作(有可能是需要继续进行3的操作,也有可能直接退出,也有可能需要旋转进行节点调整),直到当前结点为根结点,然后将根结点变成黑色。
示例:
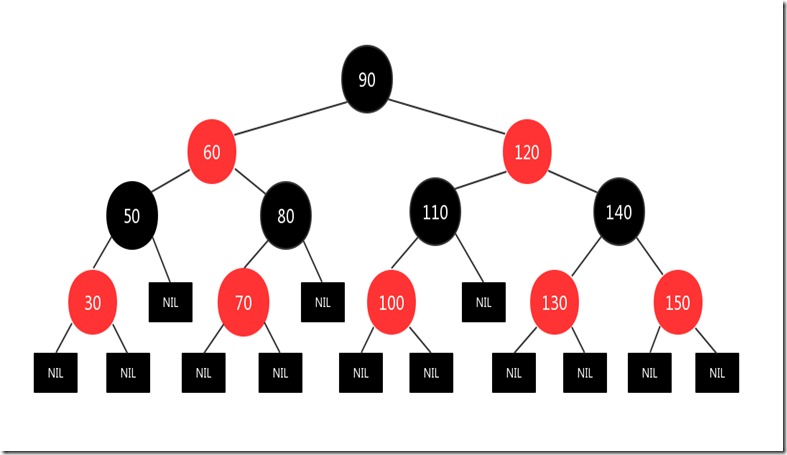
插入一个125的结点:
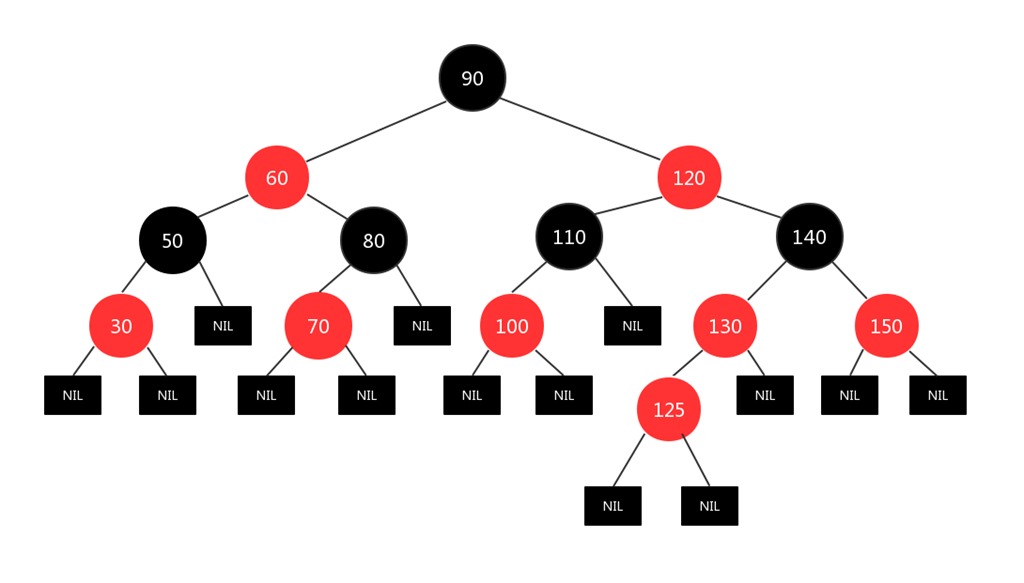
现在125结点和130结点都是红色的,显然违背了规则4,所以将新插入结点的父亲130结点和插入结点的叔叔结点150变成黑色,并将新插入结点的爷爷结点140变成红色,图如下:
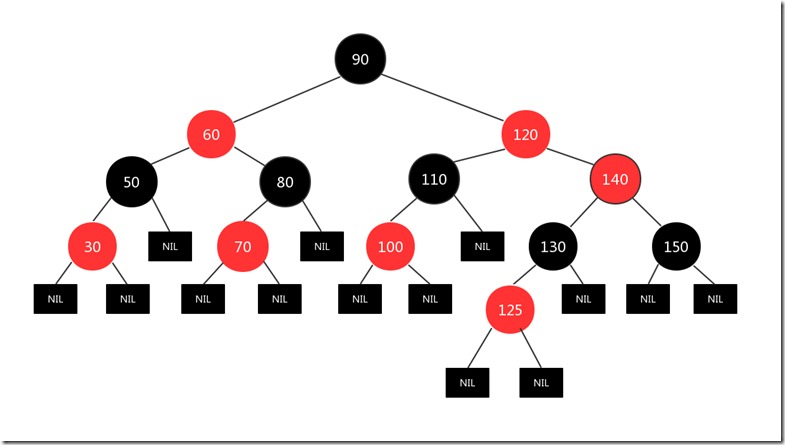
然后又将140结点当作新插入结点处理(因为140结点和新插入结点面临的情况都是一样的:和父亲结点都是红色),也就是做如下处理:将140结点的父亲结点120和140的叔叔结点60变成黑色结点,将140结点的爷爷结点变成红色,因为遍历到了根结点,要满足根结点是黑色的性质要求,所以又将140的爷爷结点也就是根结点变成黑色,图如下:
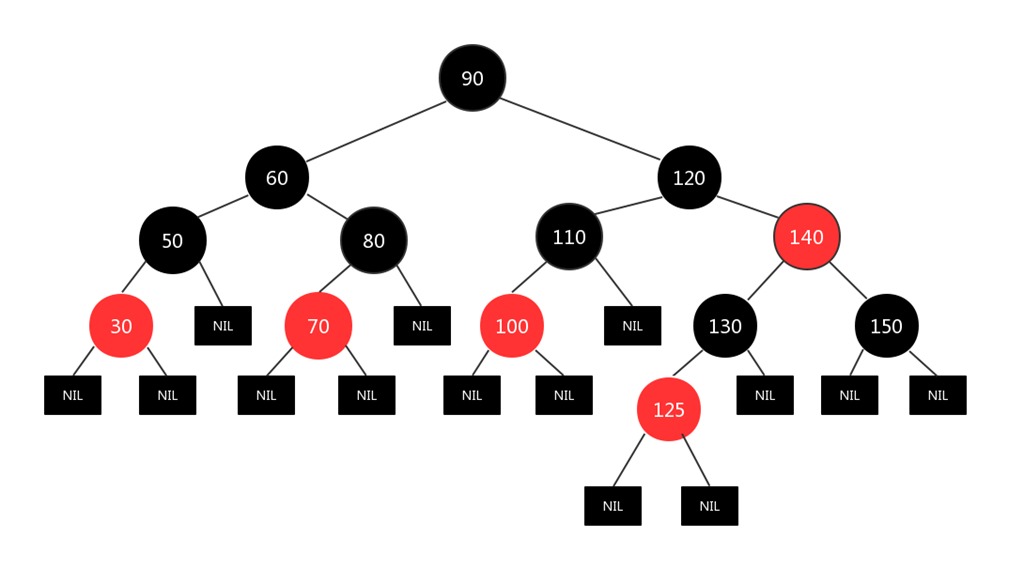
到这里,为新插入结点125所做的某些结点重新着色的操作就完成了,现在该树是标准的红黑树了!
4.新插入的结点的父亲结点为红色,其叔叔结点为黑色
1)父亲结点为爷爷结点的左孩子,新插入结点为父节点的左孩子(左左情况)
2)父亲结点为爷爷结点的右孩子,新插入结点为父亲结点的右孩子(右右情况)
上述两种情况都是同一个处理办法
比如下图,新插入结点为25,其父亲结点30为红色,其叔叔结点为空黑色叶子结点,且新插入结点和其父节点都是左孩子:
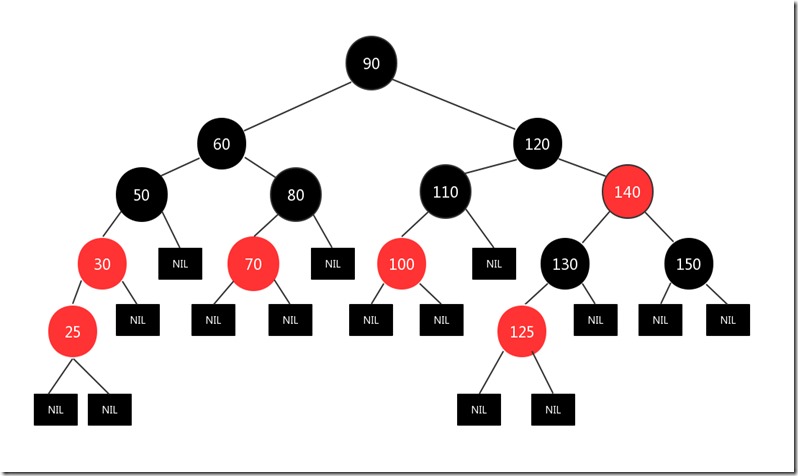
我们将其父亲结点和爷爷结点颜色互换,然后针对爷爷结点进行一次右旋(子和父的关系为:左左=>右旋,右右=>左旋),图如下:
现在这颗树完全满足红黑树的5个性质了(最好自己对照5个性质看一下)
现在又一个问题,我们为什么要进行旋转?
假设我们只将新增结点的父亲结点和其爷爷结点的颜色互换了,图如下:

我们发现上述两条到叶子结点的路径经过的黑色结点数量不一样!!!,所以它不满足红黑树的第5条性质,所以这就是我们旋转的意义所在!!!(因为无论你这么旋转都没有改变结点颜色,改变的是结点的位置,而这位置改变刚好能使得树满足红黑树的第5条性质!)
5.新插入的结点的父亲结点是红色,其叔叔结点是黑色
1)插入结点是右结点,父节点是左结点
2)插入结点是左结点,父亲结点是右结点
上述两种情况都是同一个处理办法
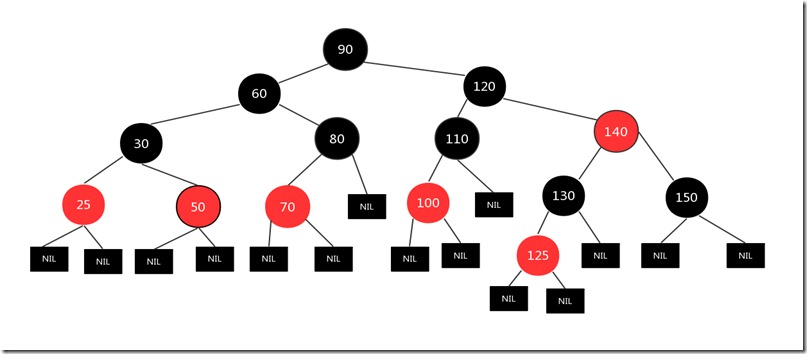
比如下图,新插入结点是126,其父结点125为红色,其叔叔结点为空的黑色结点,而且插入结点是右结点,父结点是左结点
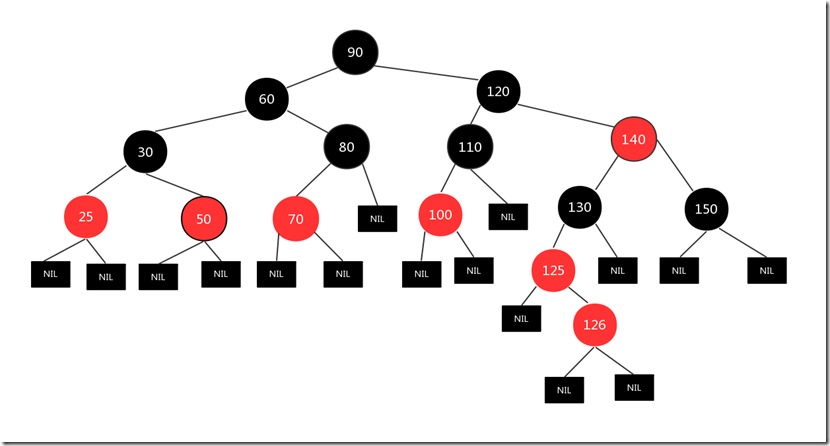
我们将父亲结点125看作当前结点进行左旋,旋转结果如下:
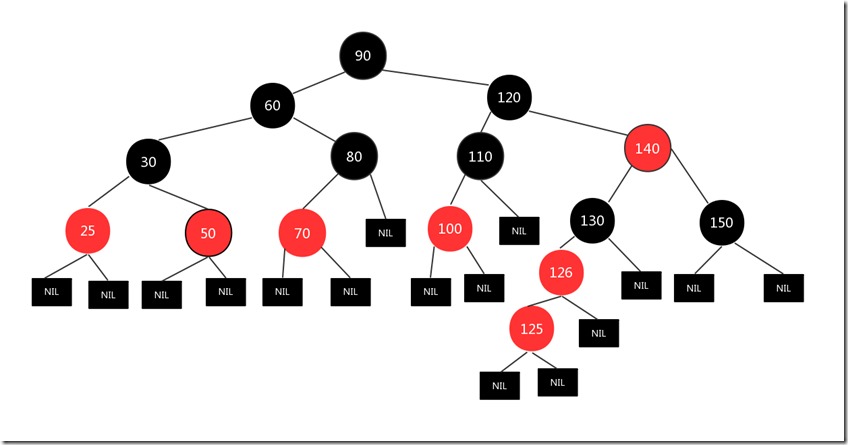
现在我们的当前结点是125,现在125的处境和上面的情况4是一样的(父节点为红,叔叔结点为黑,插入结点为左结点,父亲结点也为左孩子)现在我们继续按照情况4的处理办法处理上述情况(措施和情况4一样,父亲结点和爷爷结点互换颜色,然后针对爷爷结点进行右旋(左左=>右旋 右右=>左旋)),处理后情况如下:
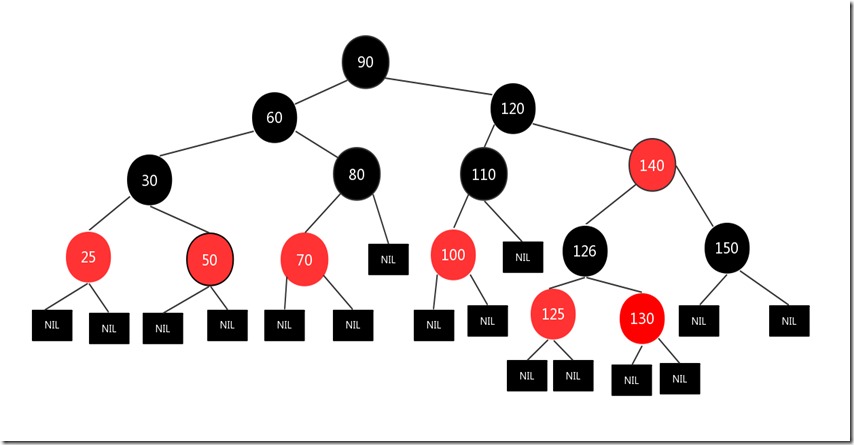
现在树就是一颗标准的红黑树了!
我们现在总结一下插入结点面临的几种情况以及采取的措施:
1.树为空,插入的结点为根结点 直接将插入的结点变成黑色 2.父亲结点为黑色结点 不需要任何操作 3.父亲结点为红色结点的情况下: 3.1 叔叔结点也为红色结点 将叔叔和父亲结点改为黑色,爷爷结点改为红色,未完,然后又将爷爷结点当作插入结点看待,一直进行上 面的操作,直到当前结点为根结点,然后将根结点变成黑色 3.2 叔叔结点为黑色结点的情况下: 3.2.1 (父亲结点为左孩子,插入结点也为左孩子)||(父亲结点为右孩子,插入结点也为右孩子) 将父亲结点和爷爷结点的颜色互换,然后针对爷爷结点进行一次旋转 3.2.2 (父亲结点为左孩子,插入结点为右孩子)||(父亲结点为右孩子,插入结点为左孩子) 针对父结点进行旋转,此时旋转后的情况必定是3.2.1的情况,然后按照3.2.1的情况处理
====================TreeMap中对于节点变色和旋转的代码如下===================================
代码的调整逻辑完全符合上述分析的逻辑

/** From CLR *X为当前红黑树最新插入的节点 */ private void fixAfterInsertion(Entry<K,V> x) { x.color = RED; //当前节点x不是空,也不是根节点,且x的父亲节点颜色为红色,才需要进行调整(若x为根节点或x节点的父亲节点颜色为黑色,则说明调整完成) while (x != null && x != root && x.parent.color == RED) { //x的父亲节点自身为左节点的情况 if (parentOf(x) == leftOf(parentOf(parentOf(x)))) { //找到x节点的叔叔节点y Entry<K,V> y = rightOf(parentOf(parentOf(x))); //如果叔叔节点和父亲节点为红色,则将叔叔和父亲变为黑色,爷爷变为红色,将爷爷节点当做新插入节点,继续下一轮调整 if (colorOf(y) == RED) { setColor(parentOf(x), BLACK); setColor(y, BLACK); setColor(parentOf(parentOf(x)), RED); x = parentOf(parentOf(x)); } else { //父亲节点为红色,叔叔节点为黑色的情况 if (x == rightOf(parentOf(x))) { //父亲节点为左节点,当前节点为右节点,对将父亲节点作为当前节点,然后进行一次左旋。让其成为左左的情况, x = parentOf(x); rotateLeft(x); } //当前节点为左节点,父亲节点为左节点,父亲节点为红色,叔叔节点为黑色。则将父亲节点变黑,爷爷节点变红,对爷爷节点进行一次右旋 setColor(parentOf(x), BLACK); setColor(parentOf(parentOf(x)), RED); rotateRight(parentOf(parentOf(x))); } } else { //x的父亲节点自身为右节点的情况 //x的叔叔节点,其叔叔节点为左节点 Entry<K,V> y = leftOf(parentOf(parentOf(x))); if (colorOf(y) == RED) { //x的父亲节点和叔叔节点都为红色,则将父亲节点和叔叔节点颜色变成黑色,爷爷节点变成红色,将爷爷节点作为当前节点,继续调整 setColor(parentOf(x), BLACK); setColor(y, BLACK); setColor(parentOf(parentOf(x)), RED); x = parentOf(parentOf(x)); } else { //x的父亲节点为红色,叔叔节点为黑色的情况 if (x == leftOf(parentOf(x))) { //x自己为左节点,x的父亲为右节点,将父亲节点做未当前节点,进行一次右旋操作,让其成为右右的情况 x = parentOf(x); rotateRight(x); } // 当前节点为右节点,父亲节点为右节点,父亲节点为红色,叔叔节点为黑色。将爷爷节点变为红色,父亲节点为黑色,对爷爷节点进行一次左旋。 setColor(parentOf(x), BLACK); setColor(parentOf(parentOf(x)), RED); rotateLeft(parentOf(parentOf(x))); } } } //因为节点在调整的过程中,退出时,再次将根节点的颜色设置为黑色 root.color = BLACK; }
四、红黑树的节点删除
先说一个删除结点的过程原理:首先将红黑树当作一个二叉查找树,将该结点从二叉查找树种删除,然后通过一些列重新着色操作等一系列措施来修正该树,使之重新成为一颗红黑树
删除结点其实很容易,难的是如何使得删除结点后的树重新成为一个红黑树
我们可以根据删除结点N的儿子个数分为三种情况:
1.删除结点没有儿子
2.删除结点有1个儿子
3.删除结点有2个儿子
接下来我们又可以对以上三种情况继续进行细分
一.删除结点没有儿子的情况: 1)删除结点为红色 2)删除结点为黑色,其兄弟结点没有儿子 3)删除结点为黑色,其兄弟结点有一个孩子不空,并且该孩子为右孩子 4)删除结点为黑色,其兄弟结点有一个孩子不空,并且该孩子为左孩子 5)删除结点为黑色,其兄弟结点有两个孩子,而且兄弟结点为红色 6)删除结点为黑色,其兄弟结点有两个孩子,而且兄弟结点为黑色 二.删除结点只有一个儿子的情况: 1)删除结点为黑色,其唯一的儿子结点为红色(必定是红色,要不然不符合红黑树的第5条性质) 2)删除结点为红色,其儿子结点只能为黑:红黑树中不存在这种情况,要不然无法满足红黑树第5条性质 三.删除结点有两个儿子的情况:
现在我们就具体分析一下面临不同的操作到达该这么操作:
一.删除结点没有儿子的情况:
1)删除结点为红色
直接删除,比如下图,想要删除130结点
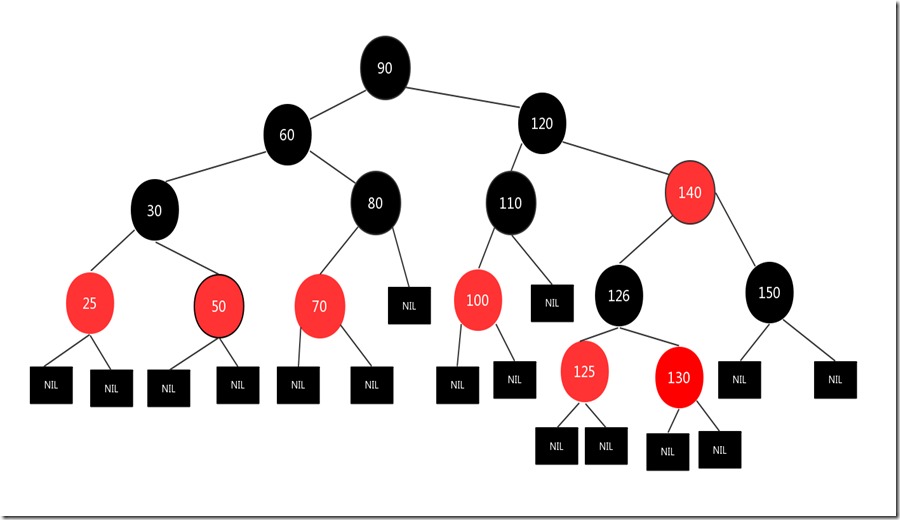
直接删除130结点,结果图如下:
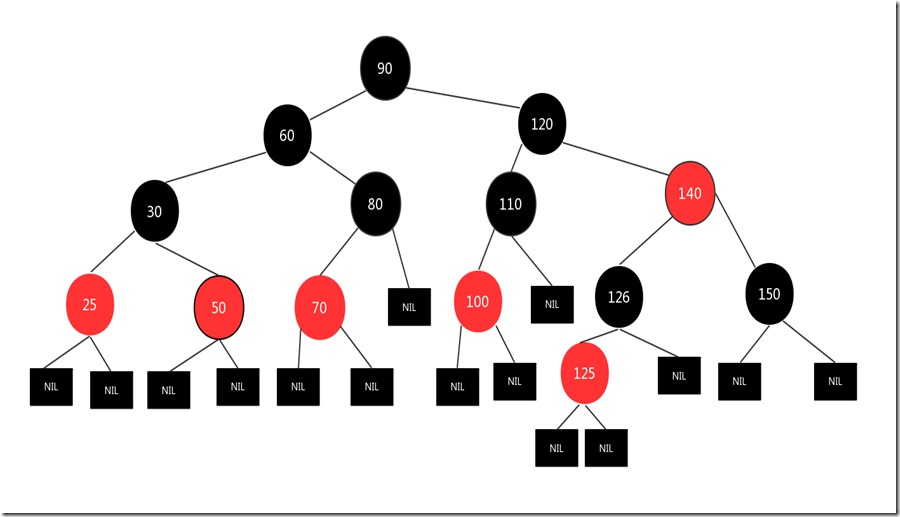
因为删除的是红色结点,不会影响红黑树第5条性质,所以可以直接删除
2)删除结点为黑色,其兄弟结点没有儿子
这种情况下其兄弟结点也肯定是黑色的(要满足红黑树第5条性质),假设现在要删除的是150这个结点,原图如下:
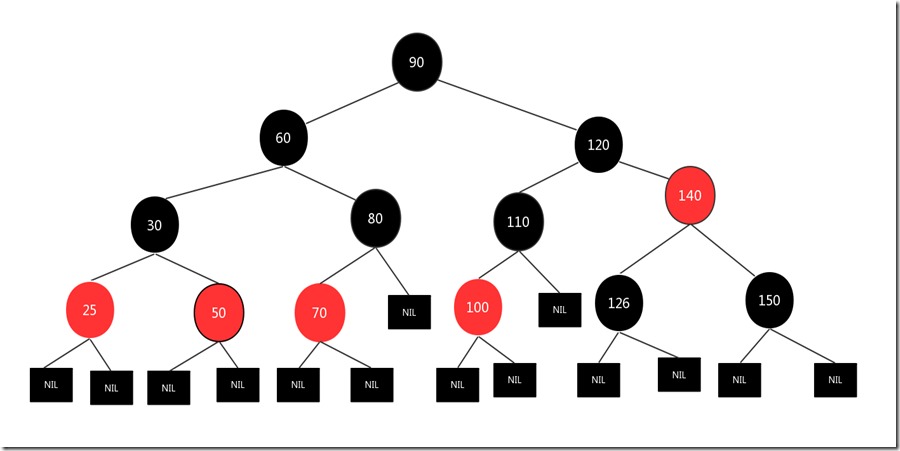
先删除结点150,然后将兄弟结点126变成红色,父亲结点140变成黑色,结果如下:
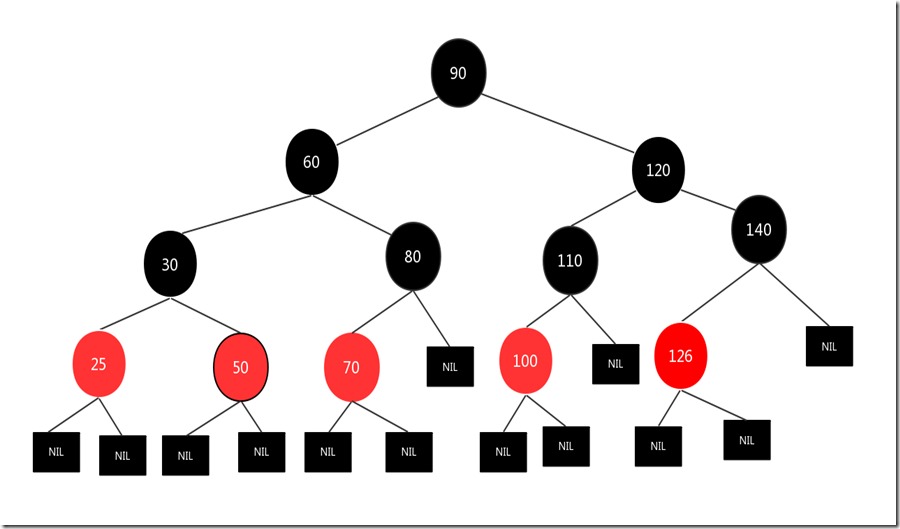
这样做的目的是为了满足红黑树的第5条性质,要不然根到最右边的叶子结点经过的黑色结点只有3个,而其他路径有4个
3)删除结点为黑色,其兄弟结点有一个孩子不空,并且该孩子和兄弟结点在同一边(同为左子树或者同为右子树)
假设现在要删除的结点为110,其兄弟结点140只有一个孩子150,而且都是右子树,满足上述条件,原图如下:
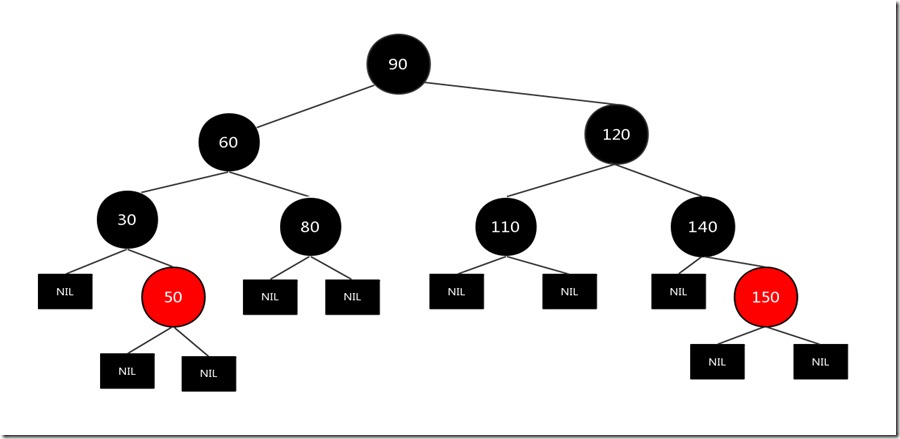
先把需要删除的结点110删除,然后这个时候需要交换兄弟结点140和父亲结点120的颜色,并且把父亲结点120涂成黑色,把兄弟结点的子节点150涂成黑色
1.如果兄弟结点和兄弟结点的儿子都在右子树的话:对父亲结点进行左旋
2.如果兄弟结点和兄弟结点的儿子都在左子树的话:对父亲结点进行右旋
上图是第一种情况,所以对父结点120进行左旋,结果如下:
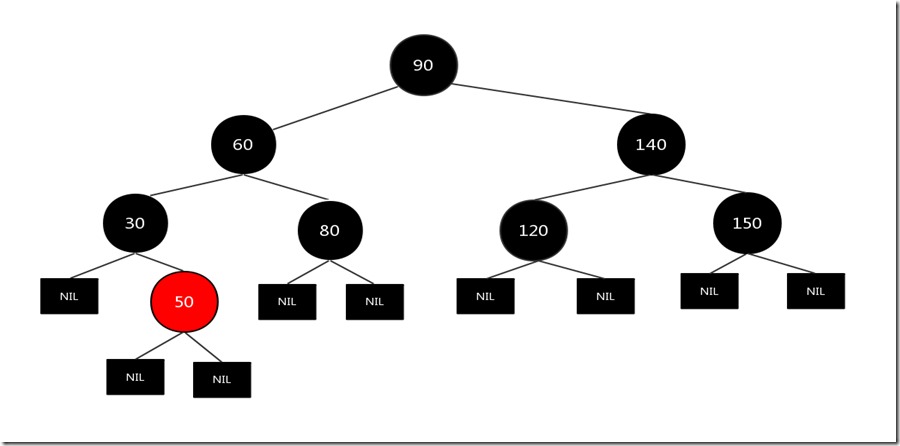
通过对某些结点重新着色和旋转,又将该树变成了一个标准的红黑树了
4)删除结点为黑色,其兄弟结点有一个孩子不空,并且该孩子和兄弟结点不在同一边(右左或者左右的情况)
(这种情况下,兄弟结点的儿子50结点只能为红色,要不然满足不了红黑树的第5条性质)
假设我们现在要删除的结点是80结点,其兄弟结点只有一个儿子,而且兄弟结点和兄弟结点的儿子是左右的情况(兄弟结点为左结点,兄弟结点的儿子为右结点),符合上述要求,原图如下:

现在我们先将需要删除的80结点删除,然后将兄弟结点和兄弟结点的儿子结点颜色互换
如果兄弟结点是左子树,兄弟结点的儿子结点是右子树:对兄弟结点进行左旋
如果兄弟结点是右子树,兄弟结点的儿子结点是左子树:对兄弟结点进行右旋
上图的情况是进行左旋,也就是对兄弟结点30进行左旋,结果如下图:
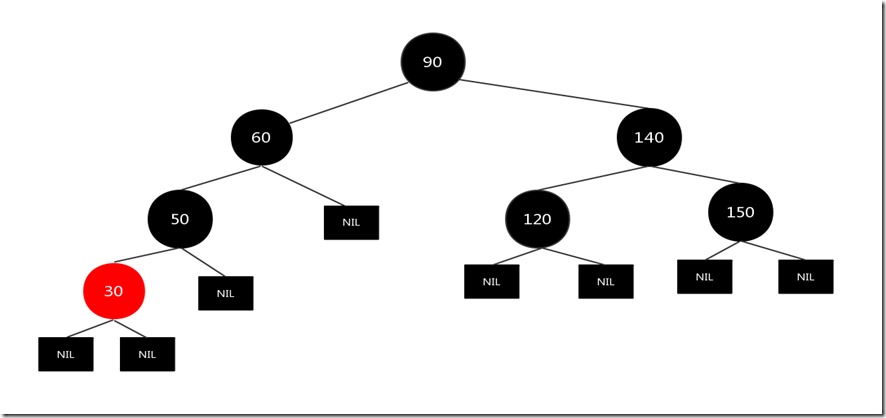
注意!!,现在还没有结束变换,我们发现变换之后的红黑树情况和情况3中的情况很相似,兄弟结点50和兄弟结点的子节点30处在同一边,我们可以按照情况3的处理办法进行处理:
交换兄弟结点50和父亲结点60的颜色,把父亲结点60和兄弟结点的子节点30涂成黑色
1.如果兄弟结点和兄弟结点的儿子都在右子树的话:对父亲结点进行左旋
2.如果兄弟结点和兄弟结点的儿子都在左子树的话,对父亲结点进行右旋
上图的情况是第2中,所以对父亲结点60进行右旋,结果如下:
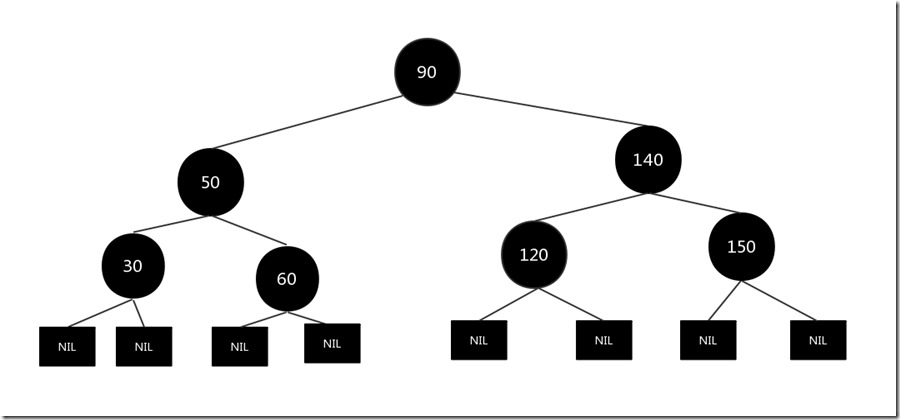
5)删除结点为黑色,其兄弟结点有两个孩子,兄弟结点为黑色而且两个孩子结点也为黑色
现在我们假设要删除的结点是130结点,其兄弟结点有两个孩子(可以把空的叶子结点看成黑色的儿子结点),而且兄弟结点和兄弟结点的儿子结点都是黑色,符合上述情况,原图如下:

先直接删除需要删除的结点130,然后将父亲结点140和兄弟结点150颜色互换即可,结果如下:
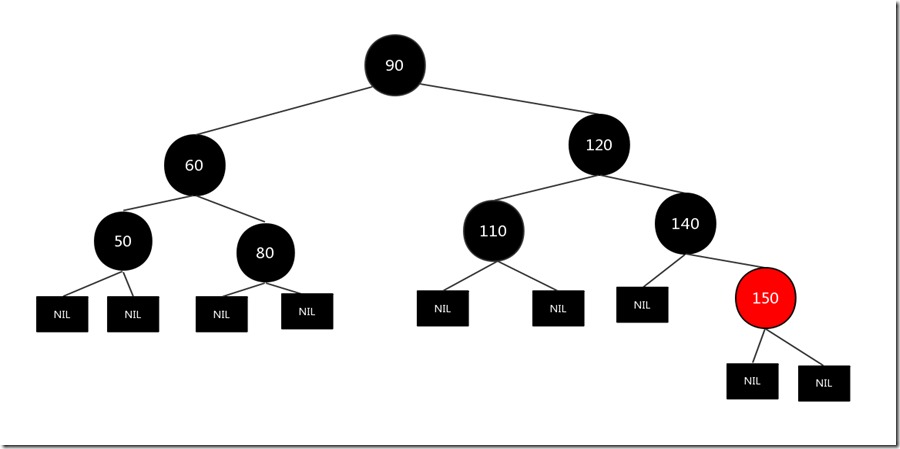
6)删除结点为黑色,其兄弟结点有两个孩子,而且兄弟结点为红色
假设我们要删除的结点是110,其兄弟结点140为红色而且有两个孩子,原图如下:
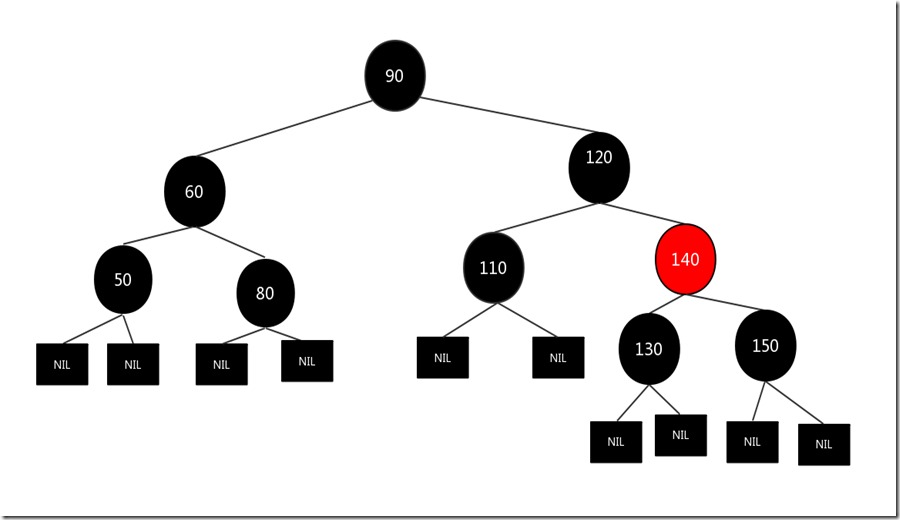
我们先交换兄弟结点140和父亲结点120的颜色
1.被删除的元素为左子树:对父亲结点左旋
2.被删除的元素为右子树:对父亲结点右旋
上图的情况是第一种情况,所以我们对父亲结点140进行左旋,按照上面操作之后(未完),结果如下:
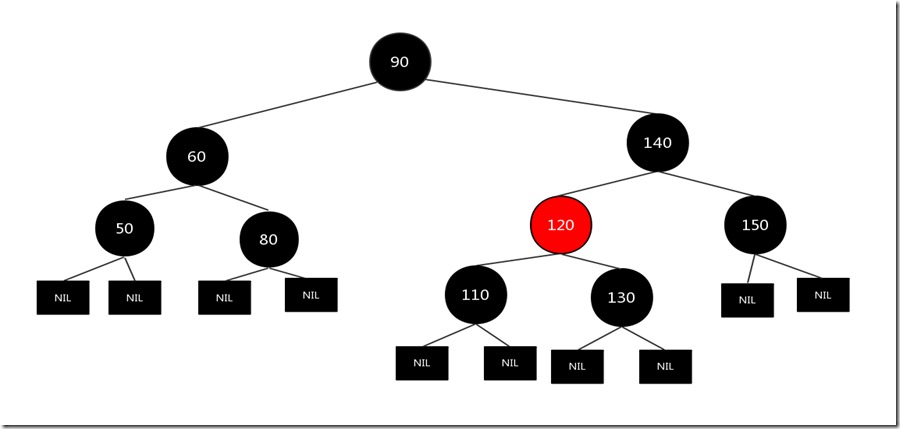
旋转完之后,我们发钱要删除的110节点,此时变成了:110的兄弟节点,没有孩子节点的情形。此时只需要将110节点删除,将120和130节点颜色进行互换即可。结果如下图:
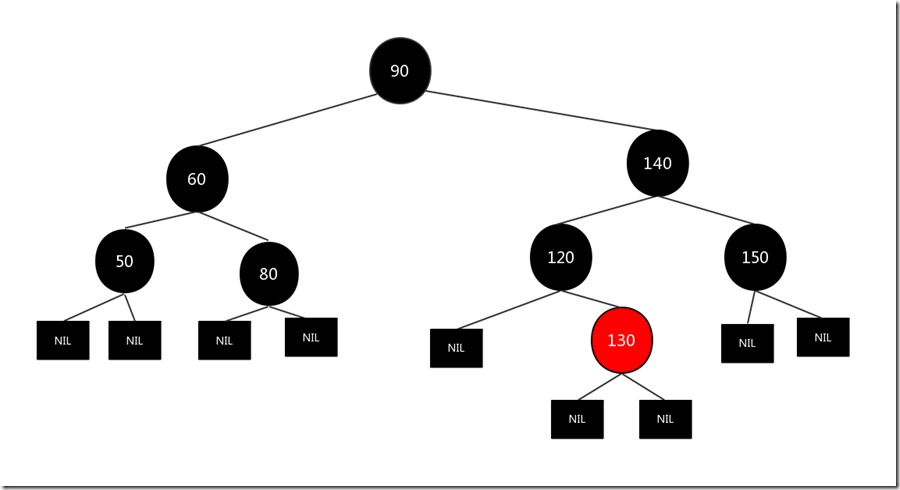
我们现在对删除结点没有儿子结点的6种删除情况进行一下总结:
删除结点没有儿子结点:
1)删除结点为红色: 直接删除 2)删除结点为黑色,其兄弟结点没有儿子: 兄弟结点变红,父亲结点变黑 3)删除结点为黑色,其兄弟结点有一个孩子不空,并且该孩子和兄弟结点在同一边(同为左子树或者同为右子树): 1.不管是括号中那种情况,先交换兄弟结点和父亲结点的颜色,并且把父亲结点和兄弟结点的子结点涂成黑色 2.1如果兄弟结点和兄弟结点的儿子都在右子树的话:对父亲结点进行左旋 2.2如果兄弟结点和兄弟结点的儿子都在左子树的话:对父亲结点进行右旋 4)删除结点为黑色,其兄弟结点有一个孩子不空,并且该孩子和兄弟结点不在同一边(右左或者左右的情况): 1.先将兄弟结点和兄弟结点的儿子结点颜色互换 2.1如果兄弟结点是左子树,兄弟结点的儿子结点是右子树:对兄弟结点进行左旋 2.2如果兄弟结点是右子树,兄弟结点的儿子结点是左子树:对兄弟结点进行右旋 3.将后续变换按照第3条处理 5)删除结点为黑色,其兄弟结点有两个孩子,兄弟结点为黑色而且两个孩子结点也为黑色: 1.将父亲结点和兄弟结点颜色互换 6)删除结点为黑色,其兄弟结点有两个孩子,而且兄弟结点为红色: 1.将兄弟结点和父亲结点的颜色互换 2.1 被删除的元素为左子树:对父亲结点左旋 2.2 被删除的元素为右子树:对父亲结点右旋 3.将后续变换按照第5条进行处理
以上6种情况讨论的都是删除结点没有儿子的情况(空叶子结点不算儿子结点)
现在我们来看看删除结点仅有一个儿子结点的情况!
二.删除结点仅有一个儿子结点的情况
1)删除结点为黑色,儿子结点无论左右都可以
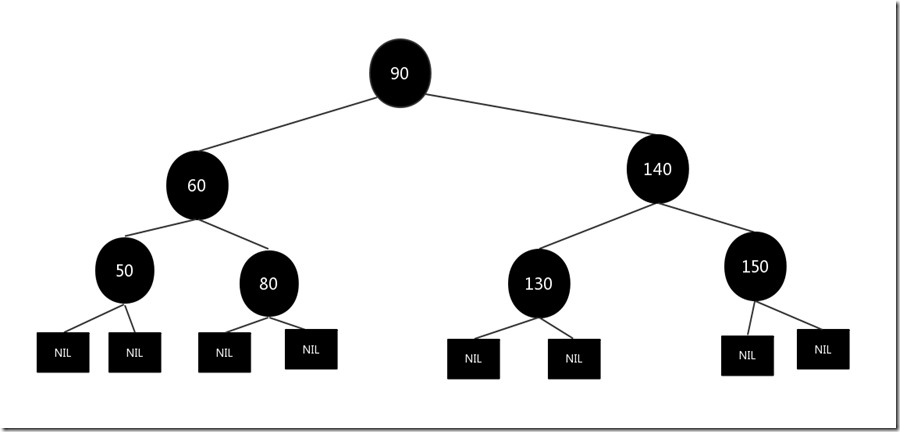
比如我们要删除的结点是120结点,删除结点为黑色,唯一的儿子结点130为红色(必须是红色,不然违背红黑树第5条性质)原图如下:

我们将需要删除的结点120删除,然后将子节点130涂黑放到被删除结点120的位置,结果如下:
2)删除结点为红色:其儿子结点只能为黑,红黑树中不存在这种情况,要不然无法满足红黑树第5条性质
总结一下删除结点只有一个儿子的情况:
1)删除结点为黑色,儿子结点无论左右都可以 将儿子结点涂成黑色放到被删除结点的位置
下面我们来看看删除结点有两个儿子结点的情况
三.删除结点有两个儿子结点
找到删除结点的右子树中最左的结点,两两值交换,然后删除结点的情况就变成了上面两种情况中的一种了
1.删除结点只有一个儿子的情况
2.删除结点没有儿子的情况
比如下图

假设要删除的结点是120,先找到结点120右子树中最左的结点125,交换两者的值,图如下:
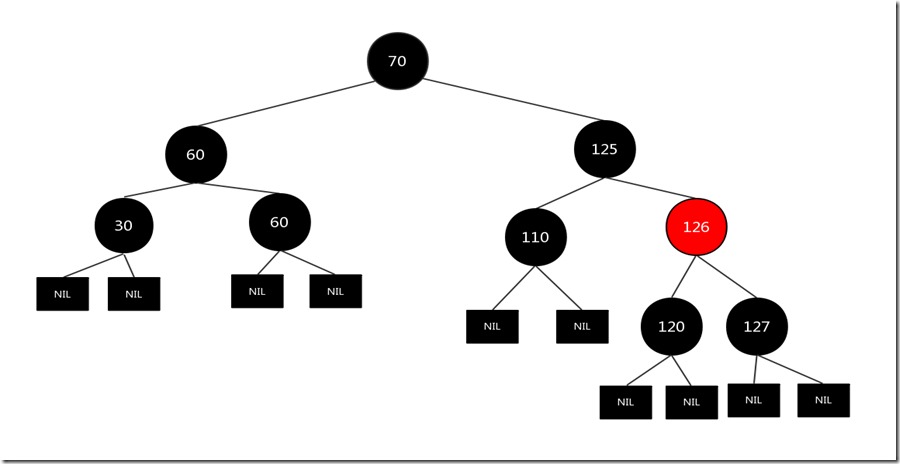
现在120仍然是要删除的结点,我们发现删除结点120没有一个儿子,而且其兄弟结点也没有儿子,那么其对应的情况为:
2)删除结点为黑色,其兄弟结点没有儿子: 兄弟结点变红,父亲结点变黑
经过上面的变形,结果如下:

经过变换,该树变成了一颗标准的红黑树
所以当删除结点右两个儿子结点的时候,我们只需要按照搜索二叉树的删除方法替换删除值,这样就可以将情况变成删除结点没有儿子结点或者1个儿子结点的情况处理了
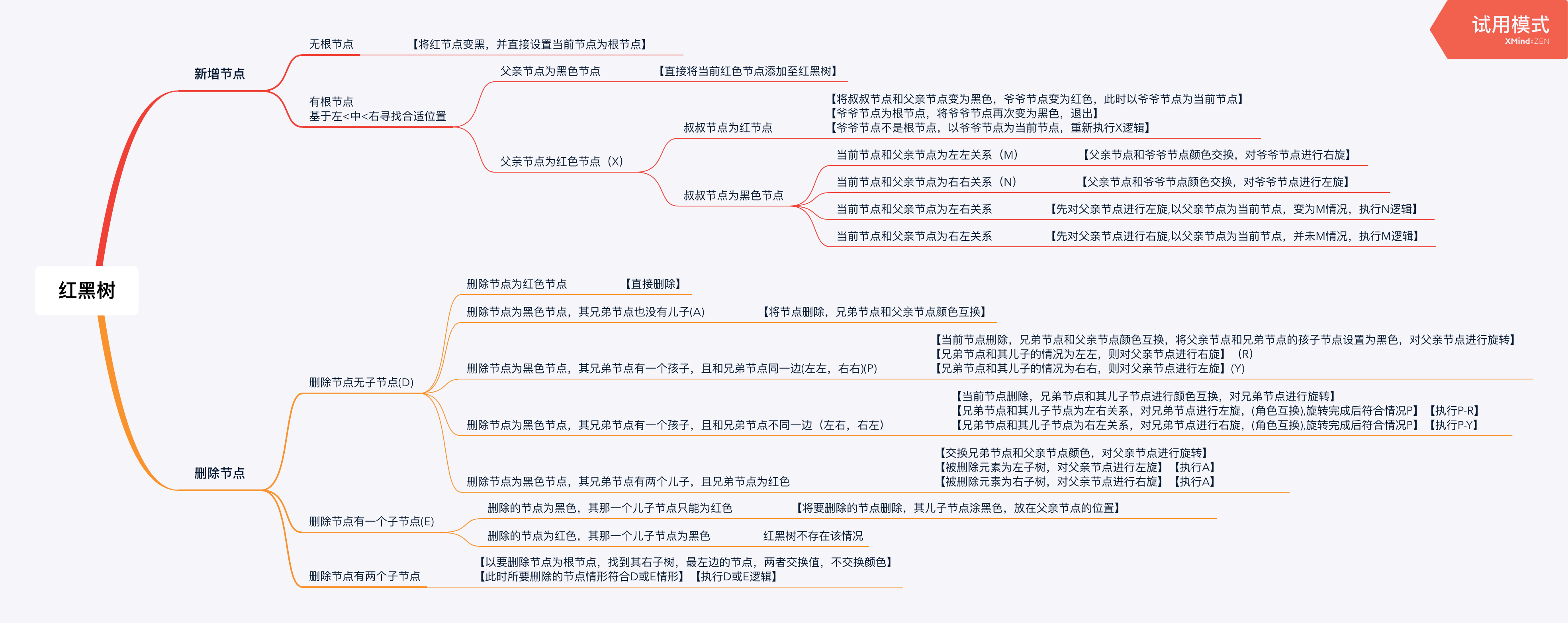
五、红黑树添加删除自平衡的执行逻辑