【算法和数据结构】漫画算法之树的遍历和二叉堆

一、树的遍历

树的的机构

   A

B     C

深度优先遍历顺序关注的是父节点的被遍历到的顺序。即A

• 前序遍历的顺序：A,B,C
• 中序遍历的顺序：B,A,C
• 后续遍历的顺序：B,C,A

 

 

         A

    B         C

D     E   F     G

 

广度优先遍历（层序遍历）的遍历顺序为：A,B,C,D,E,F,G

 

示例中的树的

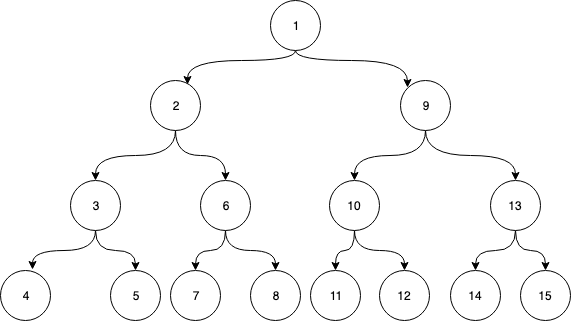
1、树的定义类

class TreeNode {
    private TreeNode leftTreeNode;
    private TreeNode rightTreeNode;
    private Integer nodeData;

    public TreeNode getLeftTreeNode() {
        return leftTreeNode;
    }

    public void setLeftTreeNode(TreeNode leftTreeNode) {
        this.leftTreeNode = leftTreeNode;
    }

    public TreeNode getRightTreeNode() {
        return rightTreeNode;
    }

    public void setRightTreeNode(TreeNode rightTreeNode) {
        this.rightTreeNode = rightTreeNode;
    }

    public Integer getNodeData() {
        return nodeData;
    }

    public void setNodeData(Integer nodeData) {
        this.nodeData = nodeData;
    }
}

2、树的遍历算法

import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;

public class TreeTraverseTest {


    public static void main(String[] args) {
        TreeNode treeNode = createTreeNode();
        //深度优先遍历测试
        //testDepthFirstTraversal(treeNode);
//        testDepthFirstTraversalByStack(treeNode);
        //广度优先遍历测试
        testBreadthFirstTraversal(treeNode);

    }


    /**
     * 递归实现深度优先遍历测试
     *
     * @param treeNode
     */
    public static void testDepthFirstTraversal(TreeNode treeNode) {
        //测试前序遍历，预期输出结果：1,2,3,4,5,6,7,8,9,10,11,12,13,14,15
        preOrderTraversalByRecursive(treeNode);

        //测试中序遍历，预期输出结果：4,3,5,2,7,6,8,1,11,10,12,9,14,13,15
        midOrderTraversal(treeNode);

        //测试后序遍历，预期输出结果：4,5,3,7,8,6,2,11,12,10,14,15,13,9,1
        afterOrderTraversal(treeNode);
    }


    /**
     * 利用栈进行深度优先遍历测试
     *
     * @param treeNode
     */
    public static void testDepthFirstTraversalByStack(TreeNode treeNode) {
        //测试前序遍历，预期输出结果：1,2,3,4,5,6,7,8,9,10,11,12,13,14,15
        preOrderTraversalByStack(treeNode);
        //测试中序遍历，预期输出结果：4,3,5,2,7,6,8,1,11,10,12,9,14,13,15
        midOrderTraversalByStack(treeNode);
        //测试后序遍历，预期输出结果：4,5,3,7,8,6,2,11,12,10,14,15,13,9,1
        afterOrderTraversalByStack(treeNode);
    }

    /**
     * 广度优先遍历测试
     *
     * @param treeNode
     */
    public static void testBreadthFirstTraversal(TreeNode treeNode) {
        //测试广度优先遍历,预期结果:1,2,9,3,6,10,13,4,5,7,8,11,12,14,15
        breadthFirstTraversalByQueue(treeNode);
    }


    public static TreeNode createTreeNode() {
        TreeNode node1 = new TreeNode();
        node1.setNodeData(1);
        TreeNode node2 = new TreeNode();
        node2.setNodeData(2);
        TreeNode node3 = new TreeNode();
        node3.setNodeData(3);
        TreeNode node4 = new TreeNode();
        node4.setNodeData(4);
        TreeNode node5 = new TreeNode();
        node5.setNodeData(5);
        TreeNode node6 = new TreeNode();
        node6.setNodeData(6);
        TreeNode node7 = new TreeNode();
        node7.setNodeData(7);
        TreeNode node8 = new TreeNode();
        node8.setNodeData(8);
        TreeNode node9 = new TreeNode();
        node9.setNodeData(9);
        TreeNode node10 = new TreeNode();
        node10.setNodeData(10);
        TreeNode node11 = new TreeNode();
        node11.setNodeData(11);
        TreeNode node12 = new TreeNode();
        node12.setNodeData(12);
        TreeNode node13 = new TreeNode();
        node13.setNodeData(13);
        TreeNode node14 = new TreeNode();
        node14.setNodeData(14);
        TreeNode node15 = new TreeNode();
        node15.setNodeData(15);

        node1.setLeftTreeNode(node2);
        node1.setRightTreeNode(node9);
        node2.setLeftTreeNode(node3);
        node2.setRightTreeNode(node6);
        node3.setLeftTreeNode(node4);
        node3.setRightTreeNode(node5);
        node6.setLeftTreeNode(node7);
        node6.setRightTreeNode(node8);
        node9.setLeftTreeNode(node10);
        node9.setRightTreeNode(node13);
        node10.setLeftTreeNode(node11);
        node10.setRightTreeNode(node12);
        node13.setLeftTreeNode(node14);
        node13.setRightTreeNode(node15);
        return node1;
    }

    /**
     * 深度优先遍历:前序遍历（递归）
     * 先打印树的根节点
     * 再打印树的左孩子节点
     * 最后打印树的右孩子节点
     *
     * @param treeNode
     */
    public static void preOrderTraversalByRecursive(TreeNode treeNode) {
        if (treeNode == null) {
            return;
        }
        //先打印当前节点的数据
        System.out.println(treeNode.getNodeData());
        //再打印当前节点的左节点的数据
        preOrderTraversalByRecursive(treeNode.getLeftTreeNode());
        //最后打印当前节点的右节点
        preOrderTraversalByRecursive(treeNode.getRightTreeNode());
    }

    /**
     * 深度优先遍历:前序遍历（栈）
     *
     * @param treeNode
     */
    public static void preOrderTraversalByStack(TreeNode treeNode) {
        Stack<TreeNode> stack = new Stack<>();
        Stack<TreeNode> mid = new Stack<>();
        TreeNode node = treeNode;
        while (node != null || !stack.isEmpty()) {
            //迭代访问节点的左孩子，并入栈
            while (node != null) {
                //打印根节点
                System.out.println(node.getNodeData());
                //将根节点入栈
                stack.push(node);
                //获取树的根节点的左节点
                node = node.getLeftTreeNode();
            }

            if (!stack.isEmpty()) {
                node = stack.pop();
                node = node.getRightTreeNode();
            }
        }
    }


    /**
     * 深度优先遍历:中序遍历
     * 先打印树的左孩子节点
     * 再打印树的根节点
     * 最后打印树的右孩子节点
     *
     * @param treeNode
     */
    public static void midOrderTraversal(TreeNode treeNode) {
        if (treeNode == null) {
            return;
        }
        //先打印左节点
        midOrderTraversal(treeNode.getLeftTreeNode());
        //再打印节点自身
        System.out.println(treeNode.getNodeData());
        //最后打印右节点
        midOrderTraversal(treeNode.getRightTreeNode());
    }

    /**
     * 中序遍历（stack）
     *
     * @param treeNode
     */
    public static void midOrderTraversalByStack(TreeNode treeNode) {
        Stack<TreeNode> stack = new Stack<>();
        TreeNode node = treeNode;
        while (node != null || !stack.isEmpty()) {
            while (node != null) {
                stack.push(node);
                node = node.getLeftTreeNode();
            }
            if (!stack.isEmpty()) {
                node = stack.pop();
                System.out.println(node.getNodeData());
                node = node.getRightTreeNode();
            }
        }
    }

    /**
     * 深度优先遍历:后序遍历
     * 先打印树的左孩子节点
     * 再打印树的右孩子节点
     * 最后打印树的根节点
     *
     * @param treeNode
     */
    public static void afterOrderTraversal(TreeNode treeNode) {
        if (treeNode == null) {
            return;
        }
        //先打印左节点
        afterOrderTraversal(treeNode.getLeftTreeNode());
        //再打印右节点
        afterOrderTraversal(treeNode.getRightTreeNode());
        //最后打印节点自身
        System.out.println(treeNode.getNodeData());
    }


    /**
     * 后序遍历（栈）
     * 如果当前弹栈的节点A，为栈里边的下一个节点B的左节点，表示左子树已经遍历完，当前节点为B节点的右孩子节点
     * 如果当前弹栈的节点为C，则表示右子树遍历完，当前节点应该为null,触发下一弹栈，弹出B节点
     *
     *==B
     *A   C
     * @param treeNode
     */
    public static void afterOrderTraversalByStack(TreeNode treeNode) {
        Stack<TreeNode> stack = new Stack<>();
        TreeNode node = treeNode;
        TreeNode temp = null;
        while (node != null || !stack.isEmpty()) {
            while (node != null) {
                stack.push(node);
                node = node.getLeftTreeNode();
            }
            while (!stack.isEmpty()) {
                 node = stack.pop();
                System.out.println(node.getNodeData());
                if(!stack.isEmpty()){
                    temp=stack.peek();
                }
                if(temp!=null&&temp.getLeftTreeNode()==node){
                    node=temp.getRightTreeNode();
                }else{
                    node=null;
                }
                temp=null;
            }
        }

    }

    /**
     * 广度优先遍历
     * @param treeNode
     */
    public static void breadthFirstTraversalByQueue(TreeNode treeNode) {
        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(treeNode);
        while (!queue.isEmpty()) {
            TreeNode node = queue.poll();
            System.out.println(node.getNodeData());
            if (node.getLeftTreeNode() != null) {
                queue.add(node.getLeftTreeNode());
            }
            if (node.getRightTreeNode() != null) {
                queue.add(node.getRightTreeNode());
            }
        }
    }

}

3、树基于栈的遍历（前，中，后遍历）

/**
     * 后序遍历
     *
     * @param node
     */
    public static void traverseAfterByStack(Node node) {

        Stack<Node> stack = new Stack<>();
        Node node1 = node;

        while (node1 != null || !stack.isEmpty()) {

            while (node1 != null) {
                stack.add(node1);
                node1 = node1.left;
            }

            Node node2 = stack.peek();
            //读出节点是父亲的左孩子节点
            if (node2.parent != null && node2.parent.left == node2) {
                System.out.println(node2.v);
                stack.pop();
                node1 = stack.peek() != null ? stack.peek().right : null;

            } else {
                System.out.println(node2.v);
                stack.pop();
                node1 = null;
            }

        }

    }


    /**
     * 中序遍历
     *
     * @param node
     */
    public static void traverseMindByStack(Node node) {
        Stack<Node> stack = new Stack<>();
        Node node1 = node;

        while (node1 != null || !stack.isEmpty()) {

            while (node1 != null) {
                stack.add(node1);
                node1 = node1.left;
            }


            Node node2 = stack.pop();
            System.out.println(node2.v);
            node1 = node2.right;
        }
    }


    /**
     * 前序遍历基于栈
     *
     * @param node
     */
    public static void traversBeforeByStack(Node node) {
        Stack<Node> stack = new Stack<>();

        Node node1 = node;
        //先打印前序节点,并将节点压入栈中。当节点的left孩子为空时,退出压栈动作
        while (node1 != null || !stack.isEmpty()) {

            //将节点压入栈中
            while (node1 != null) {
                System.out.println(node1.v);
                stack.push(node1);
                node1 = node1.left;
            }


            //从栈中读取数据
            Node node2 = stack.pop();
            node1 = node2.right;

        }

    }

4、二叉树的左视图 和 右视图

 /**
     * 构建一棵树
     *
     * @return
     */
    public static Node buildNode() {
        Node node = new Node("A");
        Node node1 = new Node("B");
        Node node2 = new Node("C");
        Node node3 = new Node("D");
        Node node4 = new Node("E");
        Node node5 = new Node("F");
        Node node6 = new Node("G");
        Node node7 = new Node("H");

        node.left = node1;
        node.right = node2;
        node1.parent = node;
        node2.parent = node;

        node1.left = node3;
        node1.right = node4;
        node3.parent = node1;
        node4.parent = node1;

        node2.left = node5;
        node2.right = node6;
        node5.parent = node2;
        node6.parent = node2;

        node3.left = node7;
        node7.parent = node3;

        return node;
    }


    /**
     * 二叉树的左视图：相等于层序遍历，每一层的第一个节点。
     * 基于两个队列，进行交换，来保存每一层树的节点，从而能读到每层的第一个节点，就是左视图的结果
     *
     * @param node
     * @return
     */
    public static List<String> leftView(Node node) {

        Queue<Node> nodeQueue1 = new LinkedList<>();
        Queue<Node> nodeQueue2 = new LinkedList<>();
        List<String> result = new ArrayList<>();

        nodeQueue1.add(node);
        boolean isFirst = true;
        while (nodeQueue1.size() != 0) {
            Node node1 = nodeQueue1.poll();

            if (isFirst) {
                result.add(node1.v);
                isFirst = false;
            }

            if (node1.left != null) {
                nodeQueue2.add(node1.left);
            }

            if (node1.right != null) {
                nodeQueue2.add(node1.right);
            }



            if (nodeQueue1.isEmpty()) {
                isFirst=true;
                Queue<Node> tmp = nodeQueue1;
                nodeQueue1 = nodeQueue2;
                nodeQueue2 = tmp;
            }
        }
        return result;

    }

    /**
     * 二叉树的右视图：相等于层序遍历，每一层的最后一个节点。
     * 基于两个队列，进行交换，来保存每一层树的节点，从而能读到每层的最后一个节点，就是右视图的结果
     *
     * @param node
     * @return
     */
    public static List<String> rightView(Node node) {

        Queue<Node> nodeQueue1 = new LinkedList<>();
        Queue<Node> nodeQueue2 = new LinkedList<>();
        List<String> result = new ArrayList<>();

        nodeQueue1.add(node);


        while (nodeQueue1.size() != 0) {
            Node node1 = nodeQueue1.poll();

            if (node1.left != null) {
                nodeQueue2.add(node1.left);
            }

            if (node1.right != null) {
                nodeQueue2.add(node1.right);
            }

            if (nodeQueue1.isEmpty()) {
                result.add(node1.v);
                Queue<Node> tmp = nodeQueue1;
                nodeQueue1 = nodeQueue2;
                nodeQueue2 = tmp;
            }
        }
        return result;

    }

5、二叉树的俯视图 和 仰视视图

/**
     * 树的仰视图
     * @param node
     * @return
     */
    public static void upView(Node node,List<String> result){
        if(node==null){
            return ;
        }
        if(node.left==null && node.right==null){
            result.add(node.v);
            return ;
        }
        upView(node.left,result);
        upView(node.right,result);
    }


    /**
     * 树的俯视图
     * @param node
     * @return
     */
    public static List<String> topView(Node node) {

        List<String> result = new ArrayList<>();

        if (node == null) {
            return result;
        }
        //添加根节点
        result.add(node.v);

        Node left = node.left;
        Node right = node.right;

        while (left != null || right != null) {

            if (left != null) {
                result.add(left.v);
                left = left.left;
            }

            if (right != null) {
                result.add(right.v);
                right = right.right;
            }
        }

        return result;

    }

 

二、二叉堆

1、二叉堆的向上调整，向下调整，构建二叉堆

package com.spring.test.service.algorithm.tree;

import java.util.Arrays;

/**
 * 二叉堆的公式：
 * 已知父节点下标,求子节点小标
 * leftChildIndex=parentIndex*2+1
 * rightChildIndex=parentIndex*2+2
 *
 * 已知子节点下标(不分左右),求父亲节点下标
 * parentIndex=(childIndex-1)/2
 *
 *
 * 本示例演练的为最小堆
 *
 * @author shangxiaofei
 * @date 8:09 PM 2019/6/2
 */
public class BinaryTreeHeap {

    /**
     * 节点上浮
     *
     * @param array      待调整的二叉堆
     * @param treeLength 二叉堆的大小
     */
    public static void upAdjust(int[] array, int treeLength) {
        //最后一个子节点的下标
        int childIndex = treeLength - 1;
        //计算它的父节点的下标
        int parentIndex = (childIndex - 1) / 2;
        //赋值需要上浮的节点的值
        int temp = array[childIndex];
        //开始上浮，孩子节点为0,代表已经到了堆顶
        while (childIndex > 0 && array[parentIndex] > temp) {
            //父节点和子节点进行交换
            array[childIndex] = array[parentIndex];
            //赋值新的孩子节点
            childIndex = parentIndex;
            //计算新的父节点
            parentIndex = (childIndex - 1) / 2;
        }
        //将上浮节点赋值给新的孩子节点
        array[childIndex] = temp;
    }

    /**
     * 节点下沉
     *
     * @param array       待调整的二叉堆
     * @param parentIndex 要下沉的父节点的下标
     * @param treeLength  二叉堆的大小
     */
    public static void downAdjust(int[] array, int parentIndex, int treeLength) {
        //先求出该父节点的左孩子节点的下标
        int childIndex = parentIndex * 2 + 1;
        //待调整的数
        int temp = array[parentIndex];
        //开始下沉,当孩子节点的下标小于树的长度时,表示还未到树的最后一个节点
        while (childIndex < treeLength) {
            if (childIndex + 1 < treeLength && array[childIndex] > array[childIndex + 1]) {
                //如果存在右孩子节点，且左孩子节点大于右孩子节点，则待下沉节点应该与右孩子节点进行比较
                childIndex++;
            }
            //如果待调整父节点,大于最小孩子节点,则进行位置替换
            if (temp > array[childIndex]) {
                array[parentIndex] = array[childIndex];
                //更新当前孩子节点为parentIndex
                parentIndex = childIndex;
                //计算最新的parentIndex节点的最新左孩子节点
                childIndex = parentIndex * 2 + 1;
                //继续比较孩子节点
                continue;
            }
            //下沉节点已经找到合适的位置，这个位置均小于左孩子和右孩子
            break;
        }
        array[parentIndex] = temp;
    }

    /**
     * 构建二叉堆
     *
     * @param array 要调整的普通数组，元素是满的
     */
    public static void bulidBinaryHeap(int[] array) {
        for (int i = (array.length - 2) / 2; i >= 0; i--) {
            downAdjust(array, i, array.length);
        }
    }


    public static void main(String[] args) {
        int[] heap = new int[]{7, 9, 4, 5, 8, 9, 10};
        //构建二叉堆
        bulidBinaryHeap(heap);
        System.out.println("待调整后的二叉堆为:" + Arrays.toString(heap));
        //待调整后的二叉堆为:[4, 5, 7, 9, 8, 9, 10]

        int[] heap1 = new int[]{4, 5, 7, 9, 8, 9, 10, 0};
        //向上调整
        upAdjust(heap1, heap1.length);
        System.out.println("向上调整后的堆为:" + Arrays.toString(heap1));
        //向上调整后的堆为:[0, 4, 7, 5, 8, 9, 10, 9]

        int[] heap2 = new int[]{10, 4, 5, 7, 9, 8};
        downAdjust(heap2, 0, heap2.length);
        System.out.println("向下调整后的堆为:" + Arrays.toString(heap2));
        //向下调整后的堆为:[4, 7, 5, 10, 9, 8]

    }
}

2、二叉堆数据结构

package com.sxf.study.interview.tree;

import java.util.PriorityQueue;

/**
 * @date 3:49 PM 2020/2/1
 */
public class BinaryHeapTest {

    /**
     * 二叉堆的公式
     * 已知父亲节点的下标，求子节点下标
     * leftIndex=2*parentIndex+1
     * rightIndex=2*parentIndex+2
     *
     * 已知孩子节点的下标，求父亲节点的下标
     * parentIndex=(childIndex-1)/2
     *
     * 加入一个节点：
     * 加入数组的最后一个元素，向上调整（已知孩子节点坐标，和父亲节点比较）
     *
     * 取出一个节点：
     * 取最顶节点，返回结果。将最尾部的元素放置在数组的头部，向下调整。（已知父亲节点坐标，和孩子元素进行对比）
     *
     * @param args
     */
    public static void main(String[] args) {

        PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();
        priorityQueue.add(1);
        priorityQueue.poll();

    }


}


/**
 * ==========1
 * ======2     3
 * ===4    5 6   7
 */
class BinaryHead {

    private Object[] node = new Object[10];

    private int nodeSize;

    /**
     * 添加一个节点
     *
     * @param data
     */
    public void push(String data) {
        //step1:元素为空，则抛出异常
        if (data == null) {
            throw new IllegalArgumentException("入参异常");
        }
        //step2:如果为第一个元素，则无需排序
        if (nodeSize == 0) {
            node[0] = data;
            nodeSize++;
            return;
        }
        //判断元素的个数>=数组的长度，则需要扩容（本示例不扩容，忽略默认数组长度够用）

        //step3:开始向上调整
        //当前数组最后一个空的下标位置
        int childIndex = nodeSize;
        nodeSize++;
        siftUp(childIndex,data);
    }

    /**
     * 向上调整
     * @param index
     * @param data
     */
    private void siftUp(int index, Object data) {
        Comparable dataComparable = (Comparable) data;
        //获取该位置的孩子节点的父亲节点的位置
        while (index > 0) {
            int parentIndex = (index - 1) / 2;
            Comparable parentData = (Comparable) node[parentIndex];
            //孩子节点大于等于父亲节点，则无需进行调整
            if (dataComparable.compareTo(parentData) >= 0) {
                break;
            }
            //孩子节点的数据小于父亲节点=>父亲节点和孩子节点进行位置替换,
            node[index]=parentData;
            index=parentIndex;
        }
        node[index] = dataComparable;
    }


    /**
     * 弹出1个节点
     *
     * @return
     */
    public String poll() {
        //step1:当个数为0,返回null
        if(nodeSize==0){
            return null;
        }
        //step2:取出最小的元素
        String result= (String) node[0];
        //step3:元素个数减少1个,并得到最后一个元素，将最后一个元素的位置设置为null
        nodeSize--;
        int lastNodeIndex=nodeSize;
        Object lastNode=node[lastNodeIndex];
        node[lastNodeIndex]=null;
        //step4:向下调整
        siftDown(0,lastNode);
        return result;
    }

    /**
     * 向下调整
     * @param index
     * @param data
     */
    private void siftDown(int index,Object data){
        Comparable dataComparable= (Comparable) data;
        //获取最后1个没有孩子下标的元素，最后比较的临界值
        int lastParentIndex=nodeSize/2;
        while (index<lastParentIndex){
            //左孩子节点的位置
            int leftChildIndex=index*2+1;
            //右孩子节点的位置
            int rightChildIndex=leftChildIndex+1;

            //待调整元素和其两个孩子中最小的元素进行比较（最起码有左孩子，但不一定有右孩子）
            int comparableChildIndex=leftChildIndex;
            Comparable comparableChildData= (Comparable) node[leftChildIndex];

            //如果存在右孩子，则在两个孩子中找到最小的那个元素进行比较
            if(rightChildIndex<nodeSize&&comparableChildData.compareTo(node[rightChildIndex])>0){
                //左孩子大于右孩子，则和右孩子进行比较
                comparableChildIndex=rightChildIndex;
                comparableChildData= (Comparable) node[comparableChildIndex];
            }

            if(dataComparable.compareTo(comparableChildData)<=0){
                //如果待调整元素小于其孩子节点
                break;
            }

            //将小的元素上浮
            node[index]=comparableChildData;
            //待比较的位置下沉
            index=comparableChildIndex;
        }
        node[index]=dataComparable;
    }
}

3、将一个数组（数组的每一个下标都存在数据）调整为二叉堆

/**
     * 构建最小堆
     * 将一个普通数组构建成二叉堆
     * 法则：从一个数组中的最后一个父亲节点开始，对每一个父亲节点一次做下沉操作，调整到数组的头节点
     * @param objects
     */
    public static void buildBinaryHeap(Object[] objects){
        int length=objects.length;
        int lastIndex=length-1;
        //最后一个父亲节点
        int lastParentIndex=(lastIndex-1)/2;
        //从最后1个父亲节点依次向下调整，直到调整至数组的头节点，调整完毕，二叉堆就形成了
        for(int i=lastIndex;i>=0;i--){
            siftDownArray(objects,i,length);
        }
    }

    public static void siftDownArray(Object[] objects,int lastParentIndex,int dataSize){
        //要调整的数据
        Comparable comparableData= (Comparable) objects[lastParentIndex];
        //要调整的元素下标小于数组长度
        while (lastParentIndex<dataSize){
            int childIndex=lastParentIndex*2+1;
            Comparable comparableChildData= (Comparable) objects[childIndex];
            int rightChildIndex=childIndex+1;
            if(rightChildIndex<dataSize && comparableChildData.compareTo(objects[rightChildIndex])>0){
                //左右孩子节点比较，找出最小的的子节点
                childIndex=rightChildIndex;
                comparableChildData= (Comparable) objects[childIndex];
            }

            //如果比较的节点小于或等于孩子节点，则终止调整
            if(comparableData.compareTo(comparableChildData)<=0){
                break;
            }
            objects[lastParentIndex]=comparableChildData;
            lastParentIndex=childIndex;
        }
        objects[lastParentIndex]=comparableData;
    }