【数据结构和算法】归并排序

转载来自：https://blog.csdn.net/qq_36442947/article/details/81612870

1、原理

归并排序是一种概念上最简单的排序算法，与快速排序一样，归并排序也是基于分治法的。归并排序将待排序的元素序列分成两个长度相等的子序列，为每一个子序列排序，然后再将他们合并成一个子序列。合并两个子序列的过程也就是两路归并。

2、复杂度

归并排序是一种稳定的排序算法，归并排序的主要问题在于它需要一个与待排序数组一样大的辅助数组空间。由于归并排序每次划分时两个子序列的长度基本一样，所以归并排序最好、最差和平均时间复杂度都是n*lgn。
我们可以通过下图非常容易看懂归并排序的过程：
要将两个排好序的子序列合并为一个子序列的方法：每次都是从未比较的两个子序列的最小值中选出一个更小值。

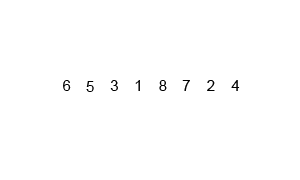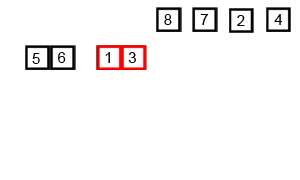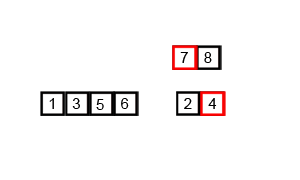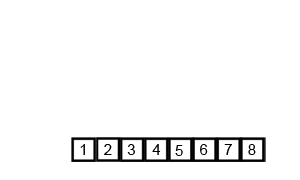
3、java代码

package com.spring.test.service.algorithm.sort;

/**
 * @author
 * 归并排序算法
 * @date 5:15 PM 2019/5/19
 */
public class MergerSort {


    public static void main(String[] args) {
        int[] array = {9, 0, 5, 6, 8, 7, 1, 4, 3, 2};
        mergeSort(array);

        for (int a : array) {
            System.out.println(a);
        }
    }


    /**
     * 归并排序
     *
     * @param array
     * @return
     */
    public static int[] mergeSort(int[] array) {
        mergeSort(array, 0, array.length - 1);
        return array;
    }


    private static void mergeSort(int[] array, int start, int end) {
        //如果起始坐标不小于结束坐标，说明当前数组只有一个元素，不用进行排序
        if (start < end) {
            //将数组进行拆分，分成左数组，右数组
            int mid = (start + end) / 2;
            //递归调用自身，对左数组进行排序
            mergeSort(array, start, mid);
            //递归调用自身，对右数组进行排序
            mergeSort(array, mid + 1, end);
            //将左右数组进行合并排序
            merge(array, start, mid, end);
        }

    }


    private static void merge(int[] array, int left, int mid, int right) {
        //声明临时数组，用于存放左右数组最终完成排序的数据
        int[] temp = new int[(right - left + 1)];
        //初始化左右数据的开始下标
        int l = left;
        int r = mid + 1;
        int k = 0;
        //每次从左右数组中拿出最小数据，进行对比，小的放入临时数组
        while (l <= mid && r <= right) {
            if (array[l] <= array[r]) {
                temp[k++] = array[l++];
            } else {
                temp[k++] = array[r++];
            }
        }
        //如果左侧数组未比较完，则将剩余的元素copy至临时数据
        while (l <= mid) {
            temp[k++] = array[l++];
        }
        //如果右侧数组未比较完，则将剩余的元素copy至临时数据
        while (r <= right) {
            temp[k++] = array[r++];
        }
        //复制回原数组
        for (int e : temp) {
            array[left++] = e;
        }
    }


}

 

案例二

public static int[] mergeSort(int[] array) {
        if (array == null || array.length <= 1) {
            return array;
        }
        return mergeSort(array, 0, array.length - 1);
    }


    private static int[] mergeSort(int[] array, int leftIndex, int rightIndex) {
        //如果左边元素下标等于右边数组下标，则认为是1个元素，无需进行排序
        if (leftIndex == rightIndex) {
            return new int[]{array[rightIndex]};
        }
        //求出元素下标的中间值
        int mindIdex = (leftIndex + rightIndex) / 2;
        //递归对左边元素进行排序
        int[] leftArray = mergeSort(array, leftIndex, mindIdex);
        //递归对右边元素进行排序
        int[] rightArray = mergeSort(array, mindIdex + 1, rightIndex);
        //将左右两个有序的数组进行合并
        return merge(leftArray, rightArray);
    }


    private static int[] merge(int[] leftArray, int[] rightArray) {
        int[] result = new int[leftArray.length + rightArray.length];
        int leftScanIndex = 0;
        int rightScanIndex = 0;
        int leftLength = leftArray.length;
        int rightLength = rightArray.length;
        int resultIndex = 0;

        // 如果两个数组都扫描完则中断循环
        while (leftScanIndex<leftLength || rightScanIndex<rightLength) {

            //左边数组的元素 和 右边数组的元素 进行比较
            while ((leftScanIndex < leftLength) && (rightScanIndex < rightLength) && leftArray[leftScanIndex] <= rightArray[rightScanIndex]) {
                result[resultIndex++] = leftArray[leftScanIndex++];
            }

            //右边数组的元素 和 左边数组的元素 进行比较
            while ((rightScanIndex < rightLength) && (leftScanIndex < leftLength) && rightArray[rightScanIndex] < leftArray[leftScanIndex]) {
                result[resultIndex++] = rightArray[rightScanIndex++];
            }

            //如果左边数组已经扫描完,右边数组没有扫描完,则将右边剩余元素添加到数组中
            if(leftScanIndex>=leftLength && rightScanIndex<rightLength){
                for(;rightScanIndex<rightLength;rightScanIndex++){
                    result[resultIndex++] = rightArray[rightScanIndex];
                }
            }

            //如果右边数组已经扫描完，左边数组还没有扫描完，则将左边剩余元素添加到数组中
            if(rightScanIndex>=rightLength && leftScanIndex<leftLength){
                for(;leftScanIndex<leftLength;leftScanIndex++){
                    result[resultIndex++]=leftArray[leftScanIndex];
                }
            }
        }

        return result;
    }