iris 数据集训练一个核 SVM 模型，可视化其决策区域

1、定义分类模型决策区域可视化的函数

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap

def plot_decision_regions(X, y, classifier, test_idx=None, resolution=0.02):
    
    # 定义颜色和标记符号，通过颜色列图表生成颜色示例图
    marker = ('o', 'x', 's', 'v', '^')
    colors = ('lightgreen', 'blue', 'red', 'cyan', 'gray')
    cmap = ListedColormap(colors[:len(np.unique(y))])

    # 可视化决策边界
    x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
                           np.arange(x2_min, x2_max, resolution))
    Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
    Z = Z.reshape(xx1.shape)
    
    plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)
    plt.xlim(xx1.min(), xx1.max())
    plt.ylim(xx2.min(), xx2.max())
    
    # 绘制所有的样本点
    for idx, cl in enumerate(np.unique(y)):
        plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1], alpha=0.8,
                    c=cmap(idx), marker=marker[idx], s=73, label=cl)
    
    # 使用小圆圈高亮显示测试集的样本
    if test_idx:
        X_test, y_test = X[test_idx, :], y[test_idx]
        plt.scatter(X_test[:, 0], X_test[:, 1], c='', alpha=1.0, linewidth=1,
                    edgecolors='black', marker='o', s=135, label='test set')

2、准备数据

from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

iris = datasets.load_iris()
X = iris.data[:, [2, 3]]
y = iris.target

# 划分测试集和训练集
X_train, X_test, y_train, y_test = train_test_split( 
            X, y, test_size=0.3, random_state=0)

# 对特征值进行标准化
sc = StandardScaler()
sc.fit(X_train)
X_train_std = sc.transform(X_train)
X_test_std = sc.transform(X_test)

# 将标准化后的训练数据和测试数据重新整合到一起
X_combined_std = np.vstack((X_train_std, X_test_std))
y_combined = np.hstack((y_train, y_test))

3、训练模型、绘制图形

from sklearn.svm import SVC
import matplotlib.pyplot as plt

%matplotlib inline
plt.rcParams['font.sans-serif'] = 'SimHei'
plt.rcParams['axes.unicode_minus'] = False

svm = SVC(kernel='rbf', random_state=0, gamma=0.10, C=10.0)
svm.fit(X_train_std, y_train)

plt.figure(figsize=(12, 7))
plot_decision_regions(X_combined_std, y_combined, classifier=svm,
                      test_idx=range(105, 150))
plt.title('核 SVM 模型的决策区域', fontsize=19, color='w')
plt.xlabel('标准化处理后的花瓣长度', fontsize=15)
plt.ylabel('标准化处理后的花瓣宽度', fontsize=15)
plt.legend(loc=2, scatterpoints=2)

图形如下：

 

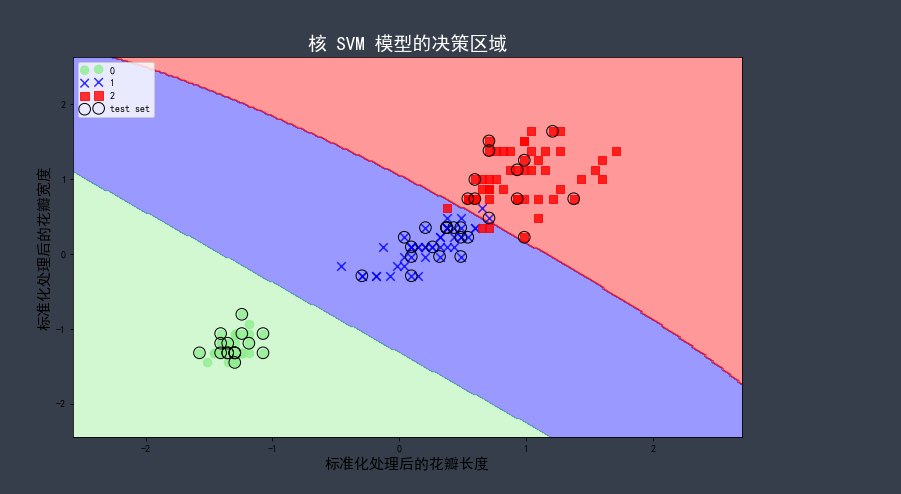
 如图所示，γ=0.10 相对角小，决策边界较为宽松。

增大 γ 值：

from sklearn.svm import SVC
import matplotlib.pyplot as plt

%matplotlib inline
plt.rcParams['font.sans-serif'] = 'SimHei'
plt.rcParams['axes.unicode_minus'] = False

svm = SVC(kernel='rbf', random_state=0, gamma=10, C=10.0)
svm.fit(X_train_std, y_train)

plt.figure(figsize=(12, 7))
plot_decision_regions(X_combined_std, y_combined, classifier=svm,
                      test_idx=range(105, 150))
plt.title('核 SVM 模型的决策区域', fontsize=19, color='w')
plt.xlabel('标准化处理后的花瓣长度', fontsize=15)
plt.ylabel('标准化处理后的花瓣宽度', fontsize=15)
plt.legend(loc=2, scatterpoints=2)

 图形如下：

 

 如图所示，类别 0 和 1 的决策边界随 γ 值的增大紧凑了许多。此模型虽然随训练数据拟合的很好，但对未知数据会有较高的泛化误差。