精度与分辨率是一回事吗
编码器精度与分辨率的区别
光看分辨率不行的,如果分辨出的位数似乎很多但都不准,那这样的分辨率意义不大。
前些年有人用两片8位AD拼成16位AD,表面上分辨率提高了一倍,但精度并未增加,
如果这么简单就达到精度的提高,那AD公司光用AD0808就行了也就不必花大力气研发16位以至更高位AD了
分辨率就是你能看出A和B身高差多少,精度就是A和B身高分别是多少。
分辨率是对数据的测量的精细程度,精度是准不准。
比如你用数字游标卡尺量一个10厘米的模型,显示结果为 50.1276厘米。
可以看出分辨率挺高,精度不咋地。
分辨率简单的说就是小数点后面的位数,比如4.201V的分辨率比4.20V高 但是分辨率高不代表精度高
如果这个电压本来是4.203V,高分辨率测出来是4.223V,低分辨率测出来是4.20V,那么低分辨率的精度高
“分辨率”和“精确度”——即Resolution和Accuracy。
ADC分辨率由数字化输入信号时所使用的比特数决定。
而精确度是指对于给定模拟输入,实际数字输出与理论预期数字输出之间的接近度。
换而言之,转换器的精确度决定了数字输出代码中有多少个比特表示有关输入信号的有用信息。
分辨力也称为分辨率,是指指示装置有效地辨别紧密相邻值的能力。
一般认为数字装置的分辨力就是最后一位数字,模拟装置分辨力为指示标尺分度值的一半。
测量精度是泛指测量结果的可信度,但不是规范用语。
用2.000V量程的三位半数字电压表举例来说,它的分辨力是0.001V,假设其精度是0.8%±3个字。
假如现在有三个个电压的真实值是x=1.6780V,y=1.6785V,z=1.6790V。
分辨力就是,它能判别出电压x与z之间相差0.001V,即测量z显示的数字肯定比x大0.001;
但是它无法判别x与y之间和y与z之间的区别,即测量y时可能显示的与x一样,也可能显示的与z一样,是不确定的。
精度大概的意思就是测量值与真实值之间的最大差距。
比如,这个表测量x电压,它可能显示的是1.688,也可能显示的是1.665,
也可能是别的什么数,但是范围不超过2.000x0.8%±3个字=±0.019V。
也就是说这个表测量x电压时显示1.659V-1.697V之间都算没问题。
简单点,做一个电压表,10位AD测10V电压,基本上每一格就是
10V/2^10=10/1024=0.01V,这是分辨率,表示它的分辨能力是每格就是0.01V,
但是由于积分电容不好,电阻温飘大,外部干扰,AD本身非线性等,
一个真正精确的10V电压你测出来是9.51V(分辨率决定了你最后一位小数的位置--十分位,还是百分位等),
这时你的分辨率是够高了,0.01V分辨率啊,但精度呢?差了0.5/10V=5%!
总之,分辨率可以上得很高,大不了增加AD位数,
你分辨率小数点后位数再多,但受其它因素影响,但精度却不能提高。
分辨率通常理解为A/D转换精度或能感知的最小变化而精度通常指:
分辨率就是传感器的灵敏度,即引起输出变化的最小输入量,
国产温度传感器的精度分A、B两个级别,国标规定如下:
精度——是指在真值附近正负三倍标准差的值与量程之比,是指测量值与真值的最大差异;
关于精密度Precision 准确度Accuracy 和 分辨率Resolution
一把塑料尺子,最小刻度是1mm,拿它量东西,就不能读出1mm以下的数来,
那么这个1mm就是它的(最小)分辨率,即最小可分辨的度量。
如果已经知道一个物体的实际长度是100mm,拿这把尺子来测量,量出来的数据是102mm,
那么这个尺子的准确度就是(102-100)/100=0.02,即测量结果与真实数值之间的误差。
再说一个概念精密度Precision,这个是指同一个仪器每次测量数值之间的离散程度,比较的对象是自己每次测量的数据。
也用上文的尺子做测量,还是上次的那一个物体,测了5次,数据分别是108,109,107,107,108,108。
这些数据和真实值100mm之间的误差都不小,但是这些数据之间的差距都很小,说明精密度不错。
精密度Precision + 准确度Accuracy = 精确度。
很多人常常把 精密度Precision 误判断为精度,
也有些仪器厂家误导使用者故意使用精密度代替精度。一般而言大家讲的精度都是指准确度。
分辨率与精度的关系能够用下面的几个图证明:
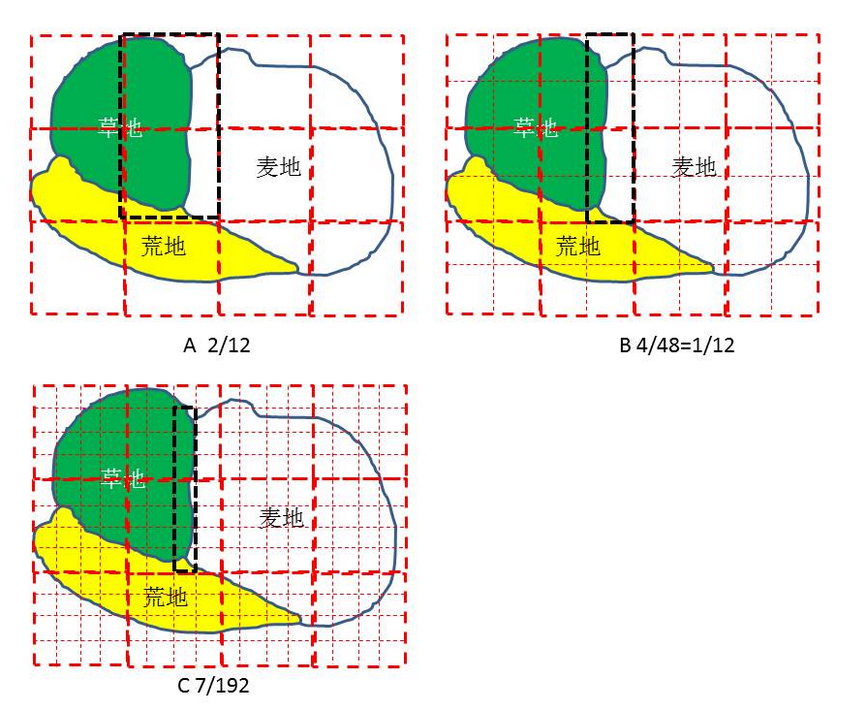

上面四个图是相同的面积,让我们看草地与麦地的边界(请注意黑框中的边界格子)。
图A有12格子,边界格子是2格,如此这两个格子是不确定的,因此,不确定度是2/12。
同理,图B中有48个格子,有四个边界格子,如此, 不确定度是4/48。
图C 不确定度是7/192. 图D是不确定度是12/768。
不确定度降低,自然精度就提高,证毕
关于A/D的精度、分辨率与LSB误差的大扫盲
我们所讲的精度通常是指它的精确度,其实这是错误的。
精度又叫做精密度,是跟准确度相对应的一个概念。
就像打靶一样,打的准,那就说它的准确度比较高;
而每两个靶之间能打出的偏移越小,那它的精密度就越高。
精密度 + 准确度 = 精确度。
但是鉴于大家都将精度指代了精确度,那以下所说的精度如无特别指出,都是指精确度。
很多人对于精度和分辨率的概念不清楚,这里我做一下总结,希望大家不要混淆。
我们搞电子开发的,经常跟“精度”与“分辨率”打交道,这个问题不是三言两语能搞得清楚的,在这里只作抛砖引玉了。
简单点说,“精度”是用来描述物理量的准确程度的,而“分辨率”是用来描述刻度划分的。
从定义上看,这两个量应该是风马牛不相及的。(是不是有朋友感到愕然^_^)。
很多卖传感器的JS就是利用这一点来糊弄人的了。简单做个比喻:
有这么一把常见的塑料尺(中学生用的那种),它的量程是10厘米,上面有100个刻度,最小能读出1毫米的有效值。
那么我们就说这把尺子的分辨率是1毫米,或者量程的1%;
而它的实际精度就不得而知了(算是0.1毫米吧)。
当我们用火来烤一下它,并且把它拉长一段,然后再考察一下它。
我们不难发现,它还有有100个刻度,它的“分辨率”还是1毫米,跟原来一样!
然而,您还会认为它的精度还是原来的0.1毫米么?(这个例子是引用网上的,个人觉得比喻的很形象!)
回到电子技术上,我们考察一个常用的数字温度传感器:AD7416。
供应商只是大肆宣扬它有10位的AD,分辨率是1/1024。
那么,很多人就会这么欣喜:哇塞,如果测量温度0-100摄氏度,100/1024……约等于0.098摄氏度!
这么高的精度,足够用了。但是我们去浏览一下AD7416的数据手册,居然发现里面赫然写着:测量精度0.25摄氏度!
所以说分辨率跟精度完全是两回事,在这个温度传感器里,只要你愿意,你甚至可以用一个14位的AD,获得1/16384的分辨率,但是测量值的精度还是0.25摄氏度^_^
所以很多朋友一谈到精度,马上就和分辨率联系起来了,包括有些项目负责人,只会在那里说:这个系统精度要求很高啊,你们AD的位数至少要多少多少啊……
其实,仔细浏览一下AD的数据手册,会发现跟精度有关的有两个很重要的指标:
DNL和INL。似乎知道这两个指标的朋友并不多,所以在这里很有必要解释一下。
DNL:Differencial NonLiner——微分非线性度
INL:Interger NonLiner——积分非线性度(精度主要用这个值来表示)
他表示了ADC器件在所有的数值点上对应的模拟值,和真实值之间误差最大的那一点的误差值。
也就是,输出数值偏离线性最大的距离。单位是LSB(即最低位所表示的量)。
当然,像有的AD如△—∑系列的AD,也用Linearity error 来表示精度。
为什么有的AD很贵,就是因为INL很低。
分辨率同为12bit的两个ADC,一个INL=±3LSB,而一个做到了±1.5LSB,那么他们的价格可能相差一倍。
LSB(Least Significant Bit),意为最低有效位;
MSB(Most Significant Bit),意为最高有效位,
若MSB=1,则表示数据为负值,若MSB=0,则表示数据为正。
当选择模数转换器(ADC)时,最低有效位(LSB)这一参数的含义是什么?
有位工程师告诉我某某生产商的某款12位转换器只有7个可用位。
也就是说,所谓12位的转换器实际上只有7位。他的结论是根据器件的失调误差和增益误差参数得出的,
这两个参数的最大值如下:
失调误差 =±3LSB,
增益误差 =±5LSB,
乍一看,觉得他似乎是对的。从上面列出的参数可知最差的技术参数是增益误差(±5 LSB)。
进行简单的数学运算,12位减去5位分辨率等于7位,对吗?
果真如此的话,ADC生产商为何还要推出这样的器件呢?
增益误差参数似乎表明只要购买成本更低的8位转换器就可以了,但看起来这又有点不对劲了。
正如您所判断的,上面的说法是错误的。
让我们重新来看一下LSB的定义。考虑一个12位串行转换器,它会输出由1或0组成的12位数串。
通常,转换器首先送出的是最高有效位(MSB)(即LSB + 11)。有些转换器也会先送出LSB。
在下面的讨论中,我们假设先送出的是MSB(如图1所示),
然后依次送出MSB-1 (即 LSB + 10)和MSB -2(即LSB + 9)并依次类推。
转换器最终送出MSB -11(即LSB)作为位串的末位。
LSB这一术语有着特定的含义,它表示的是数字流中的最后一位,也表示组成满量程输入范围的最小单位。
对于12位转换器来说,LSB的值相当于模拟信号满量程输入范围除以2^12 或 4,096的商。
如果用真实的数字来表示的话,对于满量程输入范围为4.096V的情况,一个12位转换器对应的LSB大小为1mV。
但是,将LSB定义为4096个可能编码中的一个编码对于我们的理解是有好处的。
让我们回到开头的技术指标,并将其转换到满量程输入范围为4.096V的12位转换器中:
失调误差 = ±3LSB =±3mV,
增益误差 =±5LSB = ±5mV,
这些技术参数表明转换器转换过程引入的误差最大仅为8mV(或 8个编码)。
这绝不是说误差发生在转换器输出位流的LSB、LSB-1、LSB-2、LSB-3、LSB-4、LSB-5、LSB-6和 LSB-7 八个位上,而是表示误差最大是一个LSB的八倍(或8mV)。
准确地说,转换器的传递函数可能造成在4,096个编码中丢失最多8个编码。
丢失的只可能是最低端或最高端的编码。
例如,误差为+8LSB ((+3LSB失调误差) + (+5LSB增益误差)) 的一个12位转换器可能输出的编码范围为0 至 4,088。
丢失的编码为4088至4095。相对于满量程这一误差很小仅为其0.2%。
与此相对,一个误差为-3LSB((-3LSB失调误差)—(-5LSB增益误差))的12位转换器输出的编码范围为3至4,095。此时增益误差会造成精度下降,但不会使编码丢失。丢
失的编码为0、1和2。这两个例子给出的都是最坏情况。在实际的转换器中,失调误差和增益误差很少会如此接近最大值。
在实际应用中,由于ADC失调或增益参数的改进而使性能提升的程度微不足道,甚至可以忽略。
但是,对于那些将精度作为一项设计目标的设计人员来说,这种假设太过绝对。
利用固件设计可以很容易地实现数字校准算法。但更重要的是,电路的前端放大/信号调理部分通常会产生比转换器本身更大的误差。
通过上面的讨论可以对本文开头提到的错误结论有一个更为全面而清晰的认识。
事实上,上述的12位转换器的精度约为11.997位。采用微处理器或单片机可以利用简单的校准算法消除这种失调和增益误差,这对设计人员来说无疑是个好消息。
本文来自CSDN博客,转载请标明出处:http://blog.csdn.net/jhjGeneral/archive/2009/03/24/4019447.aspx
分辨率和精度之间的差异。
在与使用模数转换器 (ADC) 的系统设计人员进行交谈时,我最常听到的一个问题就是:
“你的16位ADC的精度也是16位的吗?”
这个问题的答案取决于对分辨率和精度概念的基本理解。尽管是两个完全不同的概念,这两个数据项经常被搞混和交换使用。
今天的博文详述了这两个概念间的差异。我们将在一系列帖子中深入研究造成ADC不准确的主要原因。
ADC的分辨率被定义为输入信号值的最小变化,这个最小数值变化会改变数字输出值的一个数值。
对于一个理想ADC来说,传递函数是一个步宽等于分辨率的阶梯。
然而,在具有较高分辨率的系统中(≥16位),传输函数的响应将相对于理想响应有一个较大的偏离。
这是因为ADC以及驱动器电路导致的噪声会降低ADC的分辨率。
此外,如果DC电压被施加到理想ADC的输入上并且执行多个转换的话,数字输出应该始终为同样的代码(由图1中的黑点表示)。
现实中,根据总体系统噪声(也就是包括电压基准和驱动器电路),输出代码被分布在多个代码上(由下面的一团红点表示)。
系统中的噪声越多,数据点的集合就越宽,反之亦然。
图1中显示的是一个中量程DC输入的示例。ADC传递函数上输出点的集合通常被表现为ADC数据表中的DC柱状图。
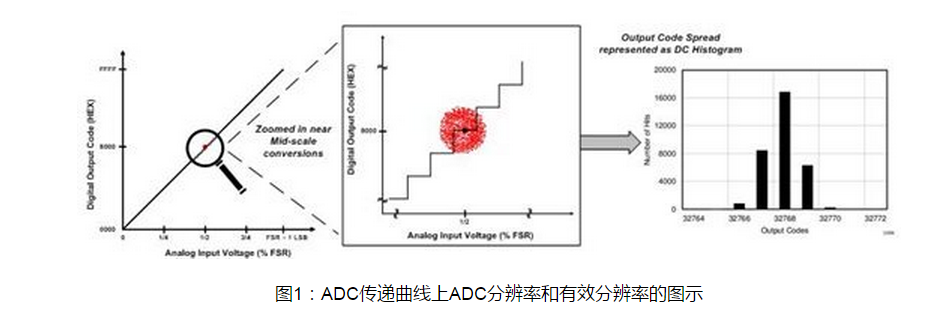
图1中的图表提出了一个有意思的问题。
如果同样的模拟输入会导致多个数字输出,那么对于ADC分辨率的定义仍然有效吗?
是的,前提是我们只考虑ADC的量化噪声。
然而,当我们将信号链中所有的噪声和失真计算在内时,
正如等式 (1) 中所显示的那样,ADC的有效无噪声分辨率取决于输出代码分布 (NPP)。
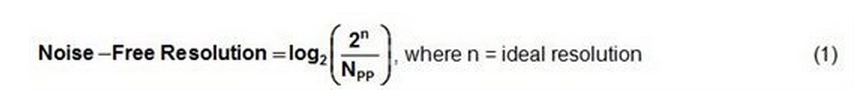
在典型ADC数据表中,有效位数 (ENOB) 间接地由AC参数和信噪失真比 (SINAD) 指定,可使用方程式2计算得出:
下面,考虑一下图1中的输出代码簇(红点)不是位于理想输出代码的中央,
而是位于远离黑点的ADC传递曲线上的其他位置(如图2中所示)。
这个距离是指示出采集系统精度。
不但ADC,还有前端驱动电路、基准和基准缓冲器都会影响到总体系统精度。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号