漫谈递归
https://zh.wikipedia.org/wiki/%E9%80%92%E5%BD%92
递归(英语:Recursion),又译为递回,在数学与计算机科学中,是指在函数的定义中使用函数自身的方法。
递归一词还较常用于描述以自相似方法重复事物的过程。例如,当两面镜子相互之间近似平行时,镜中嵌套的图像是以无限递归的形式出现的。
语言例子
从前有座山,山里有座庙,庙里有个老和尚,正在给小和尚讲故事呢!故事是什么呢?
“从前有座山,山里有座庙,庙里有个老和尚,正在给小和尚讲故事呢!故事是什么呢?
‘从前有座山,山里有座庙,庙里有个老和尚,正在给小和尚讲故事呢!故事是什么呢?……’”
以下是另一个可能更有利于理解递归过程的解释:
我们已经完成了吗?如果完成了,返回结果。如果没有这样的终止条件,递归将会永远地继续下去。
如果没有,则简化问题,解决较容易的问题,并将结果组装成原始问题的解决办法。然后返回该解决办法。
这样就有一种更有趣的描述:“为了理解递归,则必须首先理解递归。”或者更准确地,按照安德鲁·普洛特金的解释:
“如果你已经知道了什么是递归,只需记住答案。否则,找一个比你更接近侯世达的人;然后让他/她来告诉你什么是递归。”
https://zh.wikipedia.org/wiki/%E4%BE%AF%E4%B8%96%E8%BE%BE%E5%AE%9A%E5%BE%8B
侯世达定律(英语:Hofstadter's law)是一句自指的格言,由侯世达在《哥德尔、埃舍尔、巴赫》一书中提出:
侯世达定律:做事所花费的时间总是比你预期的要长,即使你的预期中考虑了侯世达定律。——侯世达,于《哥德尔、埃舍尔、巴赫》
侯世达定律指做复杂任务需要花费的时间总是很难预计的。
程序员经常会引用这一定律,特别是在进行有关提高效率的讨论时(如《人月神话》和极限编程)。
其自指的特征反映了即便意识到任务的复杂性,预计花费的时间仍是困难的。
这一定律最初是描述早年国际象棋人机对弈的现象。
侯世达写道:“计算机下国际象棋的早期阶段,有人曾估计再要十年的时间计算机(或程序)就能得到世界冠军。
可是,十年过去之后,计算机要成为世界冠军似乎还要再过十年……”
他将这一现象看作是递归化的侯世达定律的一个例证。
http://www.nowamagic.net/librarys/veda/detail/2314
为什么要用递归
编程里面估计最让人摸不着头脑的基本算法就是递归了。很多时候我们看明白一个复杂的递归都有点费时间,尤其对模型所描述的问题概念不清的时候,想要自己设计一个递归那么就更是有难度了。
很多不理解递归的人(今天在csdn里面看到一个初学者的留言),总认为递归完全没必要,用循环就可以实现,其实这是一种很肤浅的理解。因为递归之所以在程序中能风靡并不是因为他的循环,大家都知道递归分两步,递和归,那么可以知道递归对于空间性能来说,简直就是造孽,这对于追求时空完美的人来说,简直无法接接受,如果递归仅仅是循环,估计现在我们就看不到递归了。递归之所以现在还存在是因为递归可以产生无限循环体,也就是说有可能产生100层也可能10000层for循环。例如对于一个字符串进行全排列,字符串长度不定,那么如果你用循环来实现,你会发现你根本写不出来,这个时候就要调用递归,而且在递归模型里面还可以使用分支递归,例如for循环与递归嵌套,或者这节枚举几个递归步进表达式,每一个形成一个递归。
用归纳法来理解递归
数学都不差的我们,第一反应就是递归在数学上的模型是什么。毕竟我们对于问题进行数学建模比起代码建模拿手多了。 (当然如果对于问题很清楚的人也可以直接简历递归模型了,运用数模做中介的是针对对于那些问题还不是很清楚的人)
自己观察递归,我们会发现,递归的数学模型其实就是归纳法,这个在高中的数列里面是最常用的了。回忆一下归纳法。
归纳法适用于想解决一个问题转化为解决他的子问题,而他的子问题又变成子问题的子问题,而且我们发现这些问题其实都是一个模型,也就是说存在相同的逻辑归纳处理项。当然有一个是例外的,也就是递归结束的哪一个处理方法不适用于我们的归纳处理项,当然也不能适用,否则我们就无穷递归了。这里又引出了一个归纳终结点以及直接求解的表达式。如果运用列表来形容归纳法就是:
- 步进表达式:问题蜕变成子问题的表达式
- 结束条件:什么时候可以不再是用步进表达式
- 直接求解表达式:在结束条件下能够直接计算返回值的表达式
- 逻辑归纳项:适用于一切非适用于结束条件的子问题的处理,当然上面的步进表达式其实就是包含在这里面了。
这样其实就结束了,递归也就出来了。递归算法的一般形式:
void func( mode ) { if ( endCondition ) { constExpression //基本项 } else { accumrateExpreesion //归纳项 mode = expression //步进表达式 func (mode) //调用本身,递归 } }
最典型的就是N!算法,这个最具有说服力。理解了递归的思想以及使用场景,基本就能自己设计了,当然要想和其他算法结合起来使用,还需要不断实践与总结了。
#include "stdio.h" #include "math.h" int main( void ) { int n, rs; printf( "请输入需要计算阶乘的数n:" ); scanf( "%d", &n ); rs = factorial( n ); printf( "%d ", rs ); } // 递归计算过程 int factorial( n ) { if ( n == 1 ) { return 1; } return n * factorial( n - 1 ); }
返回一个二叉树的深度:
int depth( Tree t ) { if ( !t ) return 0; else { int a = depth( t.right ); int b = depth( t.left ); return ( a > b ) ? ( a + 1 ) : ( b + 1 ); } }
算法的思想是:如果这个树是空,则返回0;否则先求左边树的深度,再求右边数的深度,然后对这两个值进行比较哪个大就取哪个值+1。
判断一个二叉树是否平衡:
int isB( Tree t ) { if ( !t ) return 0; int left = isB( t.left ); int right = isB( t.right ); if ( left >= 0 && right >= 0 && left - right <= 1 || left - right >= -1 ) return ( left < right ) ? ( right + 1 ) : ( left + 1 ); else return -1; }
首先应该明白isB函数的功能,它对于空树返回0,对于平衡树返回树的深度,对于不平衡树返回-1。明白了函数的功能再看代码就明白多了,只要有一个函数返回了-1,则整个函数就会返回-1。
对于递归,最好的理解方式便是从函数的功能意义的层面来理解。了解一个问题如何被分解为它的子问题,这样对于递归函数代码也就理解了。这里有一个误区(我也曾深陷其中),就是通过分析堆栈,分析一个一个函数的调用过程、输出结果来分析递归的算法。这是十分要不得的,这样只会把自己弄晕,其实递归本质上也是函数的调用,调用的函数是自己或者不是自己其实没什么区别。在函数调用时总会把一些临时信息保存到堆栈,堆栈只是为了函数能正确的返回,仅此而已。我们只要知道递归会导致大量的函数调用,大量的堆栈操作就可以了。
小结
递归的基本思想是把规模大的问题转化为规模小的相似的子问题来解决。在函数实现时,因为解决大问题的方法和解决小问题的方法往往是同一个方法,所以就产生了函数调用它自身的情况。另外这个解决问题的函数必须有明显的结束条件,这样就不会产生无限递归的情况了。
http://www.nowamagic.net/librarys/veda/detail/2315
很多人对递归的理解不太深刻。一直就停留在“自己调用自己”的程度上。这其实这只是递归的表象(严格来说连表象都概括得不全面,因为除了“自己调用自己”的递归外,还有交互调用的递归)。而递归的思想远不止这么简单。
递归,并不是简单的“自己调用自己”,也不是简单的“交互调用”。它是一种分析和解决问题的方法和思想。简单来说,递归的思想就是:把问题分解成为规模更小的、具有与原问题有着相同解法的问题。比如二分查找算法,就是不断地把问题的规模变小(变成原问题的一半),而新问题与原问题有着相同的解法。
有些问题使用传统的迭代算法是很难求解甚至无解的,而使用递归却可以很容易的解决。比如汉诺塔问题。但递归的使用也是有它的劣势的,因为它要进行多层函数调用,所以会消耗很多堆栈空间和函数调用时间。
既然递归的思想是把问题分解成为规模更小且与原问题有着相同解法的问题,那么是不是这样的问题都能用递归来解决呢?答案是否定的。并不是所有问题都能用递归来解决。那么什么样的问题可以用递归来解决呢?一般来讲,能用递归来解决的问题必须满足两个条件:
- 可以通过递归调用来缩小问题规模,且新问题与原问题有着相同的形式。
- 存在一种简单情境,可以使递归在简单情境下退出。
如果一个问题不满足以上两个条件,那么它就不能用递归来解决。
为了方便理解,还是拿斐波那契数列来说下:求斐波那契数列的第N项的值。
这是一个经典的问题,说到递归一定要提到这个问题。斐波那契数列这样定义:f(0) = 0, f(1) = 1, 对n > 1, f(n) = f(n-1) + f(n-2)
这是一个明显的可以用递归解决的问题。让我们来看看它是如何满足递归的两个条件的:
- 对于一个n>2, 求f(n)只需求出f(n-1)和f(n-2),也就是说规模为n的问题,转化成了规模更小的问题;
- 对于n=0和n=1,存在着简单情境:f(0) = 0, f(1) = 1。
因此,我们可以很容易的写出计算费波纳契数列的第n项的递归程序:
int fib( n ) { if ( n == 0 ) return 0; else if ( n == 1 ) return 1; else return f( n - 1 ) + f( n - 2 ); }
在编写递归调用的函数的时候,一定要把对简单情境的判断写在最前面,以保证函数调用在检查到简单情境的时候能够及时地中止递归,否则,你的函数可能会永不停息的在那里递归调用了。
http://www.nowamagic.net/librarys/veda/detail/2316
前面谈到了递归的一些思想,还有概念上的一些理解,这里试着用递归解决一些问题。比如回文。
回文是一种字符串,它正着读和反着读都是一样的。比如level,eye都是回文。用迭代的方法可以很快地判断一个字符串是否为回文。用递归的方法如何来实现呢?
首先我们要考虑使用递归的两个条件:
- 第一:这个问题是否可以分解为形式相同但规模更小的问题?
- 第二:如果存在这样一种分解,那么这种分解是否存在一种简单情境?
先来看第一点,是否存在一种符合条件的分解。容易发现,如果一个字符串是回文,那么在它的内部一定存在着更小的回文。 比如level里面的eve也是回文。 而且,我们注意到,一个回文的第一个字符和最后一个字符一定是相同的。
所以我们很自然的有这样的方法:
先判断给定字符串的首尾字符是否相等,若相等,则判断去掉首尾字符后的字符串是否为回文,若不相等,则该字符串不是回文。
注意,我们已经成功地把问题的规模缩小了,去掉首尾字符的字符串当然比原字符串小。
接着再来看第二点, 这种分解是否存在一种简单情境呢?简单情境在使用递归的时候是必须的,否则你的递归程序可能会进入无止境的调用。
对于回文问题,我们容易发现,一个只有一个字符的字符串一定是回文,所以,只有一个字符是一个简单情境,但它不是唯一的简单情境,因为空字符串也是回文。这样,我们就得到了回文问题的两个简单情境:字符数为1和字符数为0。
好了,两个条件都满足了,基于以上分析,我们可以很容易的编写出解决回文问题的递归实现方式:
#include "stdio.h" #include "string.h" int main( void ) { int n, rs; char str[ 50 ]; printf( "请输入需要判断回文的字符串:" ); scanf( "%s", &str ); n = (int) strlen( str ); rs = is_palindereme( str, n ); printf( "%d ", rs ); } int is_palindereme( char *str, int n ) { printf( "Length: %d \n", n ); printf( "%c ----- %c\n", str[ 0 ], str[ n - 1 ] ); if ( n == 0 || n == 1 ) return 1; else { //printf("%d, %d\n", str[0], str[n-1]); return ( ( str[ 0 ] == str[ n - 1 ] ) ? is_palindereme( str + 1, n - 2 ) : 0 ); } }
请输入需要判断回文的字符串:level Length: 5 l ----- l Length: 3 e ----- e Length: 1 v ----- v 1
http://www.nowamagic.net/librarys/veda/detail/2317
还有一个典型的递归例子是对已排序数组的二分查找算法。
现在有一个已经排序好的数组,要在这个数组中查找一个元素,以确定它是否在这个数组中,很一般的想法是顺序检查每个元素,看它是否与待查找元素相同。这个方法很容易想到,但它的效率不能让人满意,它的复杂度是O(n)的。现在我们来看看递归在这里能不能更有效。
还是考虑上面的两个条件:
- 第一:这个问题是否可以分解为形式相同但规模更小的问题?
- 第二:如果存在这样一种分解,那么这种分解是否存在一种简单情境?
考虑条件一:我们可以这样想,如果想把问题的规模缩小,我们应该做什么?
可以的做法是:我们先确定数组中的某些元素与待查元素不同,然后再在剩下的元素中查找,这样就缩小了问题的规模。那么如何确定数组中的某些元素与待查元素不同呢? 考虑到我们的数组是已经排序的,我们可以通过比较数组的中值元素和待查元素来确定待查元素是在数组的前半段还是后半段。这样我们就得到了一种把问题规模缩小的方法。
接着考虑条件二:简单情境是什么呢?
容易发现,如果中值元素和待查元素相等,就可以确定待查元素是否在数组中了,这是一种简单情境,那么它是不是唯一的简单情境呢? 考虑元素始终不与中值元素相等,那么我们最终可能得到了一个无法再分的小规模的数组,它只有一个元素,那么我们就可以通过比较这个元素和待查元素来确定最后的结果。这也是一种简单情境。
好了,基于以上的分析,我们发现这个问题可以用递归来解决,二分法的代码如下:
#include "stdio.h" #include "stdlib.h" void selectionSort( int data[ ], int count ); int binary_search( int *a, int n, int key ); void main( ) { int i, key, rs; int arr[ 10 ]; int count; printf( "排序前数组为:" ); srand( (int) time( 0 ) ); for ( i = 0; i < 10; i++ ) { arr[ i ] = rand( ) % 100; printf( "%d ", arr[ i ] ); } count = sizeof( arr ) / sizeof( arr[ 0 ] ); selectionSort( arr, count ); printf( "\n排序后数组为:" ); for ( i = 0; i < 10; i++ ) { printf( "%d ", arr[ i ] ); } printf( "\n请输入要查找的数字:" ); scanf( "%d", &key ); rs = binary_search( arr, 10, key ); printf( "%d ", rs ); } void selectionSort( int data[ ], int count ) { int i, j, min, temp; for ( i = 0; i < count; i++ ) { /*find the minimum*/ min = i; for ( j = i + 1; j < count; j++ ) if ( data[ j ] < data[ min ] ) min = j; temp = data[ i ]; data[ i ] = data[ min ]; data[ min ] = temp; } } int binary_search( int *data, int n, int key ) { int mid; if ( n == 1 ) { return ( data[ 0 ] == key ); } else { mid = n / 2; printf( "mid=%d\n", data[ mid ] ); if ( data[ mid - 1 ] == key ) return 1; else if ( data[ mid - 1 ] > key ) { printf( "key %d 比 data[mid-1] %d 小,取前半段 \n", key, data[ mid - 1 ] ); return binary_search( &data[ 0 ], mid, key ); } else { printf( "key %d 比 data[mid-1] %d 大,取后半段 \n", key, data[ mid - 1 ] ); return binary_search( &data[ mid ], n - mid, key ); } } }
排序前数组为:53 27 26 99 20 17 15 25 23 63 排序后数组为:15 17 20 23 25 26 27 53 63 99 请输入要查找的数字:20 mid=26 key 20 比 data[mid-1] 25 小,取前半段 mid=20 key 20 比 data[mid-1] 17 大,取后半段 mid=23 1
这个算法的复杂度是O(logn)的,显然要优于先前提到的朴素的顺序查找法。
http://www.nowamagic.net/librarys/veda/detail/2321
递归在解决某些问题的时候使得我们思考的方式得以简化,代码也更加精炼,容易阅读。那么既然递归有这么多的优点,我们是不是什么问题都要用递归来解决呢?难道递归就没有缺点吗?今天我们就来讨论一下递归的不足之处。谈到递归就不得不面对它的效率问题。
为什么递归是低效的
还是拿斐波那契(Fibonacci)数列来做例子。在很多教科书或文章中涉及到递归或计算复杂性的地方都会将计算斐波那契数列的程序作为经典示例。如果现在让你以最快的速度用C#写出一个计算斐波那契数列第n个数的函数(不考虑参数小于1或结果溢出等异常情况),我不知你的程序是否会和下列代码类似:
public static ulong Fib( ulong n ) { return ( n == 1 || n == 2 ) ? 1 : Fib( n - 1 ) + Fib( n - 2 ); }
这段代码应该算是短小精悍(执行代码只有一行),直观清晰,而且非常符合许多程序员的代码美学,许多人在面试时写出这样的代码可能心里还会暗爽。但是如果用这段代码试试计算Fib(1000)我想就再也爽不起来了,它的运行时间也许会让你抓狂。
看来好看的代码未必中用,如果程序在效率不能接受那美观神马的就都是浮云了。如果简单分析一下程序的执行流,就会发现问题在哪,以计算Fibonacci(5)为例:
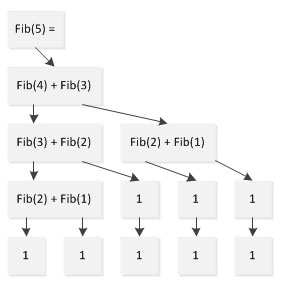
从上图可以看出,在计算Fib(5)的过程中,Fib(1)计算了两次、Fib(2)计算了3次,Fib(3)计算了两次,本来只需要5次计算就可以完成的任务却计算了9次。这个问题随着规模的增加会愈发凸显,以至于Fib(1000)已经无法再可接受的时间内算出。
我们当时使用的是简单的用定义来求 fib(n),也就是使用公式 fib(n) = fib(n-1) + fib(n-2)。这样的想法是很容易想到的,可是仔细分析一下我们发现,当调用fib(n-1)的时候,还要调用fib(n-2),也就是说fib(n-2)调用了两次,同样的道理,调用f(n-2)时f(n-3)也调用了两次,而这些冗余的调用是完全没有必要的。可以计算这个算法的复杂度是指数级的。
改进的斐波那契递归算法
那么计算斐波那契数列是否有更好的递归算法呢? 当然有。让我们来观察一下斐波那契数列的前几项:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55 …
注意到没有,如果我们去掉前面一项,得到的数列依然满足f(n) = f(n-1) – f(n-2), (n>2),而我们得到的数列是以1,2开头的。很容易发现这个数列的第n-1项就是原数列的第n项。怎么样,知道我们该怎么设计算法了吧?我们可以写这样的一个函数,它接受三个参数,前两个是数列的开头两项,第三个是我们想求的以前两个参数开头的数列的第几项。
int fib_i(int a, int b, int n);
在函数内部我们先检查n的值,如果n为3则我们只需返回a+b即可,这是简单情境。如果n>3,那么我们就调用f(b, a+b, n-1),这样我们就缩小了问题的规模(从求第n项变成求第n-1项)。好了,最终代码如下:
int fib_i( int a, int b, int n ) { if ( n == 3 ) return a + b; else return fib_i( b, a + b, n - 1 ); }
这样得到的算法复杂度是O(n)的。已经是线性的了。它的效率已经可以与迭代算法的效率相比了,但由于还是要反复的进行函数调用,还是不够经济。
递归与迭代的效率比较
我们知道,递归调用实际上是函数自己在调用自己,而函数的调用开销是很大的,系统要为每次函数调用分配存储空间,并将调用点压栈予以记录。而在函数调用结束后,还要释放空间,弹栈恢复断点。所以说,函数调用不仅浪费空间,还浪费时间。
这样,我们发现,同一个问题,如果递归解决方案的复杂度不明显优于其它解决方案的话,那么使用递归是不划算的。因为它的很多时间浪费在对函数调用的处理上。在C++中引入了内联函数的概念,其实就是为了避免简单函数内部语句的执行时间小于函数调用的时间而造成效率降低的情况出现。在这里也是一个道理,如果过多的时间用于了函数调用的处理,那么效率显然高不起来。
举例来说,对于求阶乘的函数来说,其迭代算法的时间复杂度为O(n):
int fact( n ) { int i; int r = 1; for ( i = 1; i <= n; i++ ) { r *= i; } return r; }
而其递归函数的时间复杂度也是O(n):
int fact_r( n ) { if ( n == 0 ) return 1; else return n * f( n ); }
但是递归算法要进行n次函数调用,而迭代算法则只需要进行n次迭代而已。其效率上的差异是很显著的。
小结
由以上分析我们可以看到,递归在处理问题时要反复调用函数,这增大了它的空间和时间开销,所以在使用迭代可以很容易解决的问题中,使用递归虽然可以简化思维过程,但效率上并不合算。效率和开销问题是递归最大的缺点。
虽然有这样的缺点,但是递归的力量仍然是巨大而不可忽视的,因为有些问题使用迭代算法是很难甚至无法解决的(比如汉诺塔问题)。这时递归的作用就显示出来了。
递归的效率问题暂时讨论到这里。后面会介绍到递归计算过程与迭代计算过程,讲解得更详细点。
http://www.nowamagic.net/librarys/veda/detail/2322
所谓的递归慢到底是什么原因呢?
前面一篇讲到了递归的效率问题,但是没具体深入到数据结构层面的解释,这里补充一下。
大家都知道递归的实现是通过调用函数本身,函数调用的时候,每次调用时要做地址保存,参数传递等,这是通过一个递归工作栈实现的。具体是每次调用函数本身要保存的内容包括:局部变量、形参、调用函数地址、返回值。那么,如果递归调用N次,就要分配N*局部变量、N*形参、N*调用函数地址、N*返回值。这势必是影响效率的。
递归是利用系统的堆栈保存函数当中的局部变量来解决问题的。递归说白了就是在栈处理栈上一堆的指针指向内存中的对象,这些对象一直不被释放,直到递归执行到最后一次跳出条件的时候,才一个个出栈。所以开销很大。
用循环效率会比递归效率高吗?
递归与循环是两种不同的解决问题的典型思路。当然也并不是说循环效率就一定比递归高,递归和循环是两码事,递归带有栈操作,循环则不一定,两个概念不是一个层次,不同场景做不同的尝试。
1. 递归算法:
- 优点:代码简洁、清晰,并且容易验证正确性。(如果你真的理解了算法的话,否则你更晕)
- 缺点:它的运行需要较多次数的函数调用,如果调用层数比较深,需要增加额外的堆栈处理(还有可能出现堆栈溢出的情况),比如参数传递需要压栈等操作,会对执行效率有一定影响。但是,对于某些问题,如果不使用递归,那将是极端难看的代码。
2. 循环算法:
- 优点:速度快,结构简单。
- 缺点:并不能解决所有的问题。有的问题适合使用递归而不是循环。如果使用循环并不困难的话,最好使用循环。
3. 递归算法和循环算法总结:
递归通常很直白地描述了一个求解过程,因此也是最容易被想到和实现的算法。循环其实和递归具有相同的特性(即:做重复任务),但有时,使用循环的算法并不会那么清晰地描述解决问题步骤。单从算法设计上看,递归和循环并无优劣之别。然而,在实际开发中,因为函数调用的开销,递归常常会带来性能问题,特别是在求解规模不确定的情况下。而循环因为没有函数调用开销,所以效率会比递归高。除少数编程语言对递归进行了优化外,大部分语言在实现递归算法时还是十分笨拙,由此带来了如何将递归算法转换为循环算法的问题。算法转换应当建立在对求解过程充分理解的基础上,有时甚至需要另辟蹊径。
- 一般递归调用可以处理的算法,也通过循环去解决需要额外的低效处理。
- 现在的编译器在优化后,对于多次调用的函数处理会有非常好的效率优化,效率未必低于循环。
- 递归和循环两者完全可以互换。如果用到递归的地方可以很方便使用循环替换,而不影响程序的阅读,那么替换成递归往往是好的。(例如:求阶乘的递归实现与循环实现。)
要转换成为非递归,两步工作:
- 第一步,可以自己建立一个堆栈保存这些局部变量,替换系统栈;
- 第二步把对递归的调用转变为循环处理就可以了。
那么递归使用的栈是什么样的一个栈呢?
首先,看一下系统栈和用户栈的用途。
- 系统栈(也叫核心栈、内核栈)是内存中属于操作系统空间的一块区域,其主要用途为:
- 保存中断现场,对于嵌套中断,被中断程序的现场信息依次压入系统栈,中断返回时逆序弹出;
- 保存操作系统子程序间相互调用的参数、返回值、返回点以及子程序(函数)的局部变量。
- 用户栈是用户进程空间中的一块区域,用于保存用户进程的子程序间相互调用的参数、返回值、返回点以及子程序(函数)的局部变量。
我们编写的递归程序属于用户程序,因此使用的是用户栈。
http://www.nowamagic.net/librarys/veda/detail/2324
先摘抄“为之漫笔”对这几个概念的一段理解:
loop、iterate、traversal和recursion这几个词是计算机技术书中经常会出现的几个词汇。众所周知,这几个词分别翻译为:循环、迭代、遍历和递归。乍一看,这几个词好像都与重复(repeat)有关,但有的又好像不完全是重复的意思。那么这几个词到底各是什么含义,有什么区别和联系呢?下面就试着解释一下。
- 循环(loop),指的是在满足条件的情况下,重复执行同一段代码。比如,while语句。
- 迭代(iterate),指的是按照某种顺序逐个访问列表中的每一项。比如,for语句。
- 遍历(traversal),指的是按照一定的规则访问树形结构中的每个节点,而且每个节点都只访问一次。
- 递归(recursion),指的是一个函数不断调用自身的行为。比如,以编程方式输出著名的斐波纳契数列。
有了以上定义,这几个概念之间的区别其实就比较清楚了。至于它们之间的联系,严格来讲,它们似乎都属于算法的范畴。换句话说,它们只不过是解决问题的不同手段和方式,而本质上则都是计算机编程中达成特定目标的途径。
迭代
迭代算法是用计算机解决问题的一种基本方法。它利用计算机运算速度快、适合做重复性操作的特点,让计算机对一组指令(或一定步骤)进行重复执行,在每次执行这组指令(或这些步骤)时,都从变量的原值推出它的一个新值。
利用迭代算法解决问题,需要做好以下三个方面的工作:
- 确定迭代变量。在可以用迭代算法解决的问题中,至少存在一个直接或间接地不断由旧值递推出新值的变量,这个变量就是迭代变量。
- 建立迭代关系式。所谓迭代关系式,指如何从变量的前一个值推出其下一个值的公式(或关系)。迭代关系式的建立是解决迭代问题的关键,通常可以使用递推或倒推的方法来完成。
- 对迭代过程进行控制。在什么时候结束迭代过程?这是编写迭代程序必须考虑的问题。不能让迭代过程无休止地重复执行下去。迭代过程的控制通常可分为两种情况:一种是所需的迭代次数是个确定的值,可以计算出来;另一种是所需的迭代次数无法确定。对于前一种情况,可以构建一个固定次数的循环来实现对迭代过程的控制;对于后一种情况,需要进一步分析出用来结束迭代过程的条件。
可以用迭代的算法有很经典的问题,比如兔子产子问题:假定你有一雄一雌一对刚出生的兔子,它们在长到一个月大小时开始交配,在第二月结束时,雌兔子产下另一对兔子,过了一个月后它们也开始繁殖,如此这般持续下去。每只雌兔在开始繁殖时每月都产下一对兔子,假定没有兔子死亡,在一年后总共会有多少对兔子?
还有上楼梯的走法问题:有一段楼梯有10级台阶,规定每一步只能跨一级或两级,要登上第10级台阶有几种不同的走法?
这两个问题可以参看以前写的一篇文章:趣味算法之兔子产子问题
迭代与循环
先从字面上看:
- 迭代:“迭”:轮流,轮番,替换,交替,更换。“代”:代替。所以迭代的意思是:变化的循环,这种变化就是轮番代替,轮流代替。
- 循环:不变的重复。
个人认为迭代是循环的一种,循环体代码分为固定循环体,和变化的循环体。
固定的循环举例:
for(i=0; i < 8; i++) { // 'Welcome to NowaMagic'; }
实现迭代:
int sum = 0; for(i = 1; i <= 1000; i++ ) { sum = sum + i; }
上面的迭代是常见的递增式迭代。类似的还有递减式迭代,递乘式迭代。
迭代的好处:迭代减少了冗余代码,提高了代码的利用率和动态性。
循环、迭代与递归
1. 递归算法与迭代算法的设计思路区别在于:函数或算法是否具备收敛性,当且仅当一个算法存在预期的收敛效果时,采用递归算法才是可行的,否则,就不能使用递归算法。
当然,从理论上说,所有的递归函数都可以转换为迭代函数,反之亦然,然而代价通常都是比较高的。但从算法结构来说,递归声明的结构并不总能够转换为迭代结构,原因在于结构的引申本身属于递归的概念,用迭代的方法在设计初期根本无法实现,这就像动多态的东西并不总是可以用静多态的方法实现一样。这也是为什么在结构设计时,通常采用递归的方式而不是采用迭代的方式的原因,一个极典型的例子类似于链表,使用递归定义及其简单,但对于内存定义(数组方式)其定义及调用处理说明就变得很晦涩,尤其是在遇到环链、图、网格等问题时,使用迭代方式从描述到实现上都变得很不现实。
2. 递归其实是方便了程序员难为了机器。它只要得到数学公式就能很方便的写出程序。优点就是易理解,容易编程。但递归是用栈机制实现的,每深入一层,都要占去一块栈数据区域,对嵌套层数深的一些算法,递归会力不从心,空间上会以内存崩溃而告终,而且递归也带来了大量的函数调用,这也有许多额外的时间开销。所以在深度大时,它的时空性就不好了。
循环其缺点就是不容易理解,编写复杂问题时困难。优点是效率高。运行时间只因循环次数增加而增加,没什么额外开销。空间上没有什么增加。
3. 局部变量占用的内存是一次性的,也就是O(1)的空间复杂度,而对于递归(不考虑尾递归优化的情况),每次函数调用都要压栈,那么空间复杂度是O(n),和递归次数呈线性关系。
4. 递归程序改用循环实现的话,一般都是要自己维护一个栈的,以便状态的回溯。如果某个递归程序改用循环的时候根本就不需要维护栈,那其实这个递归程序这样写只是意义明显一些,不一定要写成递归形式。但很多递归程序就是为了利用函数自身在系统栈上的auto变量记录状态,以便回溯。
原理上讲,所有递归都是可以消除的,代价就是可能自己要维护一个栈。而且我个人认为,很多情况下用递归还是必要的,它往往能把复杂问题分解成更为简单的步骤,而且很能反映问题的本质。
递归其实就是利用系统堆栈,实现函数自身调用,或者是相互调用的过程。在通往边界的过程中,都会把单步地址保存下来,知道等出边界,再按照先进后出的进行运算,这正如我们装木桶一样,每一次都只能把东西方在最上面,而取得时候,先放进取的反而最后取出。递归的数据传送也类似。但是递归不能无限的进行下去,必须在一定条件下停止自身调用,因此它的边界值应是明确的。就向我们装木桶一样,我们不能总是无限制的往里装,必须在一定的时候把东西取出来。比较简单的递归过程是阶乘函数,你可以去看一下。但是递归的运算方法,往往决定了它的效率很低,因为数据要不断的进栈出栈。
但是递归作为比较基础的算法,它的作用不能忽视。
纯粹个人见解,如有不同看法,欢迎联系我讨论。
http://www.nowamagic.net/librarys/veda/detail/2280
最近重新看SICP,写点感想。下面是关于递归与迭代计算的一些知识,SICP 1.2.1。
递归
递归是实现程序计算过程中的描述过程的基本模式之一,在讨论递归的问题前我们必须十分小心,因为递归包含两个方面的内容,一个是递归的计算过程,一个是递归过程,后者是语法上的事实而前者是概念上的计算过程,事实上在程序上我们也许是使用循环来实现的。
递归计算过程和我们常说的递归过程不是一回事。
- 递归过程:“当我们说一个过程是递归的时候,论述的是一个语法形式上的事实,说明这个过程的定义中(直接或者间接地)引用了该过程本身。”
- 递归计算过程:“在说某一计算过程具有某种模式时(例如,线性递归),我们说的是这一计算过程的进展方式, 而不是相应过程书写上的语法形式。”
一般在讨论递归的时候都喜欢用斐波那契数列来作为例子,斐波那契的算法也很简单,算法如下:
#include "stdio.h" #include "math.h" int factorial( int n ); int main( void ) { int i, n, rs; printf( "请输入斐波那契数n:" ); scanf( "%d", &n ); for ( i = 1; i <= n; i++ ) { rs = factorial( i ); printf( "%d ", rs ); } return 0; } // 递归计算过程 int factorial( int n ) { if ( n <= 2 ) { return 1; } else { return factorial( n - 1 ) + factorial( n - 2 ); } }
请输入斐波那契数n:12 1 1 2 3 5 8 13 21 34 55 89 144
我们假设n=6,那么得到的计算过程就是,要计算Fib(6)就得计算Fib(5)和Fib(4),以此类推,如下图:
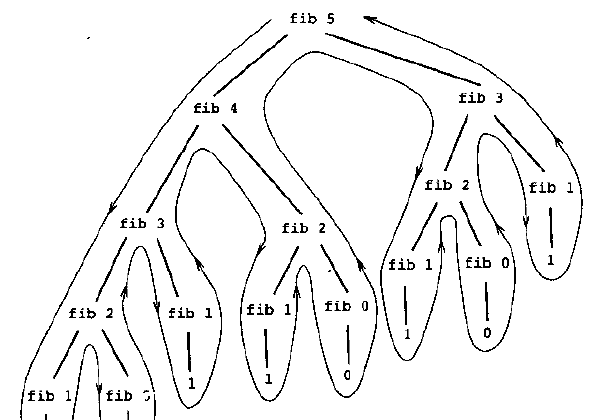
我们可以看到过程如同一棵倒置的树,这种方式被称之为树形递归,也被称之为线性递归。这种递归的方式非常的直白,很好理解其计算过程,一般很多人写递归都会下意识的采用这种方式。
但是缺点也是很明显的,从其计算过程可以看出,经过了很多冗余的计算,并且消耗了大量的调用堆栈,这个消耗是指数级增长的,经常有人说调用堆栈很容易在很短的递归过程就耗光了,多半就是采用了线性递归造成的。线性递归的过程可用下图描述,可以清晰的看到展开收拢的过程:
1 (factorial (6)) 2 (6 * factorial (5)) 3 (6 * (5 * factorial (4))) 4 (6 * (5 * (4 * factorial (3)))) 5 (6 * (5 * (4 * (3 * factorial (2))))) 6 (6 * (5 * (4 * (3 * (2 * factorial (1)))))) 7 (6 * (5 * (4 * (3 * (2 * 1))))) 8 (6 * (5 * (4 * (3 * 2)))) 9 (6 * (5 * (4 * 6))) 10 (6 * (5 * 24)) 11 (6 * 120) 12 720
迭代
与递归计算过程相对应的,是迭代计算过程。
除了这种递归方式还有另外一种实现递归的方式,同样是上面的斐波那契数作为例子,这次我们不按照斐波那契的定义入手,我们从正常产生数列的过程入手来实现,0,1,的情况很简单可以直接返回,之后的计算过程就是累加,我们在递归的过程中要保持状态,这个状态要保持三个数,也就是上两个数和迭代的步数,所以我们定义的方法为:
def Fib(n,b1=1,b2=1,c=3):
if n <= 2:
return 1
else:
if n==c:
return b1+b2
else:
return Fib(n,b1=b2,b2=b1+b2,c=c+1)
这种方法我们在每一次递归的过程中保持了上一次计算的状态,所以称之为“线性迭代过程”,也就是俗称的尾递归。由于每一步计算都保持了状态所以消除了冗余计算,所以这种方式的效率明显高于前一种,其计算过程如下:
1 fib(6) 2 fib 0,0,1 3 fib 0,1,2 4 fib 1,2,3 5 fib 2,3,4 6 fib 3,5,5 7 fib 5,8,6
这两种递归方式之间是可以转换的,凡是可以通过固定数量状态来描述中间计算过程的递归过程都可以通过线性迭代来表示。
“迭代计算过程是用固定数目的状态变量描述的计算过程,并存在着一套固定的规则,描述了计算过程从一个状态到下一状态转换时,这些变量的更新方式,还有一个(可能有的)结束检测,它描述这一计算过程应该中止的条件。”
以计算n的阶乘为例,其递归写为:
// 递归计算过程 int factorial( n ) { if ( n == 1 ) { return 1; } return n * f( n - 1 ); }
样是计算n的阶乘,还可以这样设计:
// 迭代计算过程 int factorial( int n ) { return factIterator( 1, 1, n ); } int factIterator( int result, int counter, int maxCount ) { if ( counter > maxCount ) { return result; } return factIterator( ( counter * result ), counter + 1, maxCount ); }
1 (factorial (6)) 2 (factIterator(1, 1, 6)) 3 (factIterator(1, 2, 6)) 4 (factIterator(2, 3, 6)) 5 (factIterator(6, 4, 6)) 6 (factIterator(24, 5, 6)) 7 (factIterator(120, 6, 6)) 8 (factIterator(720, 7, 6))
虽然factIterator方法调用了它自己,但从它的执行过程里,所需要的所有的东西就是result,counter,和maxCount。所以它是迭代计算过程。这个过程在继续调用自身时不需要增加存储,这样的过程叫尾递归。
尾递归还可以用循环来代替:
function fib(n){ var a=0, b=1; for(var i=0;i<=n;i++){ var temp = a+b; a = b; b = temp; } return b; }
递归和迭代
递归计算过程更自然,更直截了当,可以帮助我们理解和设计程序。而要规划出一个迭代计算过程,则需设计出各个状态变量,找到迭代规律,并不是所有的递归计算过程都可以很容易的整理成迭代计算过程。
但递归计算过程会比迭代计算过程低效。
上面计算阶乘的递归计算过程属于线性递归,步骤数目的增长正比于输入n。也就是说,这个过程所需步骤的增长为O(n) ,空间需求的增长也为O(n) 。对于迭代的阶乘,步数还是O(n)而空间是O(1) ,也就是常数。
再来看斐波那契数列的递归与迭代的实现吧。
递归计算过程:
// 递归计算过程 function fib(n){ if(n <= 1){ return n; } return fib(n-1) + fib(n-2); }
迭代计算过程、尾递归:
// 迭代计算过程、尾递归 function fib(n){ return fibIterator(1, 0, n); } function fibIterator(a, b, counter){ if(counter== 0){ return b; } return fibIterator((a+b), a, counter-1) }
斐波那契数列的递归计算过程属于树形递归,画一下它的展开方式就可以看到。它的步数是以指数方式增长的,这是一种非常夸张的增长方式,规模每增加1,都将导致所用的资源按照某个常数倍增长。而迭代计算过程的步骤增长依然是O(n),线性增长,也就是规模增长一倍,所用的资源也增加一倍。
有时候说要减少递归,就是要减少递归计算过程,用更高效的方法代替。
我们也发现,其实尾递归的过程和循环基本上是等价的,我们可以将尾递归的过程很方便到用循环来代替,所以很多的语言对尾递归提供了编译级别的优化,也就是将尾递归在编译期转化成循环的代码。不过对于没有提供尾递归优化的语言来说也是很有意义的,比如python的默认调用堆栈长度是1000,如果用线性递归很快就会消耗光,但是尾递归就不会,比如尾递归的Fib函数,用Fib(1001)调用没问题的而且跑得飞快,Fib(1002)的时候才堆栈溢出。但是如果是线性递归的方式计算n=30的时候就能明显感觉到速度变慢,40以上基本就挂了。
这里我无意对比两种方式的优劣,也许线性递归性能有差距但是它的可读性非常的强,几乎就等同于公式的直接描述,所以可以根据计算规模来合理选用。
http://www.nowamagic.net/librarys/veda/detail/2325
尾递归(tail recursive),看名字就知道是某种形式的递归。简单的说递归就是函数自己调用自己。那尾递归和递归之间的差别就只能体现在参数上了。
尾递归wiki解释如下:
尾部递归是一种编程技巧。递归函数是指一些会在函数内调用自己的函数,如果在递归函数中,递归调用返回的结果总被直接返回,则称为尾部递归。尾部递归的函数有助将算法转化成函数编程语言,而且从编译器角度来说,亦容易优化成为普通循环。这是因为从电脑的基本面来说,所有的循环都是利用重复移跳到代码的开头来实现的。如果有尾部归递,就只需要叠套一个堆栈,因为电脑只需要将函数的参数改变再重新调用一次。利用尾部递归最主要的目的是要优化,例如在Scheme语言中,明确规定必须针对尾部递归作优化。可见尾部递归的作用,是非常依赖于具体实现的。
我们还是从简单的斐波那契开始了解尾递归吧。
用普通的递归计算Fibonacci数列:
#include "stdio.h" #include "math.h" int factorial( int n ); int main( void ) { int i, n, rs; printf( "请输入斐波那契数n:" ); scanf( "%d", &n ); rs = factorial( n ); printf( "%d \n", rs ); return 0; } // 递归 int factorial( int n ) { if ( n <= 2 ) { return 1; } else { return factorial( n - 1 ) + factorial( n - 2 ); } }
程序员运行结果如下:
1 2 3 4 5 | 请输入斐波那契数n:206765Process returned 0 (0x0) execution time : 3.502 sPress any key to continue. |
在i5的CPU下也要花费 3.502 秒的时间。
下面我们看看如何用尾递归实现斐波那契数。
#include "stdio.h" #include "math.h" int factorial( int n ); int main( void ) { int i, n, rs; printf( "请输入斐波那契数n:" ); scanf( "%d", &n ); rs = factorial_tail( n, 1, 1 ); printf( "%d ", rs ); return 0; } int factorial_tail( int n, int acc1, int acc2 ) { if ( n < 2 ) { return acc1; } else { return factorial_tail( n - 1, acc2, acc1 + acc2 ); } }
请输入斐波那契数n:20 6765 Process returned 0 (0x0) execution time : 1.460 s Press any key to continue.
快了一倍有多。当然这是不完全统计,有兴趣的话可以自行计算大规模的值,这里只是介绍尾递归而已。
我们可以打印一下程序的执行过程,函数加入下面的打印语句:
int factorial_tail( int n, int acc1, int acc2 ) { if ( n < 2 ) { return acc1; } else { printf( "factorial_tail(%d, %d, %d) \n", n - 1, acc2, acc1 + acc2 ); return factorial_tail( n - 1, acc2, acc1 + acc2 ); } }
1 请输入斐波那契数n:10 2 factorial_tail(9, 1, 2) 3 factorial_tail(8, 2, 3) 4 factorial_tail(7, 3, 5) 5 factorial_tail(6, 5, 8) 6 factorial_tail(5, 8, 13) 7 factorial_tail(4, 13, 21) 8 factorial_tail(3, 21, 34) 9 factorial_tail(2, 34, 55) 10 factorial_tail(1, 55, 89) 11 55 12 Process returned 0 (0x0) execution time : 1.393 s 13 Press any key to continue.
从上面的调试就可以很清晰地看出尾递归的计算过程了。acc1就是第n个数,而acc2就是第n与第n+1个数的和,这就是我们前面讲到的“迭代”的精髓,计算结果参与到下一次的计算,从而减少很多重复计算量。
fibonacci(n-1,acc2,acc1+acc2)真是神来之笔,原本朴素的递归产生的栈的层次像二叉树一样,以指数级增长,但是现在栈的层次却像是数组,变成线性增长了,实在是奇妙,总结起来也很简单,原本栈是先扩展开,然后边收拢边计算结果,现在却变成在调用自身的同时通过参数来计算。
小结
尾递归的本质是:将单次计算的结果缓存起来,传递给下次调用,相当于自动累积。
在Java等命令式语言中,尾递归使用非常少见,因为我们可以直接用循环解决。而在函数式语言中,尾递归却是一种神器,要实现循环就靠它了。
很多人可能会有疑问,为什么尾递归也是递归,却不会造成栈溢出呢?因为编译器通常都会对尾递归进行优化。编译器会发现根本没有必要存储栈信息了,因而会在函数尾直接清空相关的栈。
http://www.nowamagic.net/librarys/veda/detail/2331
复习下尾递归
与普通递归相比,由于尾递归的调用处于方法的最后,因此方法之前所积累下的各种状态对于递归调用结果已经没有任何意义,因此完全可以把本次方法中留在堆栈中的数据完全清除,把空间让给最后的递归调用。这样的优化便使得递归不会在调用堆栈上产生堆积,意味着即时是“无限”递归也不会让堆栈溢出。这便是尾递归的优势。
有些朋友可能已经想到了,尾递归的本质,其实是将递归方法中的需要的“所有状态”通过方法的参数传入下一次调用中。
在上一篇文章里,普通递归是这样的:
// 递归 int factorial( int n ) { if ( n <= 2 ) { return 1; } else { return factorial( n - 1 ) + factorial( n - 2 ); } }
而改造成尾递归,我们则需要提供两个累加器:
int factorial_tail( int n, int acc1, int acc2 ) { if ( n < 2 ) { return acc1; } else { return factorial_tail( n - 1, acc2, acc1 + acc2 ); } }
于是在调用时,需要提供两个累加器的初始值:factorial_tail(n, 1, 1)
Continuation Passing Style的概念
说起Continuation,像我这样的大多数从C, Basic, Pascal起步的程序员可能都不清楚。但是这个概念在functional language 社区却好象是常识一样,很多人在讨论问题的时候总是假设你已经知道了continuation的基本概念,什么Call-CC什么的都不加解释就直接引用。于是,如果不知道continuation到底指的是什么,简直就无法理解他们在说什么。
所谓continuation,其实本来是一个函数调用机制。
我们熟悉的函数调用方法都是使用堆栈,采用Activation record或者叫Stack frame来记录从最顶层函数到当前函数的所有context。一个frame/record就是一个函数的局部上下文信息,包括所有的局部变量的值和SP, PC指针的值(通过静态分析,某些局部变量的信息是不必保存的,特殊的如尾调用的情况则不需要任何stack frame。不过,逻辑上,我们认为所有信息都被保存了)。函数的调用前往往伴随着一些push来保存context信息,函数退出时则是取消当前的record/frame,恢复上一个调用者的record/frame。
像pascal这样的支持嵌套函数的,则需要一个额外的指针来保存父函数的frame地址。不过,无论如何,在任何时候,系统保存的就是一个后入先出的堆栈,一个函数一旦退出,它的frame就被删除了。
Continuation则是另一种函数调用方式。它不采用堆栈来保存上下文,而是把这些信息保存在continuation record中。这些continuation record和堆栈的activation record的区别在于,它不采用后入先出的线性方式,所有record被组成一棵树(或者图),从一个函数调用另一个函数就等于给当前节点生成一个子节点,然后把系统寄存器移动到这个子节点。一个函数的退出等于从当前节点退回到父节点。
这些节点的删除是由garbage collection来管理。如果没有引用这个record,则它就是可以被删除的。
这样的调用方式和堆栈方式相比的好处在哪里呢?
最大的好处就是,它可以让你从任意一个节点跳到另一个节点。而不必遵循堆栈方式的一层一层的return方式。比如说,在当前的函数内,你只要有一个其它函数的节点信息,完全可以选择return到那个函数,而不是循规蹈矩地返回到自己的调用者。你也可以在一个函数的任何位置储存自己的上下文信息,然后,在以后某个适当的时刻,从其它的任何一个函数里面返回到自己现在的位置。
Scheme语言有一个CallCC (call with current continuation)的机制,也就是说:取得当前的continuation,传递给要call的这个函数,这个函数可以选择在适当的时候直接return到当前的continuation。
经典的应用有:exception,back-tracking算法, coroutine等。
应用continuation对付exception是很明显的,只要给可能抛出异常的函数一个外面try的地方的continuation record,这个函数就可以在需要的时候直接返回到try语句的地方。
Exception-handling也可以利用continuation。c++等语言普遍采用的是遇到exception就直接中止当前函数的策略,但是,还有一种策略是允许resume,也就是说,出现了异常之后,有可能异常处理模块修复了错误发生的地方然后选择恢复执行被异常中断了的代码。被异常中断的代码可以取得当前的continuation,传递给异常处理模块,这样当resume的时候可以直接跳到出现异常的地方。Back-tracking算法也可以用类似的方法,在某些地方保存当前的continuation,然后以后就可以从其它的函数跳回当前的语句。
Continuation机制的优化始终不是一个trivial的问题,实际上采取continuation的语言不多。而且,continuation调用方式依赖垃圾收集,也不是c/c++这类中低级的语言所愿意采用的。
不过,continuation的思想仍然是有其用武之地的。有一种设计的风格叫做continuation-passing-style。它的基本思想是:当需要返回某些数据的时候,不是直接把它当作函数的返回值,而是接受一个叫做continuation的参数,这个参数就是一个call-back函数, 它接受这个数据,并做需要做的事情。
举个例子:
x = f();
print x;
把它变成continuation-passing-style, 则是:
f(print);
f()函数不再返回x, 而是接受一个函数,然后把本来要返回的x传递给这个函数。
这个例子也许看上去有点莫名其妙:为什么这么做呢?对Haskell这样的语言,一个原因是:当函数根据不同的输入可能返回不同类型的值时,用返回值的话就必须设计一个额外的数据结构来处理这种不同的可能性。比如:
一个函数f(int)的返回值可能是一个int, 两个float或者三个complex,那么,我们可以这样设计我们的函数f:
f:: int -> (int->a) -> (float->float->a) -> (complex->complex->complex->a) -> a
这个函数接受一个整形参数,三个continuation回调用来处理三种不同的返回情况,最后返回这三个回调所返回的类型。
另一个原因:对模拟imperative风格的monad,可以在函数中间迅速返回(类似于C里面的return或者throw)
对于C++,我想,除了处理不同返回类型的问题,另一个应用可以是避免返回值的不必要拷贝。虽然c++现在有NRV优化,但是这个优化本身就很含混,各个编译器对NRV的实现也不同。C++中的拷贝构造很多时候是具有副作用的,作为程序员,不知道自己写的的副作用到底是否被执行了,被执行了几次,总不是一个舒服事。
而continuation-passing-style,不依赖于任何偏僻的语言特性,也不会引入任何的模棱两可,也许可以作为一个设计时的选择。举个例子, 对于字符串的拼接,如果使用continuation-passing-style如下:
template<class F> void concat(const string& s1, const string& s2, F ret) { string s(s1); s.append(s2); ret(s); //此处,本来应该是return(s),但是我们把它变成ret(s)。 }
我们就可以很安心地说,我们此处没有引入任何不必要的拷贝,不论什么编译器。
当然,continuation style的问题是,它不如直接返回值直观,类型系统也无法保证你确实调用了ret(s)。而且,它需要一个function object,c++又不支持lamda,定义很多trivial的functor也会让程序变得很难看。
利弊如何,还要自己权衡。
尾递归与Continuation Passing Style
我觉得,尾递归其实就是Continuation Passing Style.
Continuation其实就可以看作当前的运行栈。只是我们并不需要整个运行栈,所以,我们可以自己把需要重用的计算结果,都包装在多出来的一个context(contiunation)参数里面,传递下去。 最复杂的情况,这个context也不过是一个stack数据结构。
用例子来说明吧:
1头母牛,出生后第3年,就开始每年生1头母牛,按此规律,第n年时有多少头母牛。
f(1)=1 f(2)=1 f(n)=f(n-1)+f(n-2)
Fibonacci数列:1,1,2,3,5,8,13,,21,34........
稍微将问题再变一下:
1头母牛,出生后第4年,就开始每年生1头母牛,按此规律,第n年时有多少头母牛。
f(1)=1 f(2)=1 f(3)=1 f(n)=f(n-1)+f(n-3)
Fibonacci数列:1, 1, 1, 2, 3, 4, 6, 9,13,19,28........
再将问题一般化,通用描述如下:
1头母牛,出生后第x年,就开始每年生1头母牛,按此规律,第n年时有多少头母牛。
令k = x - 1 f(1)=1 … f(k)=1 f(n)=f(n-1)+f(n-k)
递归解法仍然很自然:
int fibonacci( int n, int k ) { if ( n <= k ) return 1; int previousResult1 = fibonacci( n - 1 ); int previousResultK= fibonacci(n – k); int result = previousResult1 + previousResultK; return result; }
下面把它改成Tail Recursion。这时候我们需要跟踪前k结果。不管怎么说,对于每一次执行,k还是一个固定数字。我们可以用一个k长度的数组来保存前k个中间结果,而不需要一个变长的stack结构。我们可以移动这个k长度的数组里面的数据,来存储当前需要用到的计算结果,参见move方法。(好像一个网络传输协议中的那个窗口概念一样)
int[] alloc(int k) { int[] array = new int[k]; for(int i = 0; i < k; i++) { array[ i ] = 1; } return array; } void move(int[] array) { int k = array.length; int limit = k – 1; for(int i = 0; i < limit; i++) { array[i+1] = array[ i ]; } } int fibonacci( int n, int k ) { int[] middleResults = alloc(k); return tail_recursive_fibonacci(1, middleResults[], n); } int tail_recursive_fibonacci(int currentStep, int[] middleResults, int n) { int k = middleResults.length; if(currentStep <= k) return 1; if(currentStep == n) return middleResults[0] + middleResults[k-1]; int nextStep = currentStep + 1; int currentResult = middleResults[0] + middleResults[k-1]; move(middleResults); middleResults[0] = currentResult; return tail_recursive_fibonacci(nextStep, previousResult1, previousResult2); }
下面我们把它改成循环。关键步骤还是把middleResults作为循环体外部的变量。
int fibonacci( int n, int k ) { if ( n == 1 ) return 1; if ( n == 2 ) return 1; int[] middleResults = alloc(k); int last = k – 1; int result = 0; for ( int i = 3; i <= n; i++ ) { result = middleResults[ 0 ] + middleResults[ last ]; move( middleResults ); middleResults[ 0 ] = result; } return result; }
上述写法采用了最直观的写法,并不是最俭省的写法。比如,tail_recursive_fibonacci函数的currentStep参数可以省掉;循环解法里面的最后一次循环中,计算result后,可以直接break。
http://www.nowamagic.net/librarys/veda/detail/2332
尾递归与Continuation的联系
前面谈了尾递归与Continuation,但是感觉还有些要补充下。
Continuation是一种非常古老的程序结构,简单说来就是entire default future of a computation, 即对程序“接下来要做的事情”所进行的一种建模,即为“完成某件事情”之后“还需要做的事情”。而这种做法,也可以体现在尾递归构造中。
例如以下为阶乘方法的传统递归定义:
int FactorialRecursively( int n ) { if ( n == 0 ) return 1; return FactorialRecursively( n - 1 ) * n; }
显然,这不是一个尾递归的方式,当然我们轻易将其转换为之前提到的尾递归调用方式。不过我们现在把它这样“理解”:每次计算n的阶乘时,其实是“先获取n - 1的阶乘”之后再“与n相乘并返回”,于是我们的FactorialRecursively方法可以改造成:
int FactorialRecursively( int n ) { return FactorialContinuation(n - 1, r => n * r); } // FactorialContinuation(n, x => x) int FactorialContinuation(int n, Func<int, int> continuation) { // ... }
FactorialContinuation方法的含义是“计算n的阶乘,并将结果传入continuation方法,并返回其调用结果”。于是,很容易得出,FactorialContinuation方法自身便是一个递归调用:
public static int FactorialContinuation(int n, Func<int, int> continuation) { return FactorialContinuation(n - 1, r => continuation(n * r)); }
FactorialContinuation方法的实现可以这样表述:“计算n的阶乘,并将结果传入continuation方法并返回”,也就是“计算n - 1的阶乘,并将结果与n相乘,再调用continuation方法”。为了实现“并将结果与n相乘,再调用continuation方法”这个逻辑,代码又构造了一个匿名方法,再次传入FactorialContinuation方法。当然,我们还需要为它补充递归的出口条件:
public static int FactorialContinuation(int n, Func<int, int> continuation) { if (n == 0) return continuation(1); return FactorialContinuation(n - 1, r => continuation(n * r)); }
很明显,FactorialContinuation实现了尾递归。如果要计算n的阶乘,我们需要如下调用FactorialContinuation方法,表示“计算10的阶乘,并将结果直接返回”:
FactorialContinuation(10, x => x)
再加深一下印象,大家是否能够理解以下计算“斐波那契”数列第n项值的写法?
public static int FibonacciContinuation(int n, Func<int, int> continuation) { if (n < 2)
return continuation(n);
return FibonacciContinuation(n - 1, r1 => FibonacciContinuation(n - 2, r2 => continuation(r1 + r2))); }
在函数式编程中,此类调用方式便形成了“Continuation Passing Style(CPS)”。由于C#的Lambda表达式能够轻松构成一个匿名方法,我们也可以在C#中实现这样的调用方式。您可能会想——汗,何必搞得这么复杂,计算阶乘和“斐波那契”数列不是一下子就能转换成尾递归形式的吗?不过,您试试看以下的例子呢?
对二叉树进行先序遍历(pre-order traversal)是典型的递归操作,假设有如下TreeNode类:
public class TreeNode { public TreeNode(int value, TreeNode left, TreeNode right) { this.Value = value; this.Left = left; this.Right = right; } public int Value { get; private set;} public TreeNode Left { get; private set;} public TreeNode Right { get; private set;} }
于是我们来传统的先序遍历一下:
public static void PreOrderTraversal( TreeNode root ) { if ( root == null ) return; Console.WriteLine( root.Value ); PreOrderTraversal( root.Left ); PreOrderTraversal( root.Right ); }
您能用“普通”的方式将它转换为尾递归调用吗?这里先后调用了两次PreOrderTraversal,这意味着必然有一次调用没法放在末尾。这时候便要利用到Continuation了:
public static void PreOrderTraversal(TreeNode root, Action<TreeNode> continuation) { if (root == null) { continuation(null); return; } Console.WriteLine(root.Value); PreOrderTraversal(root.Left, left => PreOrderTraversal(root.Right, right => continuation(right) ) ); }
我们现在把每次递归调用都作为代码的最后一次操作,把接下来的操作使用Continuation包装起来,这样就实现了尾递归,避免了堆栈数据的堆积。可见,虽然使用Continuation是一个略有些“诡异”的使用方式,但是在某些时候它也是必不可少的使用技巧。
Continuation的改进
看看刚才的先序遍历实现,您有没有发现一个有些奇怪的地方?
PreOrderTraversal(root.Left, left => PreOrderTraversal(root.Right, right => continuation(right) ) );
关于最后一步,我们构造了一个匿名函数作为第二次PreOrderTraversal调用的Continuation,但是其内部直接调用了continuation参数——那么我们为什么不直接把它交给第二次调用呢?如下:
PreOrderTraversal(root.Left, left => PreOrderTraversal(root.Right, continuation));
我们使用Continuation实现了尾递归,其实是把原本应该分配在栈上的信息丢到了托管堆上。每个匿名方法其实都是托管堆上的对象,虽然说这种生存周期短的对象不会对内存资源方面造成多大问题,但是尽可能减少此类对象,对于性能肯定是有帮助的。这里再举一个更为明显的例子,求二叉树的大小(Size):
public static int GetSize(TreeNode root, Func<int, int> continuation) { if (root == null) return continuation(0); return GetSize(root.Left, leftSize => GetSize(root.Right, rightSize => continuation(leftSize + rightSize + 1) ) ); }
GetSize方法使用了Continuation,它的理解方法是“获取root的大小,再将结果传入continuation,并返回其调用结果”。我们可以将其进行改写,减少Continuation方法的构造次数:
public static int GetSize2(TreeNode root, int acc, Func<int, int> continuation) { if (root == null)
return continuation(acc);
return GetSize2(root.Left, acc, accLeftSize => GetSize2(root.Right, accLeftSize + 1, continuation)); }
GetSize2方法多了一个累加器参数,同时它的理解方式也有了变化:“将root的大小累加到acc上,再将结果传入continuation,并返回其调用结果”。也就是说GetSize2返回的其实是一个累加值,而并非是root参数的实际尺寸。当然,我们在调用时GetSize2时,只需将累加器置零便可:
GetSize2(root, 0, x => x)
小结
在命令式编程中,我们解决一些问题往往可以使用循环来代替递归,这样便不会因为数据规模造成堆栈溢出。但是在函数式编程中,要实现“循环”的唯一方法便是“递归”,因此尾递归和CPS对于函数式编程的意义非常重大。在函数式语言中,continuation的引入是非常自然的过程,实际上任何程序都可以通过所谓的CPS(Continuation Passing Style)变换而转换为使用continuation结构。了解尾递归,对于编程思维也有很大帮助,因此大家不妨多加思考和练习,让这样的方式为自己所用。





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· AI与.NET技术实操系列(二):开始使用ML.NET
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本