VINS（五）非线性优化与在线标定调整

首先根据最大后验估计（Maximum a posteriori estimation，MAP）构建非线性优化的目标函数。

初始化过程通过线性求解直接会给出一个状态的初值，而非线性优化的过程关键在于求解增量方程，并不断迭代到最优点，需要在初值以及后续的迭代点附近线性化（泰勒展开保留一阶后平方构建高斯牛顿梯度下降的增量方程）：

在初值x附近泰勒展开

$f(x+\Delta x) = f(x) + J\Delta x$

$costFunction = [f(x+\Delta x)]^{2}$

最小化costFunction的过程其实就是迭代求解增量方程

$H\Delta x = b$

其中$H = J^{T}J$，$b = -J^{T}f$

因此，首先需要定义状态的增量，主要因为旋转矩阵没有加法，无法迭代求解，因此在SO(3)流形的正切空间上定义四元数的加法，并表示成最小坐标的李代数（轴转角）形式

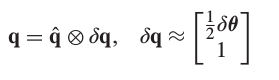
因此对应的error-state costFunction定义为：

注意该式求解的是迭代需要使用的增量，而不是初始化过程可以直接线性求解出的初值。这是优化过程和初始化过程中costFunction的主要不同点。 

接下来还需要建立对应的观测方程去计算residual及其Jacobian，并且推到误差的传播方程。和初始化过程中对比，增加的有：

• IMU中的旋转矩阵；
• 误差传播考虑旋转矩阵及其与translation之间的相关性；

对比初始化和非线性优化过程：

• 都是基于Sliding Window，但是初始化中每组Sliding Window只会计算一次，如果没有收敛到可以完成初始化，则扩大窗口大小，或者直接滑动窗口；
• Nonlinear Optimization中Sliding Window则是在固定的Sliding Window中求解增量方程迭代优化到满足一定条件（residual收敛或者限制固定迭代次数保证计算量的平衡）；