Ceres优化

　　Ceres Solver是谷歌2010就开始用于解决优化问题的C++库，2014年开源．在Google地图，Tango项目，以及著名的SLAM系统OKVIS和Cartographer的优化模块中均使用了Ceres Solver.

　　有关为何SLAM问题可以建模为最小二乘问题，进而使用最优化方法来求解，可以理解这一段话：

Maximum likelihood estimation (MLE) is a well-known estimation method used in many robotic and computer vision applications. Under Gaussian assumption, the MLE converts to a nonlinear least squares (NLS) problem. Efficient solutions to NLS exist and they are based on iteratively solving sparse linear systems until convergence.

　　在SLAM领域优化问题还可以使用g2o来求解．不过Ceres提供了自动求导功能，虽然是数值求导，但可以避免复杂的雅克比计算，目前来看Ceres相对于g2o的缺点仅仅是依赖的库多一些（g2o仅依赖Eigen）．但是提供了可以直接对数据进行操作的能力，相对于g2o应用在视觉SLAM中，更加倾向于通用的数值优化，最重要的是提供的官方资料比较全（看g2o简直受罪．．．）．详细的介绍可以参考google的文档：http://ceres-solver.org/features.html

　　优化问题的本质是调整优化变量，使得优化变量建模得出的估计值不断接近观测数据（使得目标函数下降），是最大似然框架下对优化变量的不断调整，得到优化变量建模得出的估计值在观测条件下的无偏估计过程．

　　这里已知的是固定的观测数据z，以及需要调整的初始估计值x₀．通常会建模成观测数据和估计值之间的最小二乘问题（但并不一定是最好的建模方式）:

　　 $\mathop{\arg\min}_{x_{i,j}} \ \ \frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{n}\left \|z_{i,j}-h(x{_{i,j}})) \right \| ^{2}$

一些概念：

ObjectiveFunction：目标函数；
ResidualBlock：残差（代价函数的二范数，有时不加区分），多个ResidualBlock组成完整的目标函数；
CostFunction：代价函数，观测数据与估计值的差，观测数据就是传感器获取的数据，估计值是使用别的方法获取（例如初始化，ICP，PnP或者匀速模型．．．）的从优化变量通过建模得出的观测值；例如从对极几何得到的相机位姿，三角化得到的地图点可以作为优化变量的初始值，但是需要利用坐标系变换和相机模型转化为2D平面上的像素坐标估计值，与实际测量得到的观测值之间构建最小二乘问题；
ParameterBlock：优化变量；
LossFunction：核函数，用来减小Outlier的影响，对应g2o中的edge->setRobustKernel()

求解步骤：

以寻找y=(10-x)^２的最小值为例

１．定义一个Functor(拟函数/函数对象)类，其中定义的是CostFunction. 需要重载函数调用运算符，从而可以像使用函数一样使用该类对象．（与普通函数相比，能够在类中存储状态，更加灵活）

　　operator()的形参，前面几个对应 problem.AddResidualBlock(cost_function, NULL, &x);中最后一部分优化变量，最后一个对应残差

struct CostFunctor {
   template <typename T>
   bool operator()(const T* const x, T* residual) const {
     residual[0] = T(10.0) - x[0];
     return true;
   }
};

这里模板参数T通常为double，在需要求residual的雅克比时，T=Jet

２．　建立非线性最小二乘问题，并使用Ceres Solver求解

int main(int argc, char** argv) {
  google::InitGoogleLogging(argv[0]);

  // The variable to solve for with its initial value.
  double initial_x = 5.0;
  double x = initial_x;

  // Build the problem.
  Problem problem;

  // Set up the only cost function (also known as residual). This uses
  // auto-differentiation to obtain the derivative (jacobian).
  CostFunction* cost_function =
      new AutoDiffCostFunction<CostFunctor, 1, 1>(new CostFunctor);
  problem.AddResidualBlock(cost_function, NULL, &x);

  // Run the solver!
  Solver::Options options;
  options.linear_solver_type = ceres::DENSE_QR;
  options.minimizer_progress_to_stdout = true;
  Solver::Summary summary;
  Solve(options, &problem, &summary);

  std::cout << summary.BriefReport() << "\n";
  std::cout << "x : " << initial_x
            << " -> " << x << "\n";
  return 0;
}

3. 参数选择

　　在做Bundle Adjustment过程中，建立好优化问题后，需要对优化求解器进行一些参数设置：

Solver::Options options;
options.gradient_tolerance = 1e-16;
options.function_tolerance = 1e-16;
...

梯度阈值　gradient_tolerance．
相邻两次迭代之间目标函数之差　function_tolerance．
梯度下降策略　trust_region_strategy　可选levenberg_marquardt，dogleg．
线性增量方程 HΔx=g 求解方法　linear_solver　可选sparse_schur，dense_schur，sparse_normal_cholesky，视觉SLAM中主要采用稀疏Schur Elimination/ Marginalization的方法（也就是消元法），将地图点的增量边缘化，先求出相机位姿的增量，可以极大地较少计算量，避免H矩阵直接求逆．
稀疏线性代数库　sparse_linear_algebra_library　可选suite_sparse，cx_sparse（ceres编译时需额外编译），cx_sparse相对suite_sparse，更精简速度较慢，但是不依赖BLAS和LAPACK．这个通常选择suite_sparse即可．
稠密线性代数库　dense_linear_algebra_library　可选eigen，lapack．
边缘化次序　ParameterBlockOrdering　设置那些优化变量在求解增量方程时优先被边缘化，一般会将较多的地图点先边缘化，不设置ceres会自动决定边缘化次序，这在SLAM里面常用于指定Sliding Window的范围．
多线程　这里的设置根据运行平台会有较大不同，对计算速度的影响也是最多的．分为计算雅克比时的线程数num_threads，以及求解线性增量方程时的线程数num_linear_solver_threads．
迭代次数　max_num_iterations，有时迭代多次均不能收敛，可能是初值不理想或者陷入了平坦的区域等等原因，需要设定一个最大迭代次数．

总结：

设置options细节较多，可以参考官方文档去设定：

　　http://ceres-solver.org/nnls_solving.html#solver-options．

通过实验发现除了多线程以及linear_solver_type，别的对优化性能和结果影响不是很大：

　　实验代码在：https://github.com/xushangnjlh/xushang_SLAM;

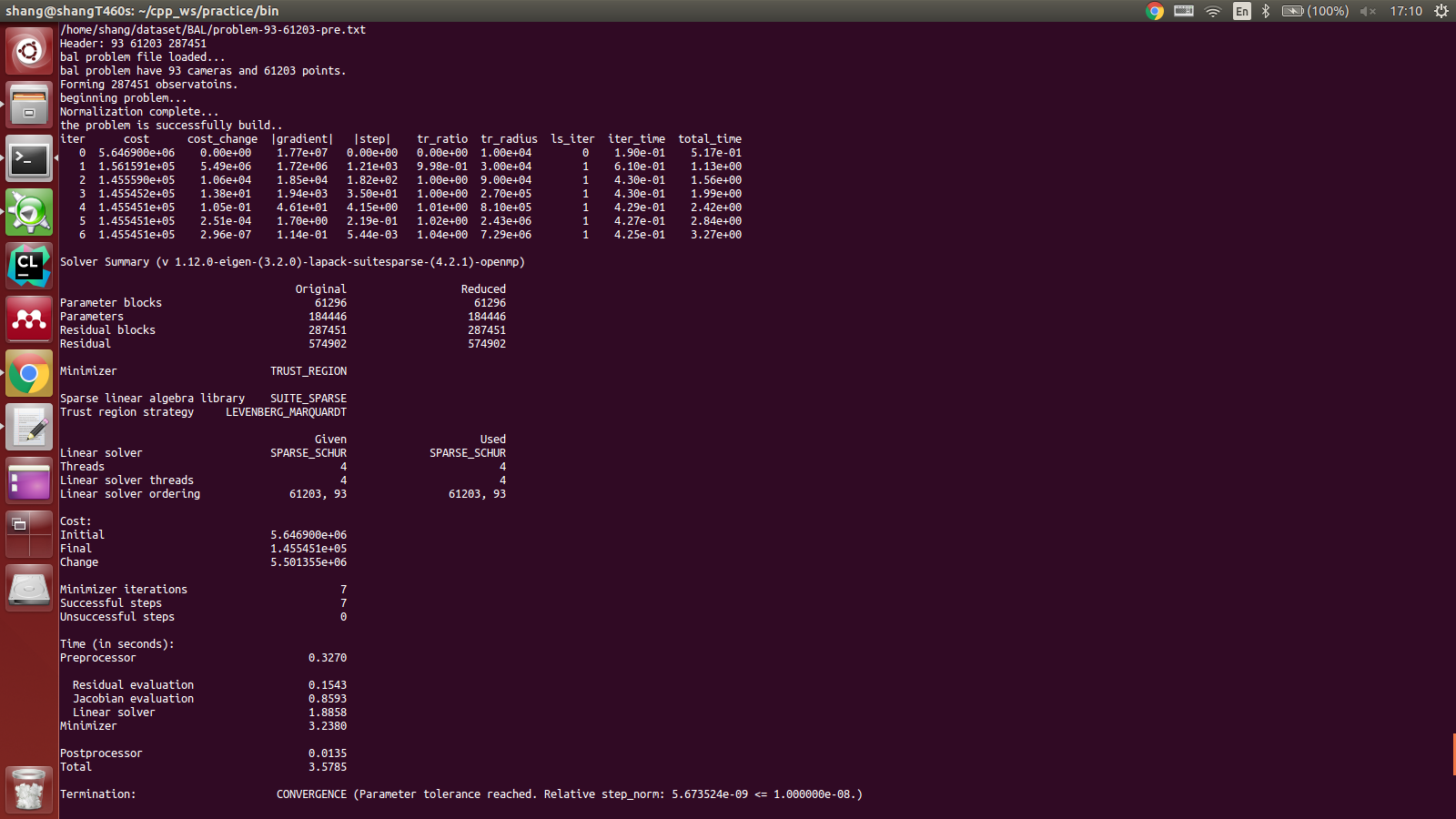
对于93个相机位姿 61203个地图点 287451个观测数据的SFM优化问题：

　　测试数据集http://grail.cs.washington.edu/projects/bal/final.html

边缘化的影响：

边缘化所有地图点Total Time: 3.6005s 其中Linear solver：1.8905s
边缘化2/3地图点Total Time: 5.4723s 其中Linear solver：3.7504s
边缘化1/3地图点Total Time: 7.0223s 其中Linear solver：5.3335s

线程影响（在四核CPU上测试）：

num_threads=1 Total Time：5.9113s
num_threads=2 Total Time：4.2645s
num_threads=4 Total Time：3.5785s
num_threads=8 Total Time：3.6472s

运行结果截图：

posted @ 2017-05-07 17:57 徐尚阅读(18358) 评论(2) 编辑收藏举报

刷新页面返回顶部

SLAM-BJTShang

Ceres优化

公告