西方有术傅里叶 (离散傅里叶变换的推导(1))

西方有术傅里叶

----离散傅里叶变换的推导(1)

首先让我们忘记严密的数学，忘记DFT，定性地思考一些东西。

DFT中涉及的一个就是相关，其实就是看两个信号的相似程度。越相似，相关系数就越大。如果没有用过相关，那一定用过加权平均，我们的成绩有时是会被加权平均的，数学英语权值大，不重要的科目权值小，这样平均来显示自己的实力是有些不公平，因为里面体现着老师对科目的偏好和重视，如果你的科目成绩分布恰巧和老师这个偏好和重视一致（相似），你的分数就高，这和相关其实是一个概念，只不过加权平均是归一化的，而相关可以归一化也可以不归一化。

其实DFT就是一个相关的过程，就是拿你的信号和不同频率的正弦余弦信号相关的过程。想想我们刚才说的相关和加权平均的概念，就不难理解了，不同频率的正余弦信号，就是老师心里的砝码（哪个科目重要，哪个科目不重要），你的信号就是你的成绩，需要放到老师提供的尺度下去衡量，越一致越相似你的分数就越高，只不过DFT比较公平，他考虑所有不同老师的标准，而不是一个。每个老师都有一个频率（即老师的标准），你得按照每个老师的标准去计算一遍，才能知道你在该老师标准下的成绩（即相关系数）。把每个老师的标准当成横坐标，把该标准下的成绩当成纵坐标，组成的图就是你信号的频谱了。

具体点就是，如上图所示，因为你成绩单上的课程不仅多，排列还毫无规律，为了能将你快速并顺利划分到合适的专业，需要对你的专业能力进行评定，所以将你成绩丢进各个系老师的标准中进行评定，评定结果表示，你在CS专业上能力突出，在文学领域还有待加强，为此马上可以得出将你划分入CS系中的概率比较大了。

既然已经文字化描述了下傅里叶变换的过程了，往下开始数学化点了。

先对刚刚提到的相关这个概念重新理解一下，理解傅里叶变换文中已经对信号相关性进行了详细了描述，现将其引动到这来。

信号的相关性(correlation)可以从噪声背景中检测出已知的信号，我们也可以利用这个方法检测信号波中是否含有某个频率的信号波：把一个待检测信号波乘以另一个信号波，得到一个新的信号波，再把这个新的信号波所有的点进行相加，从相加的结果就可以判断出这两个信号的相似程度。如下图：

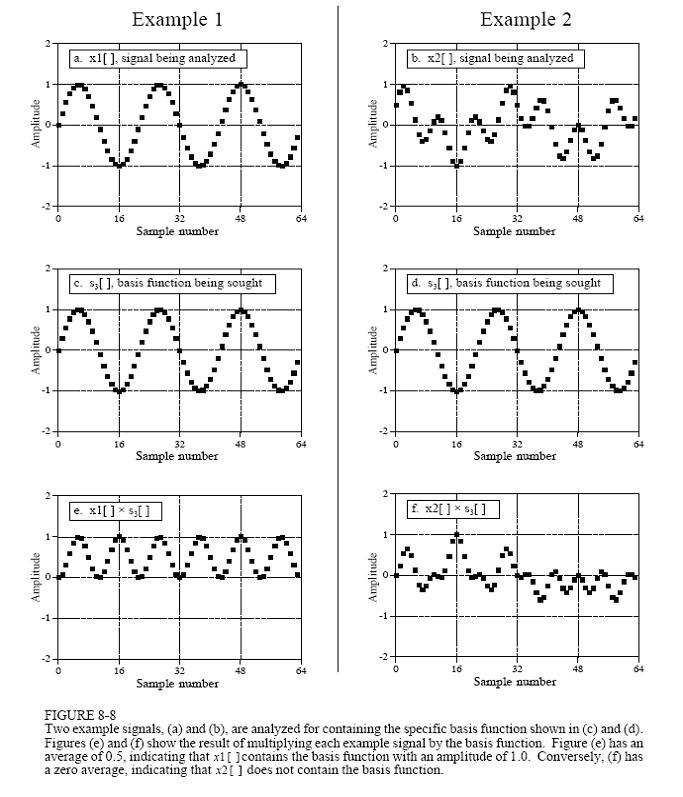
上面a和 b两个图是待检测信号波，图a很明显可以看出是个3个周期的正弦信号波，图b的信号波则看不出是否含有正弦或余弦信号，图c和d都是个3个周期的正弦信号波，图e和f分别是a、b两图跟c、d两图相乘后的结果，图e所有点的平均值是0.5，说明信号a含有振幅为1的正弦信号c，但图f所有点的平均值是0，则说明信号b不含有信号d。这个就是通过信号相关性来检测是否含有某个信号的方法。

先引用到这，到这边应该有个问题，为什么所有点的平均值是0.5时，便说明信号a含有振幅为1的正弦信号c ？

首先我们知道傅里叶级数的公式为：