[ZJOI2008] 树的统计Count
http://www.lydsy.com/JudgeOnline/problem.php?id=1036
终于调出来了
#include <iostream> #include <cstdio> #include <cstdlib> using namespace std; const int N = 3e4 + 10; #define gc getchar() #define lson jd << 1 #define rson (jd << 1) + 1 #define INF 1000000000 int n, m, now, Tree_clock; int ans_max, ans_sum; int head[N]; int tree[N], bef[N], deep[N], f[N], son[N], size[N], topp[N], data[N]; struct Node{ int v, nxt; }G[N * 2]; struct node{ int l, r; int w, max; }T[N << 2]; char how[10]; inline int read(){ int x = 0, f = 1; char c = gc; while(c < '0' || c > '9'){if(c == '-') f = -1; c = gc;} while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = gc; return x * f; } inline void add(int u, int v){ G[++ now].v = v; G[now].nxt = head[u]; head[u] = now; } void dfs_find_son(int u, int fa, int dep){ f[u] = fa; deep[u] = dep; size[u] = 1; for(int i = head[u]; ~ i; i = G[i].nxt){ int v = G[i].v; if(v == fa) continue ; dfs_find_son(v, u, dep + 1); size[u] += size[v]; if(!son[u] || size[son[u]] < size[v]) son[u] = v; } } void dfs_un_son(int u, int tp){ topp[u] = tp; tree[u] = ++ Tree_clock; bef[tree[u]] = u; if(!son[u]) return ; dfs_un_son(son[u], tp); for(int i = head[u]; ~ i; i = G[i].nxt){ int v = G[i].v; if(v != f[u] && v != son[u]) dfs_un_son(v, v); } } void build_tree(int l, int r, int jd){ T[jd].l = l; T[jd].r = r; if(l == r){ T[jd].w = T[jd].max = data[bef[l]]; return ; } int mid = (l + r) >> 1; build_tree(l, mid, lson); build_tree(mid + 1, r, rson); T[jd].max = max(T[lson].max, T[rson].max); T[jd].w = T[lson].w + T[rson].w; } void Sec_G(int l, int r, int jd, int x, int yj){ if(l == r){ T[jd].w += yj; T[jd].max += yj; return ; } int mid = (l + r) >> 1; if(x <= mid) Sec_G(l, mid, lson, x, yj); else Sec_G(mid + 1, r, rson, x, yj); T[jd].max = max(T[lson].max, T[rson].max); T[jd].w = T[lson].w + T[rson].w; } void ask_max(int l, int r, int jd, int x, int y){ if(x <= l && r <= y){ ans_max = max(ans_max, T[jd].max); return ; } int mid = (l + r) >> 1; if(x <= mid) ask_max(l, mid, lson, x, y); if(y > mid) ask_max(mid + 1, r, rson, x, y); T[jd].max = max(T[lson].max, T[rson].max); T[jd].w = T[lson].w + T[rson].w; } void ask_sum(int l, int r, int jd, int x, int y){ if(x <= l && r <= y){ ans_sum += T[jd].w; return ; } int mid = (l + r) >> 1; if(x <= mid) ask_sum(l, mid, lson, x, y); if(y > mid) ask_sum(mid + 1, r, rson, x, y); T[jd].max = max(T[lson].max, T[rson].max); T[jd].w = T[lson].w + T[rson].w; } int find_max(int x, int y){ int tp1 = topp[x], tp2 = topp[y]; int ans = - INF; while(tp1 != tp2){ if(deep[tp1] < deep[tp2]) swap(x, y), swap(tp1, tp2); ans_max = - INF; ask_max(1, n, 1, tree[tp1], tree[x]); ans = max(ans, ans_max); x = f[tp1]; tp1 = topp[x]; } ans_max = - INF; deep[x] > deep[y] ? ask_max(1, n, 1, tree[y], tree[x]) : ask_max(1, n, 1, tree[x], tree[y]); ans = max(ans, ans_max); return ans; } int find_sum(int x, int y){ int tp1 = topp[x], tp2 = topp[y]; int ans = 0; while(tp1 != tp2){ if(deep[tp1] < deep[tp2]) swap(x, y), swap(tp1, tp2); ans_sum = 0; ask_sum(1, n, 1, tree[tp1], tree[x]); ans += ans_sum; x = f[tp1]; tp1 = topp[x]; } ans_sum = 0; deep[x] > deep[y] ? ask_sum(1, n, 1, tree[y], tree[x]) : ask_sum(1, n, 1, tree[x], tree[y]); ans += ans_sum; return ans; } int main() { n = read(); for(int i = 0; i <= n; i ++) head[i] = -1; for(int i = 1; i < n; i ++){ int u, v; u = read(); v = read(); add(u, v); add(v, u); } for(int i = 1; i <= n; i ++) data[i] = read(); dfs_find_son(1, 0, 1); dfs_un_son(1, 1); build_tree(1, n, 1); m = read(); while(m --){ int x, y; scanf("%s", how); x = read(); y = read(); if(how[0] == 'C'){ Sec_G(1, n, 1, tree[x], y - data[x]); data[x] = y; } else if(how[1] == 'M') printf("%d\n", find_max(x, y)); else printf("%d\n", find_sum(x, y)); } return 0; } /* */
加深一下理解
(树剖--将树转化成链,用数据结构维护转化成的链)-- <代码长度与思维难度不成正比的算法>
树剖的代码还是不难理解的
首先给出一棵树
(上面的例题)
输入的第一行为一个整数n,表示节点的个数。接下来n – 1行,每行2个整数a和b,表示节点a和节点b之间有
一条边相连。接下来n行,每行一个整数,第i行的整数wi表示节点i的权值。接下来1行,为一个整数q,表示操作
的总数。接下来q行,每行一个操作,以“CHANGE u t”或者“QMAX u v”或者“QSUM u v”的形式给出。
对于100%的数据,保证1<=n<=30000,0<=q<=200000;中途操作中保证每个节点的权值w在-30000到30000之间。

12 1 2 1 3 1 4 2 6 2 5 6 11 6 12 3 7 4 8 4 9 4 10 9 13 13 14 1 2 3 4 5 6 7 8 9 10 11 12 13 14
在树上进行许多操作,这道题
将树上的某点的权值进行变化,求树上两点间的权值的和
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。
树链剖分就是见树上的所有点(或边)按照某种顺序存入一种数据结构,(这里用线段树),这样就转换成了一条链上的问题
当然,关于这个它有两个重要的性质:
(1)轻边(u,v)中,size(v)<=size(u/2)
(2)从根到某一点的路径上,不超过logn条轻边和不超过logn条重路径。
如果是两次dfs,那么第一次dfs就是找重边,也就是记录下所有的重边。
然后第二次dfs就是连接重边形成重链,具体过程就是:以根节点为起点,沿着重边向下拓展,拉成重链,不在当前重链上的节
点,都以该节点为起点向下重新拉一条重链。(这个比较好理解)
几个概念:
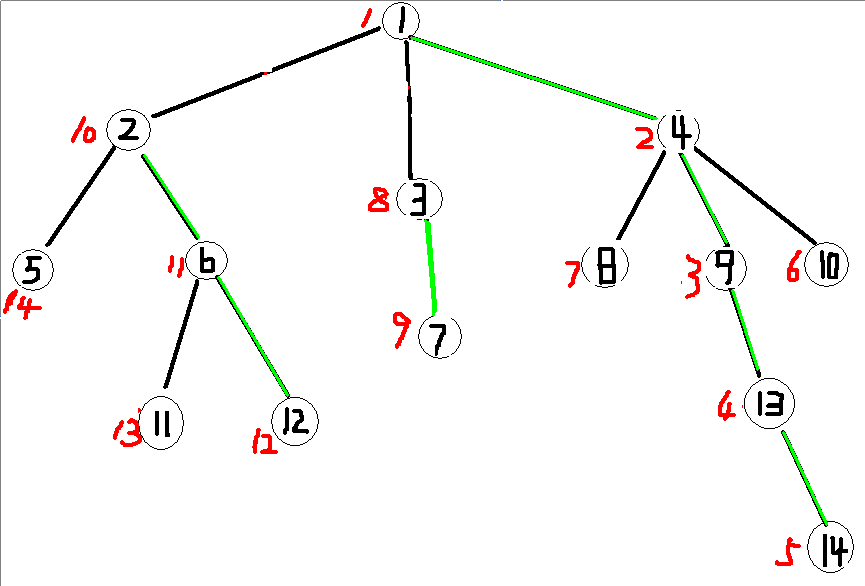
重儿子:一个节点的儿子中儿子最多的节点(下图绿色的边为重边,重边的点就是重儿子<貌似不严谨>)
重边:up(图中绿色的边)
重链:几条重边相连
然而这种顺序是重要的,不然会起副作用的
顺序就是:从根dfs先遍历重儿子的顺序
下图每个节点在树中的编号分比为:1-10-8-2-14-11-9-7-3-6-13-12-4-5 (节点旁边的红色数字)
可以发现一条重链上的点在线段树中的编号是相连的,由此可以想到当处理一种操作时,每遇到一条链(图中绿色的边相连构成的),我们就可以
整体操作,这样就可以大大提高效率
比如当查询连接12-14节点的路径上点的编号的最大值
当遇到14节点时,我们可以先查询1-14号节点的最大值,因为1-14号节点之间的点的编号一定是相连的,所以这里相当于
线段树的区间查询操作,查询线段树区间1-14的最大值,复杂度是log级别。
那如何记录1号节点和14号节点之间的关系呢??
先看定义的几个变量
size[i] 表示i号节点的儿子数量,也就是i号节点的重量
son[i] 记录i号节点的重儿子
deep[i] 表示i号节点的深度
top[i] 记录i号节点所在的链的深度最小的节点是谁,这样就可以解决确定1号节点和14号节点之间关系的问题top[14] = 1;
f[i] 表示i号节点的父亲是谁
说到这里,接着上面的例子,之前求出了1-14这条链上的最大值,接下来我们令x(当前节点,在上面的例子中就是14号)= f[top[x]]
就是令当前节点为当前节点所在的链的头节点(深度最小)的父亲,然后继续跳
注意,当我们每次要求两个节点之间路径上的最大值时,向上跳的总要是深度更大的那个
像上面的例子,我们先在两个点分别跳到了12和0,这个0是因为当14号变为当前节点所在的链的头节点(深度最小)的父亲时
成了0,那么接下来只有12号节点去跳,当12号节点也跳到0号节点时,我们就求出了answer
那么解决这个问题的过程就是
当两点不在一条重链上时,我们分开跳,当在一条重链上时,只需一次线段树去检查询
求两点间的权值的和与求最大值是一样的
方便理解这个图的节点编号和权值是相等的。
树剖还有操作呢。。。。


