分治算法
一、分治
1、定义:分治,也就是分而治之。
它的一般步骤是:
① 将原问题分解成若干个规模较小的子问题(子问题和原问题的结构一样,只是规模不一样)
② 子问题又不断分解成规模更小的子问题,直到不能再分解(直到可以轻易计算出子问题的解)
③ 利用子问题的解推导出原问题的解
分治策略非常适合用递归
需要注意的是:子问题之间是相互独立的
2、分治的应用
- 快速排序
- 归并排序
- Karatsuba算法(大数乘法)
3、分治时间复杂度的计算--主定理

4、最大连续子序列和
子序列:按照原序列的排序顺序,从原序列取出部分元素
连续子序列:按照原序列的排序顺序,连续地从原序列取出部分元素
-
举例:
原序列:–2、1、–3、4、–1、2、1、–5、4
子序列可以是:–2、1、1、4 还可以是:4、1、4 还可以是:2、1、–5、4 等等
连续子序列可以是:–2、1、–3、4、–1 还可以是:–3、4、–1 还可以是:2、1、–5、4 等等
子串、子数组、子区间必须是连续的,子序列是可以不连续的
解法:分治
◼ 将序列均匀地分割成 2 个子序列
- [begin , end) = [begin , mid) + [mid , end),mid = (begin + end) >> 1
◼ 假设 [begin , end) 的最大连续子序列和是 S[i , j) ,那么它有 3 种可能
- [i , j) 存在于 [begin , mid) 中,同时 S[i , j) 也是 [begin , mid) 的最大连续子序列和
- [i , j) 存在于 [mid , end) 中,同时 S[i , j) 也是 [mid , end) 的最大连续子序列和
- [i , j) 一部分存在于 [begin , mid) 中,另一部分存在于 [mid , end) 中
- [i , j) = [i , mid) + [mid , j)
- S[i , mid) = max { S[k , mid) },begin ≤ k < mid
- S[mid , j) = max { S[mid , k) },mid < k ≤ end
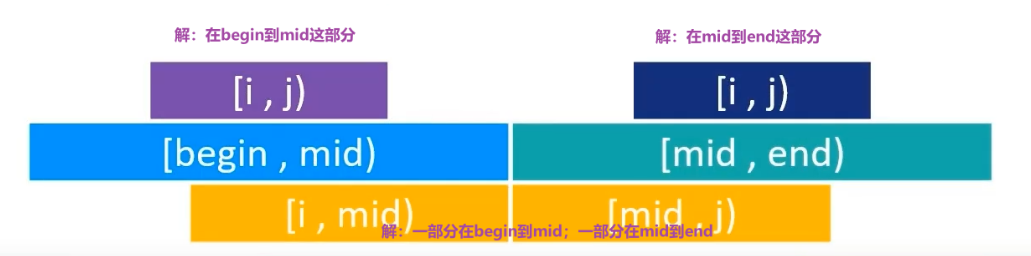
对于解:只在左边或者只在右边,可以直接使用 递归
对于解:在中间,一部分在左边,一部分在右边的情况:
- 需要先 从中间mid开始统计[mid - 1, 左边某个元素] 统计出左边的最大值
- 再从中间mid开始统计[mid, 右边某个元素] 统计出右边的最大值
- 然后左边最大值+右边最大值,就是 横跨两个区域的解
static int maxSubArray(int[] nums) {
if(nums == null || nums.length == 0) return 0;
return maxSubArray(nums, 0, nums.length);
}
/**
* 分治法
*/
private static int maxSubArray(int[] nums, int begin, int end) {
if(end - begin < 2) return nums[begin];
int mid = (begin + end) >> 1;
// 要从中间mid开始统计[mid - 1, 左边某个元素]、[mid, 右边某个元素]的连续最大子序列和
int leftMax = nums[mid - 1];
int leftSum = leftMax;
for(int i = mid - 2; i >= begin; i--) {
leftSum += nums[i];
leftMax = Math.max(leftMax, leftSum);
}
int rightMax = nums[mid];
int rightSum = rightMax;
for(int i = mid + 1; i < end; i++) {
rightSum += nums[i];
rightMax = Math.max(rightMax, rightSum);
}
int midMax = leftMax + rightMax;
return Math.max(midMax, //中间的最大连续子序列和
Math.max(maxSubArray(nums, begin, mid -1), maxSubArray(nums,mid, end))); //左边、右边的最大连续子序列和
}
如果本文对你有帮助的话记得给一乐点个赞哦,感谢!
本文来自博客园,作者:一乐乐,转载请注明原文链接:https://www.cnblogs.com/shan333/p/16602068.html




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 我干了两个月的大项目,开源了!
· 推荐一款非常好用的在线 SSH 管理工具
· 千万级的大表,如何做性能调优?
· 聊一聊 操作系统蓝屏 c0000102 的故障分析
· .NET周刊【1月第1期 2025-01-05】