算法基础~链表~链表求环解法二，快慢指针法【数学思路】

算法基础~链表~链表求环解法二，快慢指针法【数学思路】

1，链表成环图解

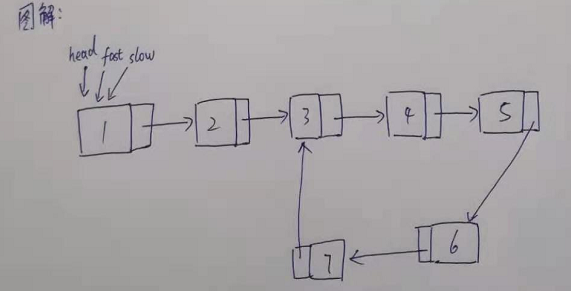
2，常识：两个速度不一的物体在环形跑道一定可以相遇。

3,先假设快的物体速度是慢的物体的两倍。

过程：一开始 fast=slow=head； 快慢指针都在 1 这个结点上

第一次移动：fast->3, slow->2;

第二次移动：fast->5, slow->3;

第三次移动：fast->7, slow->4;

第四次移动：fast->4, slow->5;

第五次移动：fast->6, slow->6;         ~则 6 这个结点就是相遇点。

 

4，过程分析后的图解【链表起点、环起点、相遇点】

 

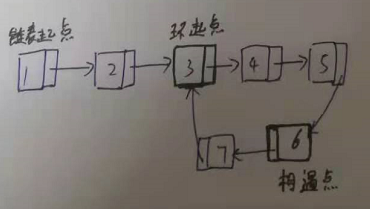
 5，这题解法~数学解法~假设+图解推导法

设：链表起点到环起点距离是a，环起点到相遇点距离是b，相遇点到环起点距离是c，

还有一开始设：“快指针速度是慢指针速度的两倍”---》快指针移动的距离 = 2 * 慢指针移动距离的；即 a + b+ c +b = 2 （a + b）;

---> a = c;

得出结论：【链表起点到环起点距离 = 相遇点到环起点距离】--》距离相等 --》等长，则一起同步循环遍历，且交点便是“环起点”啦。

 

6，直接上代码，分析过程如上：

class Solution{
    public:
    ListNode *detectCycle(ListNode *head){
        ListNode *fast = head;
        ListNode *slow = head;
        ListNode *meet = NULL;
        while(fast){
            fast = fast->next;
            slow = slow->next;
            if(!fast){    //如果fast到达链尾，则返回NULL
                return NULL；
            }
            fast = fast->next;
            //找到相遇点
            if(fast == slow){
                meet = fast;
            }
        }
        //等长，同步遍历，直到遍历到“环起点”
        while(head && fast){
            if(head == fast){
                return head;
            }
            head = head->next;
            fast = fast-=>next;
        }
        return NULL;
    
    }
}