Java数据结构和算法(二):数组
上篇博客我们简单介绍了数据结构和算法的概念,对此模糊很正常,后面会慢慢通过具体的实例来介绍。本篇博客我们介绍数据结构的鼻祖——数组,可以说数组几乎能表示一切的数据结构,在每一门编程语言中,数组都是重要的数据结构,当然每种语言对数组的实现和处理也不相同,但是本质是都是用来存放数据的的结构,这里我们以Java语言为例,来详细介绍Java语言中数组的用法。
1、Java数组介绍
在Java中,数组是用来存放同一种数据类型的集合,注意只能存放同一种数据类型(Object类型数组除外)。
①、数组的声明
第一种方式:
|
1
|
数据类型 [] 数组名称 = new 数据类型[数组长度]; |
这里 [] 可以放在数组名称的前面,也可以放在数组名称的后面,我们推荐放在数组名称的前面,这样看上去 数据类型 [] 表示的很明显是一个数组类型,而放在数组名称后面,则不是那么直观。
第二种方式:
|
1
|
数据类型 [] 数组名称 = {数组元素1,数组元素2,......} |
这种方式声明数组的同时直接给定了数组的元素,数组的大小由给定的数组元素个数决定。
|
1
2
3
4
|
//声明数组1,声明一个长度为3,只能存放int类型的数据int [] myArray = new int[3];//声明数组2,声明一个数组元素为 1,2,3的int类型数组int [] myArray2 = {1,2,3}; |
②、访问数组元素以及给数组元素赋值
数组是存在下标索引的,通过下标可以获取指定位置的元素,数组小标是从0开始的,也就是说下标0对应的就是数组中第1个元素,可以很方便的对数组中的元素进行存取操作。
前面数组的声明第二种方式,我们在声明数组的同时,也进行了初始化赋值。
|
1
2
3
4
5
6
|
//声明数组,声明一个长度为3,只能存放int类型的数据int [] myArray = new int[3];//给myArray第一个元素赋值1myArray[0] = 1;//访问myArray的第一个元素System.out.println(myArray[0]); |
上面的myArray 数组,我们只能赋值三个元素,也就是下标从0到2,如果你访问 myArray[3] ,那么会报数组下标越界异常。
③、数组遍历
数组有个 length 属性,是记录数组的长度的,我们可以利用length属性来遍历数组。
|
1
2
3
4
5
|
//声明数组2,声明一个数组元素为 1,2,3的int类型数组int [] myArray2 = {1,2,3};for(int i = 0 ; i < myArray2.length ; i++){ System.out.println(myArray2[i]);} |
2、用类封装数组实现数据结构
上一篇博客我们介绍了一个数据结构必须具有以下基本功能:
①、如何插入一条新的数据项
②、如何寻找某一特定的数据项
③、如何删除某一特定的数据项
④、如何迭代的访问各个数据项,以便进行显示或其他操作
而我们知道了数组的简单用法,现在用类的思想封装一个数组,实现上面的四个基本功能:
ps:假设操作人是不会添加重复元素的,这里没有考虑重复元素,如果添加重复元素了,后面的查找,删除,修改等操作只会对第一次出现的元素有效。
1 package com.ys.array;
2
3 public class MyArray {
4 //定义一个数组
5 private int [] intArray;
6 //定义数组的实际有效长度
7 private int elems;
8 //定义数组的最大长度
9 private int length;
10
11 //默认构造一个长度为50的数组
12 public MyArray(){
13 elems = 0;
14 length = 50;
15 intArray = new int[length];
16 }
17 //构造函数,初始化一个长度为length 的数组
18 public MyArray(int length){
19 elems = 0;
20 this.length = length;
21 intArray = new int[length];
22 }
23
24 //获取数组的有效长度
25 public int getSize(){
26 return elems;
27 }
28
29 /**
30 * 遍历显示元素
31 */
32 public void display(){
33 for(int i = 0 ; i < elems ; i++){
34 System.out.print(intArray[i]+" ");
35 }
36 System.out.println();
37 }
38
39 /**
40 * 添加元素
41 * @param value,假设操作人是不会添加重复元素的,如果有重复元素对于后面的操作都会有影响。
42 * @return添加成功返回true,添加的元素超过范围了返回false
43 */
44 public boolean add(int value){
45 if(elems == length){
46 return false;
47 }else{
48 intArray[elems] = value;
49 elems++;
50 }
51 return true;
52 }
53
54 /**
55 * 根据下标获取元素
56 * @param i
57 * @return查找下标值在数组下标有效范围内,返回下标所表示的元素
58 * 查找下标超出数组下标有效值,提示访问下标越界
59 */
60 public int get(int i){
61 if(i<0 || i>elems){
62 System.out.println("访问下标越界");
63 }
64 return intArray[i];
65 }
66 /**
67 * 查找元素
68 * @param searchValue
69 * @return查找的元素如果存在则返回下标值,如果不存在,返回 -1
70 */
71 public int find(int searchValue){
72 int i ;
73 for(i = 0 ; i < elems ;i++){
74 if(intArray[i] == searchValue){
75 break;
76 }
77 }
78 if(i == elems){
79 return -1;
80 }
81 return i;
82 }
83 /**
84 * 删除元素
85 * @param value
86 * @return如果要删除的值不存在,直接返回 false;否则返回true,删除成功
87 */
88 public boolean delete(int value){
89 int k = find(value);
90 if(k == -1){
91 return false;
92 }else{
93 if(k == elems-1){
94 elems--;
95 }else{
96 for(int i = k; i< elems-1 ; i++){
97 intArray[i] = intArray[i+1];
98
99 }
100 elems--;
101 }
102 return true;
103 }
104 }
105 /**
106 * 修改数据
107 * @param oldValue原值
108 * @param newValue新值
109 * @return修改成功返回true,修改失败返回false
110 */
111 public boolean modify(int oldValue,int newValue){
112 int i = find(oldValue);
113 if(i == -1){
114 System.out.println("需要修改的数据不存在");
115 return false;
116 }else{
117 intArray[i] = newValue;
118 return true;
119 }
120 }
121
122 }
测试:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
package com.ys.test;import com.ys.array.MyArray;public class MyArrayTest { public static void main(String[] args) { //创建自定义封装数组结构,数组大小为4 MyArray array = new MyArray(4); //添加4个元素分别是1,2,3,4 array.add(1); array.add(2); array.add(3); array.add(4); //显示数组元素 array.display(); //根据下标为0的元素 int i = array.get(0); System.out.println(i); //删除4的元素 array.delete(4); //将元素3修改为33 array.modify(3, 33); array.display(); }} |
打印结果为:
3、分析数组的局限性
通过上面的代码,我们发现数组是能完成一个数据结构所有的功能的,而且实现起来也不难,那数据既然能完成所有的工作,我们实际应用中为啥不用它来进行所有的数据存储呢?那肯定是有原因呢。
数组的局限性分析:
①、插入快,对于无序数组,上面我们实现的数组就是无序的,即元素没有按照从大到小或者某个特定的顺序排列,只是按照插入的顺序排列。无序数组增加一个元素很简单,只需要在数组末尾添加元素即可,但是有序数组却不一定了,它需要在指定的位置插入。
②、查找慢,当然如果根据下标来查找是很快的。但是通常我们都是根据元素值来查找,给定一个元素值,对于无序数组,我们需要从数组第一个元素开始遍历,直到找到那个元素。有序数组通过特定的算法查找的速度会比无需数组快,后面我们会讲各种排序算法。
③、删除慢,根据元素值删除,我们要先找到该元素所处的位置,然后将元素后面的值整体向前面移动一个位置。也需要比较多的时间。
④、数组一旦创建后,大小就固定了,不能动态扩展数组的元素个数。如果初始化你给一个很大的数组大小,那会白白浪费内存空间,如果给小了,后面数据个数增加了又添加不进去了。
很显然,数组虽然插入快,但是查找和删除都比较慢,而且扩展性差,所以我们一般不会用数组来存储数据,那有没有什么数据结构插入、查找、删除都很快,而且还能动态扩展存储个数大小呢,答案是有的,但是这是建立在很复杂的算法基础上,后面我们也会详细讲解。
4、分析数组在内存中的存储
我们知道Java里当一个对象使用关键字“new”创建时,会在堆上分配内存空间,然后返回对象的引用,这对数组来说也是一样的,因为数组也是一个对象。
新建一个数组
int[] arr = new int[4];
上面这段代码可以看成两部分,一部分是数组引用,即在代码中定义的数组引用变量;另一部分是实际的数组对象,这部分是在堆内存里运行的,通常无法直接访问,只能通过数组引用变量来访问。
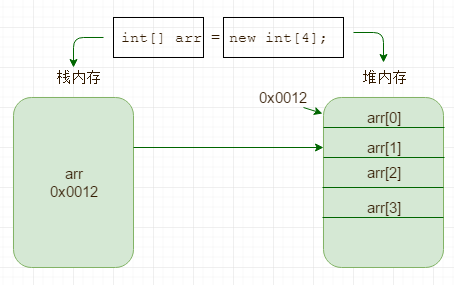
栈内存中存储所定义并初始化的引用变量arr,堆内存中存储arr指向的4个数组arr[0],arr[1],arr[2],arr[3]
5、扩展
1)滑动窗口练习题
有一个整型数组 arr 和一个大小为 w 的窗口从数组的最左边滑到最右边,窗口每次向右边滑一个位置。 返回一个长度为n-w+1的数组res,res[i]表示每一种窗口状态下的最大值。 以数组为[4,3,5,4,3,3,6,7],w=3为例。因为第一个窗口[4,3,5]的最大值为5,第二个窗口[3,5,4]的最大值为5,第三个窗口[5,4,3]的最大值为5。第四个窗口[4,3,3]的最大值为4。第五个窗口[3,3,6]的最大值为6。第六个窗口[3,6,7]的最大值为7。所以最终返回[5,5,5,4,6,7]。
给定整形数组arr及它的大小n,同时给定w,请返回res数组。保证w小于等于n,同时保证数组大小小于等于500。
[4,3,5,4,3,3,6,7],8,3
返回:[5,5,5,4,6,7]
import java.util.*; public class SlideWindow { public int[] slide(int[] arr, int n, int w) { //result数组中保存每个窗口状态下的最大值 int[] result = new int[n-w+1]; //记录双端队列队头的下标 ,队尾下标 int[] qmax = new int[n]; int front = 0, back = 0; //j 标记是否达到窗口大小,同时记录result中下一个应该放入的元素的下标 int j = 0; for(int i=0; i<n; i++){ while(front < back && arr[qmax[back-1]] < arr[i])//back为当前要往qmax中放入的值 back--; qmax[back++] = i; if(j+w-1 == i){ //达到窗口长度 result[j] = arr[qmax[front]]; j++; } if(qmax[front]+w-1 == i){ //队头过期 front++; } } return result; } }
2)数组变树练习题
对于一个没有重复元素的整数数组,请用其中元素构造一棵MaxTree,MaxTree定义为一棵二叉树,其中的节点与数组元素一一对应,同时对于MaxTree的每棵子树,它的根的元素值为子树的最大值。现有一建树方法,对于数组中的每个元素,其在树中的父亲为数组中它左边比它大的第一个数和右边比它大的第一个数中更小的一个。若两边都不存在比它大的数,那么它就是树根。请设计O(n)的算法实现这个方法。
给定一个无重复元素的数组A和它的大小n,请返回一个数组,其中每个元素为原数组中对应位置元素在树中的父亲节点的编号,若为根则值为-1。
测试样例:
[3,1,4,2],4
返回:[2,0,-1,2]
思路:要求时间复杂度为O(n),题目中已经有提示了,其实和最大最小堆有一点相似,对于大顶堆,我们常用树的方式理解,但是实际上可以用线性表存储(即数组),因此它需要是一棵完全二叉树(中间不能缺节点)。本题中的MaxTree只要求是二叉树就行了~,限制少一些,所以构建的时间复杂度也比建立大顶堆低一些。(大根堆构建初堆的时间复杂度也是O(n)) 利用栈可以快速找出左边和右边第一个比它大的值。



