Java数据结构和算法(三):常用排序算法与经典题型
常用的八种排序算法
1.直接插入排序
我们经常会到这样一类排序问题:把新的数据插入到已经排好的数据列中。将第一个数和第二个数排序,然后构成一个有序序列将第三个数插入进去,构成一个新的有序序列。对第四个数、第五个数……直到最后一个数,重复第二步。如题所示:

直接插入排序(Straight Insertion Sorting)的基本思想:在要排序的一组数中,假设前面(n-1) [n>=2] 个数已经是排好顺序的,现在要把第n个数插到前面的有序数中,使得这n个数也是排好顺序的。如此反复循环,直到全部排好顺序。
代码实现:
首先设定插入次数,即循环次数,for(int i=1;i<length;i++),1个数的那次不用插入。
设定插入数和得到已经排好序列的最后一个数的位数。insertNum和j=i-1。
从最后一个数开始向前循环,如果插入数小于当前数,就将当前数向后移动一位。
将当前数放置到空着的位置,即j+1。
代码如下:
public void insertSort(int [] a){ int len=a.length;//单独把数组长度拿出来,提高效率 int insertNum;//要插入的数 for(int i=1;i<len;i++){//因为第一次不用,所以从1开始 insertNum=a[i]; int j=i-1;//序列元素个数 while(j>=0&&a[j]>insertNum){//从后往前循环,将大于insertNum的数向后移动 a[j+1]=a[j];//元素向后移动 j--; } a[j+1]=insertNum;//找到位置,插入当前元素 } }
2.希尔排序
针对直接插入排序的下效率问题,有人对次进行了改进与升级,这就是现在的希尔排序。希尔排序,也称递减增量排序算法,是插入排序的一种更高效的改进版本。希尔排序是非稳定排序算法。
希尔排序是基于插入排序的以下两点性质而提出改进方法的:
- 插入排序在对几乎已经排好序的数据操作时, 效率高, 即可以达到线性排序的效率
- 但插入排序一般来说是低效的, 因为插入排序每次只能将数据移动一位
如图所示:

对于直接插入排序问题,数据量巨大时。
将数的个数设为n,取奇数k=n/2,将下标差值为k的数分为一组,构成有序序列。
再取k=k/2 ,将下标差值为k的书分为一组,构成有序序列。
重复第二步,直到k=1执行简单插入排序。
代码实现:
首先确定分的组数。
然后对组中元素进行插入排序。
然后将length/2,重复1,2步,直到length=0为止。
public void sheelSort(int [] a){ int len=a.length;//单独把数组长度拿出来,提高效率 while(len!=0){ len=len/2; for(int i=0;i<len;i++){//分组 for(int j=i+len;j<a.length;j+=len){//元素从第二个开始 int k=j-len;//k为有序序列最后一位的位数 int temp=a[j];//要插入的元素 /*for(;k>=0&&temp<a[k];k-=len){ a[k+len]=a[k]; }*/ while(k>=0&&temp<a[k]){//从后往前遍历 a[k+len]=a[k]; k-=len;//向后移动len位 } a[k+len]=temp; } } } }
3.简单选择排序
常用于取序列中最大最小的几个数时。
(如果每次比较都交换,那么就是交换排序;如果每次比较完一个循环再交换,就是简单选择排序。)
遍历整个序列,将最小的数放在最前面。
遍历剩下的序列,将最小的数放在最前面。
重复第二步,直到只剩下一个数。

代码实现:
首先确定循环次数,并且记住当前数字和当前位置。
将当前位置后面所有的数与当前数字进行对比,小数赋值给key,并记住小数的位置。
比对完成后,将最小的值与第一个数的值交换。
重复2、3步。
public void selectSort(int[]a){ int len=a.length; for(int i=0;i<len;i++){//循环次数 int value=a[i]; int position=i; for(int j=i+1;j<len;j++){//找到最小的值和位置 if(a[j]<value){ value=a[j]; position=j; } } a[position]=a[i];//进行交换 a[i]=value; } }
4.堆排序
对简单选择排序的优化。
将序列构建成大顶堆。
将根节点与最后一个节点交换,然后断开最后一个节点。
重复第一、二步,直到所有节点断开。

代码如下:
public void heapSort(int[] a){ int len=a.length; //循环建堆 for(int i=0;i<len-1;i++){ //建堆 buildMaxHeap(a,len-1-i); //交换堆顶和最后一个元素 swap(a,0,len-1-i); } } //交换方法 private void swap(int[] data, int i, int j) { int tmp=data[i]; data[i]=data[j]; data[j]=tmp; } //对data数组从0到lastIndex建大顶堆 private void buildMaxHeap(int[] data, int lastIndex) { //从lastIndex处节点(最后一个节点)的父节点开始 for(int i=(lastIndex-1)/2;i>=0;i--){ //k保存正在判断的节点 int k=i; //如果当前k节点的子节点存在 while(k*2+1<=lastIndex){ //k节点的左子节点的索引 int biggerIndex=2*k+1; //如果biggerIndex小于lastIndex,即biggerIndex+1代表的k节点的右子节点存在 if(biggerIndex<lastIndex){ //若果右子节点的值较大 if(data[biggerIndex]<data[biggerIndex+1]){ //biggerIndex总是记录较大子节点的索引 biggerIndex++; } } //如果k节点的值小于其较大的子节点的值 if(data[k]<data[biggerIndex]){ //交换他们 swap(data,k,biggerIndex); //将biggerIndex赋予k,开始while循环的下一次循环,重新保证k节点的值大于其左右子节点的值 k=biggerIndex; }else{ break; } } } }
5.冒泡排序
很简单,用到的很少,据了解,面试的时候问的比较多!
将序列中所有元素两两比较,将最大的放在最后面。
将剩余序列中所有元素两两比较,将最大的放在最后面。
重复第二步,直到只剩下一个数。

代码实现:
设置循环次数。
设置开始比较的位数,和结束的位数。
两两比较,将最小的放到前面去。
重复2、3步,直到循环次数完毕。
public void bubbleSort(int []a){ int len=a.length; for(int i=0;i<len;i++){ for(int j=0;j<len-i-1;j++){//注意第二重循环的条件 if(a[j]>a[j+1]){ int temp=a[j]; a[j]=a[j+1]; a[j+1]=temp; } } } }
6.快速排序
要求时间最快时。
选择第一个数为p,小于p的数放在左边,大于p的数放在右边。
递归的将p左边和右边的数都按照第一步进行,直到不能递归。

public void quickSort(int[]a,int start,int end){ if(start<end){ int baseNum=a[start];//选基准值 int midNum;//记录中间值 int i=start; int j=end; do{ while((a[i]<baseNum)&&i<end){ i++; } while((a[j]>baseNum)&&j>start){ j--; } if(i<=j){ midNum=a[i]; a[i]=a[j]; a[j]=midNum; i++; j--; } }while(i<=j); if(start<j){ quickSort(a,start,j); } if(end>i){ quickSort(a,i,end); } } }
7.归并排序
速度仅次于快速排序,内存少的时候使用,可以进行并行计算的时候使用。
选择相邻两个数组成一个有序序列。
选择相邻的两个有序序列组成一个有序序列。
重复第二步,直到全部组成一个有序序列。

public void mergeSort(int[] a, int left, int right) { int t = 1;// 每组元素个数 int size = right - left + 1; while (t < size) { int s = t;// 本次循环每组元素个数 t = 2 * s; int i = left; while (i + (t - 1) < size) { merge(a, i, i + (s - 1), i + (t - 1)); i += t; } if (i + (s - 1) < right) merge(a, i, i + (s - 1), right); } } private static void merge(int[] data, int p, int q, int r) { int[] B = new int[data.length]; int s = p; int t = q + 1; int k = p; while (s <= q && t <= r) { if (data[s] <= data[t]) { B[k] = data[s]; s++; } else { B[k] = data[t]; t++; } k++; } if (s == q + 1) B[k++] = data[t++]; else B[k++] = data[s++]; for (int i = p; i <= r; i++) data[i] = B[i]; }
8.基数排序
用于大量数,很长的数进行排序时。
将所有的数的个位数取出,按照个位数进行排序,构成一个序列。
将新构成的所有的数的十位数取出,按照十位数进行排序,构成一个序列。
代码实现:
public void baseSort(int[] a) { //首先确定排序的趟数; int max = a[0]; for (int i = 1; i < a.length; i++) { if (a[i] > max) { max = a[i]; } } int time = 0; //判断位数; while (max > 0) { max /= 10; time++; } //建立10个队列; List<ArrayList<Integer>> queue = new ArrayList<ArrayList<Integer>>(); for (int i = 0; i < 10; i++) { ArrayList<Integer> queue1 = new ArrayList<Integer>(); queue.add(queue1); } //进行time次分配和收集; for (int i = 0; i < time; i++) { //分配数组元素; for (int j = 0; j < a.length; j++) { //得到数字的第time+1位数; int x = a[j] % (int) Math.pow(10, i + 1) / (int) Math.pow(10, i); ArrayList<Integer> queue2 = queue.get(x); queue2.add(a[j]); queue.set(x, queue2); } int count = 0;//元素计数器; //收集队列元素; for (int k = 0; k < 10; k++) { while (queue.get(k).size() > 0) { ArrayList<Integer> queue3 = queue.get(k); a[count] = queue3.get(0); queue3.remove(0); count++; } } } }
新建测试类进行测试
public class TestSort { public static void main(String[] args) { int []a=new int[10]; for(int i=1;i<a.length;i++){ //a[i]=(int)(new Random().nextInt(100)); a[i]=(int)(Math.random()*100); } System.out.println("排序前的数组为:"+Arrays.toString(a)); Sort s=new Sort(); //排序方法测试 //s.insertSort(a); //s.sheelSort(a); //s.selectSort(a); //s.heapSort(a); //s.bubbleSort(a); //s.quickSort(a, 1, 9); //s.mergeSort(a, 3, 7); s.baseSort(a); System.out.println("排序后的数组为:"+Arrays.toString(a)); } }
部分结果如下:

9.桶排序(Bucket Sort)
要使桶排序正常运行,需要额外的信息:
输入A1,A2,...,AN必须只由小于M的正整数构成,即Ai<M。使用一个大小为M的数组result,初始化为全0。数组有M个单元,即M个桶(bucket)。
public static void bucketSort(int[] a){ //常用写法 int max = Integer.MIN_VALUE; for (int i =0;i<a.length;i++){ max = Math.max(max,a[i]); } int[] bucket = new int[max+1];// 定义桶数组,这个数组的特征是长度是排序数组的最大值+1,为什么要+1?因为不+1桶数组最后一位会下标越界 for (int i =0;i<a.length;i++){ //桶数组此下标有数据,数值就加一 bucket[a[i]]++; } int i = 0; for (int j = 0;j<bucket.length;j++){ while (bucket[j]-->0){ a[i++]=j; } } }
步骤:
result[Ai]中存放的是Ai出现的次数;
读入Ai时,result[Ai]增1;
所有输入数据读入后,扫描数组result,打印出排序后的数据,result[Ai]值是n,Ai就打印n次.
eg.
输入数组{1,4,5,3,7,8,4,9,6,5,0},最大为9,另建一个大小为10的数组,初始化为全0。

读入数组:
遇到1,将result[1]加1
遇到4,将result[4]加1
......
遇到5,将result[5]加1
遇到0,将result[0]加1
得到结果:

打印结果:
0 1 3 4 4 5 5 6 7 8 9
时间复杂度:
算法用时O(M+N),M为桶的个数,N为待排序数组的大小。
空间复杂度:
O(M+N)
如果输入数据非常庞大,桶的数量会非常多,空间代价将会非常大。
如果要进行比较可已加入时间,输出排序时间,从而比较各个排序算法的优缺点,这里不再做介绍。
总结:
一、稳定性:
稳定:冒泡排序、插入排序、归并排序和基数排序
不稳定:选择排序、快速排序、希尔排序、堆排序
二、平均时间复杂度
O(n^2):直接插入排序,简单选择排序,冒泡排序。
在数据规模较小时(9W内),直接插入排序,简单选择排序差不多。当数据较大时,冒泡排序算法的时间代价最高。性能为O(n^2)的算法基本上是相邻元素进行比较,基本上都是稳定的。
O(nlogn):快速排序,归并排序,希尔排序,堆排序。
其中,快排是最好的, 其次是归并和希尔,堆排序在数据量很大时效果明显。
三、排序算法的选择
1.数据规模较小
(1)待排序列基本序的情况下,可以选择直接插入排序;
(2)对稳定性不作要求宜用简单选择排序,对稳定性有要求宜用插入或冒泡
2.数据规模不是很大
(1)完全可以用内存空间,序列杂乱无序,对稳定性没有要求,快速排序,此时要付出log(N)的额外空间。
(2)序列本身可能有序,对稳定性有要求,空间允许下,宜用归并排序
3.数据规模很大
(1)对稳定性有求,则可考虑归并排序。
(2)对稳定性没要求,宜用堆排序
4.序列初始基本有序(正序),宜用直接插入,冒泡
各算法复杂度如下:

排序算法经典题
三色排序
问题描述
输入一个整型数组,每个元素在0~2之间,其中0,1,2分别代表红、白、蓝。现要求对数组进行排序,相同颜色的在一起,而且按红白蓝顺序先后排列。要求时间复杂度为O(n)。
问题分析
最容易想到的是排序,比如快排,归并,堆排等,但它们的时间复杂度为O(nlogn),与题意不符。
第二种想到的是计数排序,扫描一遍过去,分别记录0,1,2的个数,然后再对数组进行赋值。时间复杂度为O(2n),即O(n),满足条件。
还有一种方法,只需扫描一遍数组即可,其充分利用了元素只有3种的特性:在扫描数组的时候,使用首尾俩个指针,分别指示0、1与1、2边界。比如源数组为{2, 2, 0, 0, 1, 1 }。
第一步:首指针p0,尾指针p1,i标识当前扫描位置,当前位置值为2,需要将其交换至尾指针p1位置,p1要向前移动一位,p0、i位置不变。

第二步:i位置值不为0、2,i要向后移动一位,p0、p1位置不变。
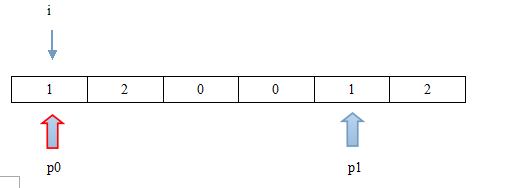
第三步:i位置值为2,需要将其交换至尾指针p1位置,并且p1往前移动一位,i与p0位置不变。

第四步:i位置不为0、2,i要向后移动一位,p0、p1位置不变。
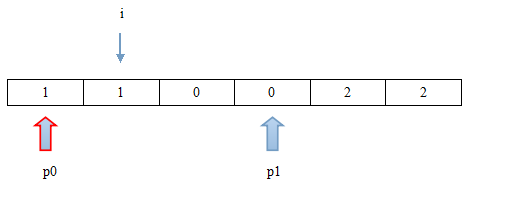
第五步:i位置值为0,需要将其交换至首指针p0位置,并且p0往后移动一位,i与p1位置不变。
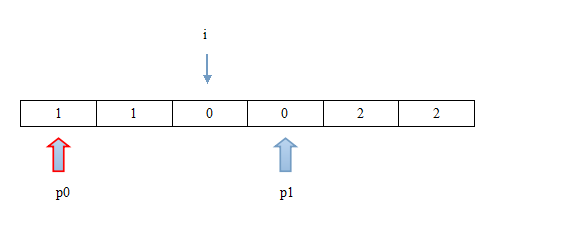
第六步:i位置不为0、2,i要向后移动一位,p0、p1位置不变。
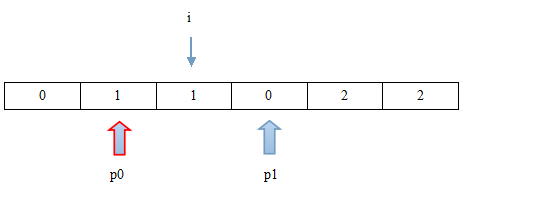
第七步:i位置值为0,需要将其交换至首指针p0位置,并且p0往后移动一位,i与p1位置不变。

第八步:i位置不为0、2,i要向后移动一位,p0、p1位置不变。

第九步:i位置超过p1位置了,结束。
实现代码
public static void sss(int[] a){ // 输入一个整型数组,每个元素在0~2之间,其中0,1,2分别代表红、白、蓝。 // 现要求对数组进行排序,相同颜色的在一起,而且按红白蓝顺序先后排列。要求时间复杂度为O(n)。 // 若为2,值移到尾指针p1,p0和i不变,p1前移一位 // 若为1,i后移一位,p0和p1不变 // 若为0,值移到首指针p0,p1和i不变,p0后移一位, int len = a.length; int p0 = 0;// 首指针 int p1 = len-1;// 尾指针 int i= 0;// 当前位置 int value;// 当前位置的值 while(true) { value = a[i]; if (i>p1) { break; } if (value==0) { a[i]=a[p0]; a[p0]=value; p0++; }else if (value==1) { i++; // value=a[index]; }else if (value==2) { a[i]=a[p1]; a[p1] = value; p1--; } } }
有序矩阵查找
题目:现在有一个行和列都排好序的矩阵,请设计一个高效算法,快速查找矩阵中是否含有值x。给定一个int矩阵mat,同时给定矩阵大小nxm及待查找的数x,请返回一个bool值,代表矩阵中是否存在x。所有矩阵中数字及x均为int范围内整数。保证n和m均小于等于1000。测试样例:[[1,2,3],[4,5,6],[7,8,9]],3,3,10返回:false
思路:等同于Array1: 二维数组中的查找。常识二维数组的写法不要忘记。已知每一行是有序的,每一列也是有序的,最直接的思路是对全部元素进行遍历,时间复杂度显然是O(n*m);这里要利用每行每列有序这个特性来简化问题,从右上角元素开始遍历,如果结点x>a[0,m-1],说明x不在结点这一行中,于是下一次从a[1,m-1]元素进行比较;如果x<a[0,m-1],说明x不在结点这一列中,于是从a[0,m-2]结点开始遍历,即通过将x与当前矩阵的右上角a[p,q]元素进行比较,如果x小,那么排除右上角结点所在列,即对q--;如果x大,那么排除右上角结点所在行,即进行p++,直到p>n-1或者q<0时结束。这样的时间复杂度是O(n+m)
即最多只需要与n+m个结点进行比较即可作出判断。
实现代码
/** * 有序矩阵查找 * @param a * @param x 要比较的数 */ public static boolean sss(int[][] a,int x){ int ni = 0;// 横坐标下标 int mi = m-1;// 纵坐标下标 int t = 0; boolean result = true; // int test = 0; while (true) { // System.out.println("测试需要循环几次:"+(++test)); if (ni>mi) { result = false; break; } if (x>a[ni][mi]) { ni++; }else if(x<a[ni][mi]){ mi--; }else{ // 相等直接返回 break; } } return result; }
需要排序的最短子数组
题目
对于一个数组,请设计一个高效算法计算需要排序的最短子数组的长度。
给定一个int数组A和数组的大小n,请返回一个二元组,代表所求序列的长度。(原序列位置从0开始标号,若原序列有序,返回0)。保证A中元素均为正整数。
测试样例:[1,4,6,5,9,10],6
返回:2
思路
从左开始遍历数组,记录下已经遍历部分的最大值max,如果遍历的数值小于max时,记录这种情况下最右的位置right。
从左开始遍历数组,记录下已经遍历部分的最大值min,如果遍历的数值大于min时,记录这种情况下最右的位置left。
代码实现
public int shortestSubsequence(int[] A, int n) { int max=A[0],min=A[n-1]; int right=0,left=0; for(int i=0;i<n;i++){ max=Math.max(max,A[i]); if(A[i]<max){ right=i; } } for(int i=n-1;i>=0;i--){ min=Math.min(min,A[i]); if(A[i]>min){ left=i; } } return right==left?0:right-left+1; }
排序数组中的相邻两数最大差值
题目
给定一个数组A及其大小n,求其排序后的相邻两数的最大差值。(注:要求时间复杂度为O(n))
思路
题目要求对排序后的数组进行操作,显然需要先对数组进行排序。如果没有要求时间复杂度,那么可以有很多种排序算法,如快速排序、堆排序、归并排序等等。但是这里要求时间复杂度为O(n),就不能用上述常规的排序算法了。
那么桶排序可以吗?由于我们不知道最大数的位数,因此,如果最大数的位数很大的话,我们就需要成千上万个桶,显然对空间要求太大。我们可以利用桶排序的思想,利用它的变种:
1) 首先求出数组的最大值max和最小值min;
2) 然后将该区间均等的划分为n+1份,即n+1个桶,那么由于只有n个数,因此,必定至少有一个桶为空桶;
3) 遍历数组,将所有数入桶,并记录每一个桶的最大值和最小值;
4) 不用考虑桶内数的差值,因为它都不会大过空桶两边的桶的数的差值;
5) 依次遍历每一个桶,找到一个空桶,记录其前一个非空桶的最大值和其后一个非空桶的最小值,它们的差值就是最大的(考虑有多个空桶的情况)。
代码实现
public static int maxGap(int[] nums) { if (nums == null || nums.length < 2) { return 0; } int len = nums.length; int min = Integer.MAX_VALUE; int max = Integer.MIN_VALUE; for (int i = 0; i < len; i++) { min = Math.min(min, nums[i]); max = Math.max(max, nums[i]); } if (min == max) { return 0; } boolean[] hasNum = new boolean[len + 1]; int[] maxs = new int[len + 1]; int[] mins = new int[len + 1]; int bid = 0; for (int i = 0; i < len; i++) { bid = bucket(nums[i], len, min, max); // 算出桶号 mins[bid] = hasNum[bid] ? Math.min(mins[bid], nums[i]) : nums[i]; maxs[bid] = hasNum[bid] ? Math.max(maxs[bid], nums[i]) : nums[i]; hasNum[bid] = true; } int res = 0; int lastMax = 0; int i = 0; while (i <= len) { if (hasNum[i++]) { //找到第一个不为空的桶 lastMax = maxs[i - 1]; break; } } for (; i <= len; i++) { if (hasNum[i]) { res = Math.max(res, mins[i] - lastMax); lastMax = maxs[i]; } } return res; } //使用long类型是为了防止相乘时溢出 public static int bucket(long num, long len, long min, long max) { return (int) ((num - min) * len / (max - min)); }
有序数组合并
题目
有两个从小到大排序以后的数组A和B,其中A的末端有足够的缓冲空格容纳B。请编写一个方法将B合并入A并排序。
给定两个有序int数组A和B,其中A的缓冲空用0填充,同时给定A和B的真实大小int m和int n,请返回合并后的数组。
解法一:
从结尾开始归并,不会覆盖元素。从A[n+m-1]处开始往前一个元素一个元素的求,每次都要比较A[i]和B[j]的大小。
需要注意的是,要考虑到: A和B有一个为空时的情况
public static void merge(int[] a,int[] b,int m,int n){ int i , j , k ; for( i = m - 1, j = n - 1, k = n + m -1; k >= 0; k--){ if( i >= 0 &&(j < 0 || a[i] >= b[j]) ) a[k] = a[i--]; else a[k] = b[j--]; } }
解法二:
算法思想是:由于合并后A数组的大小必定是m+n,所以从最后面开始往前赋值,先比较A和B中最后一个元素的大小,把较大的那个插入到m+n-1的位置上,再依次向前推。如果A中所有的元素都比B小,那么前m个还是A原来的内容,没有改变。如果A中的数组比B大的,当A循环完了,B中还有元素没加入A,直接用个循环把B中所有的元素覆盖到A剩下的位置。代码如下:
public static void merge(int[] a,int[] b,int m,int n){ int count = m + n - 1; --m; --n; while (m >= 0 && n >= 0) a[count--] = a[m] > b[n] ? a[m--] : b[n--]; while (n >= 0) a[count--] = b[n--]; }
测试
public static void main(String[] args) { int[] a = new int[]{1,4,7,16,25,27,0,0,0,0,0}; int[] b = new int[]{3,4,8,11,20}; merge(a, b, 6, 5); for (int i = 0; i < a.length; i++) { System.out.print(a[i]+"\t"); } }
未完


