算法Sedgewick第四版-第1章基础-1.4 Analysis of Algorithms-001分析步骤

 

For many programs, developing a mathematical model of running time
reduces to the following steps:
■Develop an input model, including a definition of the problem size.
■ Identify the inner loop.
■ Define a cost model that includes operations in the inner loop.
■Determine the frequency of execution of those operations for the given input.
Doing so might require mathematical analysis—we will consider some examples
in the context of specific fundamental algorithms later in the book.
If a program is defined in terms of multiple methods, we normally consider the
methods separately. As an example, consider our example program of Section 1.1,
BinarySearch .
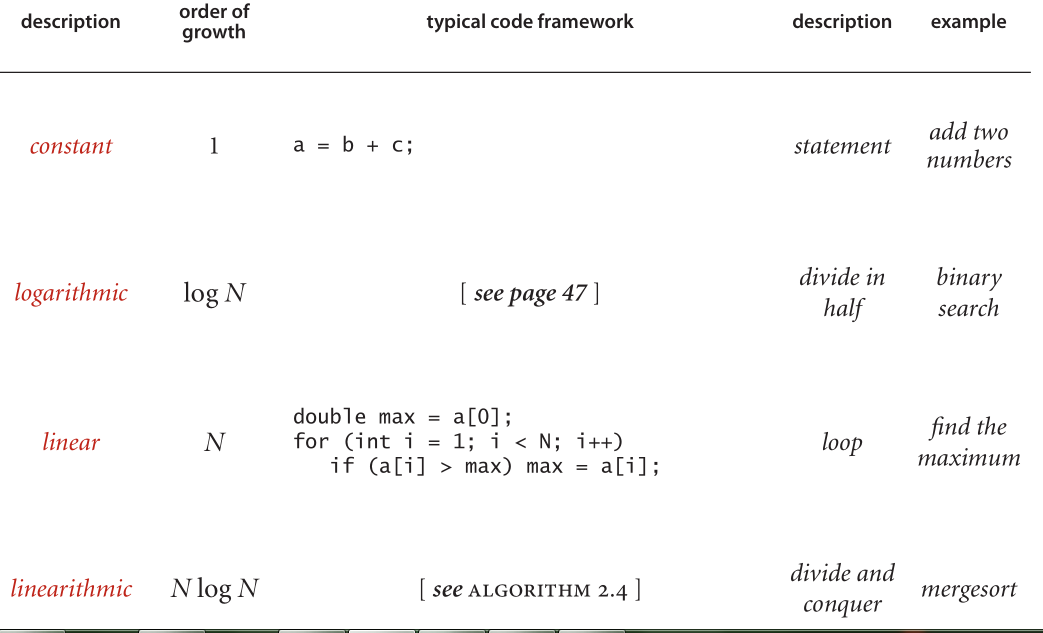
Binary search. The input model is the array a[] of size N; the inner loop is the
statements in the single while loop; the cost model is the compare operation
(compare the values of two array entries); and the analysis, discussed in Section
1.1 and given in full detail in Proposition B in Section 3.1, shows that the num-
ber of compares is at most lg N ? 1.
Whitelist. The input model is the N numbers in the whitelist and the M numbers
on standard input where we assume M >> N; the inner loop is the statements in
the single while loop; the cost model is the compare operation (inherited from
binary search); and the analysis is immediate given the analysis of binary search—
the number of compares is at most M (lg N ? 1).
Thus, we draw the conclusion that the order of growth of the running time of the
whitelist computation is at most M lg N , subject to the following considerations:
■ If N is small, the input-output cost might dominate.
■The number of compares depends on the input—it lies between ~M and ~M
lg N, depending on how many of the numbers on standard input are in the
whitelist and on how long the binary search takes to find the ones that are (typi-
cally it is ~M lg N ).
■ We are assuming that the cost of Arrays.sort() is small compared to M lg N.
Arrays.sort() implements the mergesort algorithm, and in Section 2.2, we
will see that the order of growth of the running time of mergesort is N log N
(see Proposition G in chapter 2), so this assumption is justified.
Thus, the model supports our hypothesis from Section 1.1 that the binary search algo-
rithm makes the computation feasible when M and N are large. If we double the length
of the standard input stream, then we can expect the running time to double; if we
double the size of the whitelist, then we can expect the running time to increase only
slightly.