圆圈舞蹈 题解
圆圈舞蹈
[问题描述]
熊大妈的奶牛在时针的带领下，围成了一个圆圈跳舞。由于没有严格的教育，奶牛们之间的间隔不一致。
奶牛想知道两只最远的奶牛到底隔了多远。奶牛A到B的距离为A顺时针走和逆时针走，到达B的较短路程。告诉你相邻两个奶牛间的距离，请你告诉奶牛两只最远的奶牛到底隔了多远。
［输入］
第一行一个整数N，表示有N只奶牛。（2<=N<=100000）
接下来2～N+1行，第i行有一个数，表示第i-1头奶牛顺时针到第i头奶牛的距离。
（1<=距离<=maxlongint,距离和<=maxlongint）
第N+1行的数表示第N头奶牛顺时针到第1头奶牛的距离。
［输出］
一行，表示最大距离
［样例］
circle.in
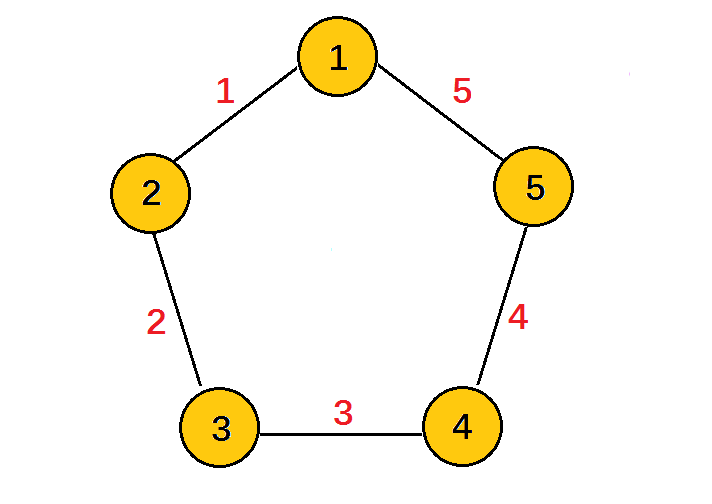
5
1
2
3
4
5
circle.out
7
[样例解析]
Circle.out所有奶牛i到j之间的距离和到达方式（顺为顺时针，逆为逆时针）如下：
|
|
1 |
2 |
3 |
4 |
5 |
|
1 |
0 |
1（顺） |
3（顺） |
6（顺） |
5（逆） |
|
2 |
1（逆） |
0 |
2（顺） |
5（顺） |
6（逆） |
|
3 |
3（逆） |
2（逆） |
0 |
3（顺） |
7（顺） |
|
4 |
6（逆） |
5（逆） |
3（逆） |
0 |
4（顺） |
|
5 |
5（顺） |
6（顺） |
7（逆） |
4（逆） |
0 |
——————————————————分割线—————————————————
SOLUTION
朴素想法：枚举环上两点求距离，复杂度O ( n2 ) , n =105时间无法承受。
改进想法：朴素想法有大量不必要的重复计算，乱搞一下，复杂度O( n ) .
1 #include "iostream" 2 3 using namespace std ; 4 typedef long long QAQ ; 5 const long long INF = 1000000000 ; 6 const int maxN = 1e5 + 1e3 ; 7 8 inline QAQ gmax ( QAQ x , QAQ y ) { return x > y ? x : y ; } 9 QAQ S[ maxN ] ; 10 11 inline int INPUT ( ) { 12 int x = 0 , f = 1 ; char ch = getchar ( ) ; 13 while ( ch < '0' || '9' < ch ) { if ( ch == '-' ) f = -1 ; ch = getchar ( ) ; } 14 while ( ch >= '0' && ch <= '9' ) { x = ( x << 1 ) + ( x << 3 ) + ch -'0' ; ch = getchar ( ) ; } 15 return x * f ; 16 } 17 18 int main ( ) { 19 freopen ( "circle.in" , "r" , stdin ) ; 20 freopen ( "circle.out" , "w" , stdout ) ; 21 int N = INPUT ( ) ; 22 for ( int i=1 ; i<=N ; ++i ) { 23 S[ i ] = S[ i - 1 ] + INPUT ( ) ; 24 } 25 QAQ Ans = -INF ; 26 int L = 1 , R = 1 ; 27 while ( L <= R && R <= N ) { 28 unsigned long long Dis = S[ R ] - S[ L ] ; 29 if ( ( Dis << 1 ) <= S[ N ] ) { 30 ++R ; Ans = gmax ( Dis , Ans ) ; 31 } 32 else { 33 ++L , Ans = gmax ( S[ N ] - Dis , Ans ) ; 34 } 35 } 36 cout << Ans << endl ; 37 return 0 ; 38 }
2016-10-17 17:24:49
