浅谈 LCA
LCA问题
一.概述：
在图论与计算科学中，两个节点 v 与 w 在有向无环图( directed acyclic graph , DAG )或树中的最近公共祖先(Lowest common anccestor , LCA ) 是这两个节点 v 与 w 的深度最深的祖先。我们定义，该深度最深的节点为 v 与 w 的最近公共最先，即LCA 。
例如，在下图中
LCA ( A , B ) = F , LCA ( A , G ) = C , LCA ( B , D ) = C , LCA ( C , G ) = C ;
[ATTENTION]:两个节点的LCA在两点间的路径上。
二.求解方法
方法一：
将LCA问题转化为RMQ问题(区间最值问题)。
1).从任意一个节点开始，对图进行深度优先遍历，记录每个节点的欧拉序，深度，第一次被遍历fst[]时间等信息。
2).将每个节点的深度按照欧拉序列加入一个数组中，即每次经过一个节点时，都将其加入数组。
3).如果fst[ v ] < fst[ u ] ,则LCA( v , u ) = RMQ ( fst[ v ] , fst[ u ] )
如果fst[ v ] > fst[ u ] ,则LCA( v , u ) = RMQ ( fst[ u ] , fst[ v ] )
以上就是主要思路，下面举个栗子：
当查询A 与 D 的 LCA 时 ， LCA ( A , D ) = RMQ ( fst[ D ] , fst[ A ] )
即，区间 [ fst[ D ] , fst[ A ] ] 的深度最小值 , 这段区间[ 2 , 7 ] ，(2 ，1 ，2 ，1 ，2 ，3)中最小值是1，1对C应的节点是C，则A，D的LCA是C 。
[ATTENTION]:区间最值的关键字是深度.
那么现在的问题就是解决RMQ问题，通常使用ST算法(RMQ问题之ST算法)或线段树解决,本文使用线段树解决这个问题。
核心代码&注释：
1 inline void Add_Edge ( int x , int y , int _val ){//邻接表建图 2 e[ ++cnt ].to = y ; 3 e[ cnt ].val = _val ; 4 e[ cnt ].next = head[ x ] ; 5 head[ x ] = cnt ; 6 } 7 8 void Build_Tree ( int x , int y , int i ) {//线段树建树 9 tr[ i ].l = x ; tr[ i ].r = y ; 10 if ( x==y ) tr[ i ].mintr = dep[ x ] , tr[ i ].pos = x ;//按照深度建树 11 else { 12 QAQ mid = ( tr[ i ].l + tr[ i ].r ) >>1 ; 13 Build_Tree ( x , mid , i<<1); 14 Build_Tree ( mid+1 , y , i<<1|1); 15 if (tr[i<<1].mintr > tr[i<<1|1].mintr )//tr[].mintr表示这个区间最小值 ，tr[].pos表示最小值所在位置 16 tr[ i ].pos = tr[i<<1|1].pos,tr[ i ].mintr = tr[i<<1|1].mintr; 17 else 18 tr[ i ].pos = tr[ i<<1 ].pos,tr[ i ].mintr = tr[ i<<1 ].mintr; 19 } 20 21 } 22 23 void DFS ( int x , int depth ) { 24 vis[ x ] = true ; 25 ver[ ++dfs_num ] = x ; //欧拉序 26 fst[ x ] = dfs_num ; //第一次出现位置 27 dep[ dfs_num ] = depth ;//该节点深度 28 for ( int i=head[ x ] ; i ; i=e[i].next ) { 29 int temp = e[ i ].to ; 30 if ( !vis[ temp ] ){ 31 DFS ( temp , depth + 1 ) ; 32 ver[ ++dfs_num ] = x ; 33 dep[ dfs_num ] = depth ; 34 } 35 } 36 } 37 38 void Query_Min ( int q , int w , int i ) { 39 if(q <= tr[i].l && w >= tr[i].r ){ 40 if (tr[ i ].mintr < min_val ){ 41 min_val = tr[i].mintr ;// 记录最小值 42 min_pos = tr[i].pos ;// 记录最小值所在位置 43 } 44 } 45 else { 46 QAQ mid = (tr[i].l + tr[i].r ) >> 1; 47 if(q > mid) { 48 Query_Min ( q , w , i << 1 | 1); 49 } 50 else if(w <= mid) { 51 Query_Min ( q , w , i << 1); 52 } 53 else { 54 Query_Min ( q , w , i << 1) ; 55 Query_Min ( q , w , i << 1 | 1); 56 } 57 } 58 } 59 60 int LCA ( int x , int y ) { 61 int px = fst[ x ] , py = fst[ y ] , tmp ; 62 min_val = INF ;//初始化 63 if ( py < px ) swap ( px , py ) ; 64 Query_Min ( px , py , 1 ) ; 65 return ver[ min_pos ] ;//最小值在欧拉序中对应节点即为LCA 66 } 67 int main ( ) { 68 int N ,M ; 69 scanf ("%d",&N); 70 for ( int i=1 ; i<=N-1 ; ++i ) { 71 int _x , _y , __ ; 72 scanf("%d %d %d" , &_x , &_y ,&__ ) ; 73 Add_Edge ( _x , _y , __ ) ; 74 Add_Edge ( _y , _x , __ ) ; 75 } 76 DFS ( 1 , 1 ) ; 77 Build_Tree ( 1 , dfs_num , 1 ) ; 78 DEBUG_( dfs_num ) ; 79 scanf ("%d",&M); 80 for ( int i=1 ; i<=M ; ++i ) { 81 int u , v ; 82 scanf ( "%d%d" , &u , &v ) ; 83 printf ("%d",LCA ( u , v ) ) ; 84 putchar('\n'); 85 } 86 return 0 ; 87 }
————————————————分割线————————————————
方法二：
倍增算法求LCA.
倍增算法的核心在于father[][]数组，father[ i ] [ j ] 表示从节点 i 开始，向上第2j个节点编号。
可以通过以下的式子推出
father[ x ][ i ] = father[ father[ x ][ i - 1 ] ][ i - 1 ] ;
如下图，求节点 7 与 节点 15 的LCA 。
首先找到深度较深的节点15 ， 让该节点向上移动，因为LCA一定在两节点的路径上。通过倍增思想，让该节点向上移动，使两个节点的深度相同。
if ( dep[ x ] < dep[ y ] )gswap( x , y ) ; int t = dep[ x ] - dep[ y ] ; for ( int i=0 ; i<=20 ; ++i ) if( ( 1 << i ) & t ) x = father[ x ][ i ] ;
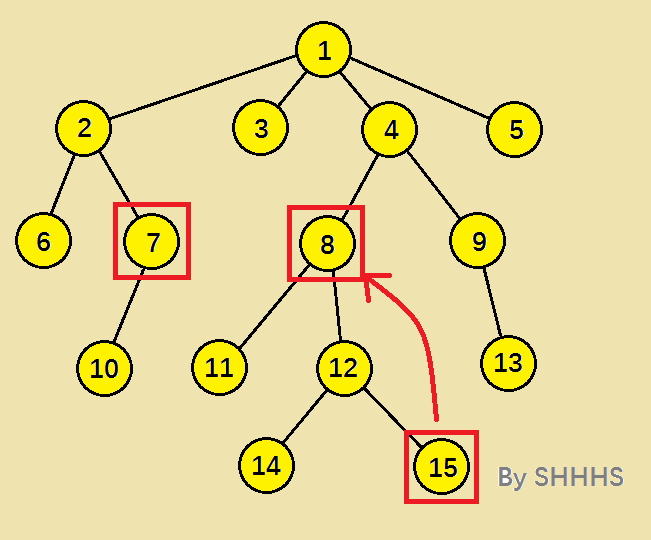
这时，两个节点深度相同，仍然通过倍增思想，让两节点以相同的速率向上跳，跳到两个节点的父节点恰好相等。
if( x == y ) return x ;//蜜汁特判 for ( int i=20 ; i>=0 ; --i ) { if ( father[ x ][ i ] == father[ y ][ i ] ) continue ;//跳多了，换一个小一点的值 x = father[ x ][ i ] ;//两个节点以相同速率向上跳 y = father[ y ][ i ] ;// }
这时，两个节点的父节点就是LCA，直接返回父节点即可，算法结束。
[ATTENTION] : 这里需要加一个特判，如果两个节点调到同一位置直接返回。
核心代码&注释：
1 inline void gswap ( int &x , int &y ) { int temp = x ; x = y ; y = temp ; } 2 3 int cnt ; 4 5 void Add_Edge ( const int x , const int y , const int val ) {//建边 6 e[ ++cnt ].to = y ; 7 e[ cnt ].val = val ; 8 e[ cnt ].next = head[ x ] ; 9 head[ x ] = cnt ; 10 } 11 12 void DFS ( int x ) { 13 vis[ x ] = true ; 14 for ( int i=1 ; i<=20 ; ++i ) { 15 if ( dep[ x ] < ( 1 << i ) ) break ; 16 father[ x ][ i ] = father[ father[ x ][ i - 1 ] ][ i - 1 ] ;//father数组的递推 17 } 18 for ( int i=head[ x ] ; i ; i=e[ i ].next ) {//图的DFS 19 int temp = e[ i ].to ; 20 if ( vis[ temp ] )continue ; 21 else { 22 Dis [ temp ] = Dis [ x ] + e[ i ].val ; 23 father[ temp ][ 0 ] = x ; 24 dep[ temp ] = dep[ x ] + 1 ; 25 DFS ( temp ) ; 26 } 27 } 28 } 29 int LCA ( int x , int y ) { 30 if ( dep[ x ] < dep[ y ] )gswap( x , y ) ; 31 int t = dep[ x ] - dep[ y ] ;//深度差 32 for ( int i=0 ; i<=20 ; ++i ) if( ( 1 << i ) & t ) x = father[ x ][ i ] ;//让深度较大的节点跳至深度相等 33 if( x == y ) return x ;//蜜汁特判 34 for ( int i=20 ; i>=0 ; --i ) {//两个节点同速率向上跳 到父亲恰好相等 35 if ( father[ x ][ i ] == father[ y ][ i ] ) continue ; 36 x = father[ x ][ i ] ; y = father[ y ][ i ] ; 37 } 38 return father[ x ][ 0 ] ;// 返回父节点 39 } 40 41 int main ( ) { 42 int N , Q ; 43 scanf ( "%d" , &N ) ; 44 for ( int i=1 ; i<=N-1 ; ++i ) {//读入建边 45 int _x , _y , _val ; 46 scanf ( "%d%d%d" , &_x , &_y , &_val ) ; 47 Add_Edge ( _x , _y , _val ) ; 48 Add_Edge ( _y , _x , _val ) ; 49 } 50 dep[ 1 ] = 1 ;// 51 DFS ( 1 ) ;//以1为根节点DFS 52 scanf ( "%d" , &Q ) ; 53 while ( Q-- ) { 54 int _x , _y ; 55 scanf ( "%d%d" , &_x , &_y ) ; 56 printf ( "%d\n" ,LCA ( _x , _y ) ) ; 57 } 58 }
—————————————分割线—————————————
方法二：
树的路径剖分算法求LCA。
(不懂树链剖分点这，树链剖分——精讲)
对于一棵树，我们将其剖分为若干条链，记录每个节点所在链的链头，该节点的父节点。
当查询两节点LCA时
伪代码：
while ( x 与 y 不在同一条链上 )
if ( x的DFS序 > y的DFS序 )x = pre [ start[ x ] ] //通过链头跳到另一条链上
else if ( x的DFS序 < y的DFS序 )y = pre [ start[ y ] ]
if ( x的DFS序 > y的DFS序 ) print ( y )
if ( x的DFS序 < y的DFS序 ) print ( x )
算法图示：
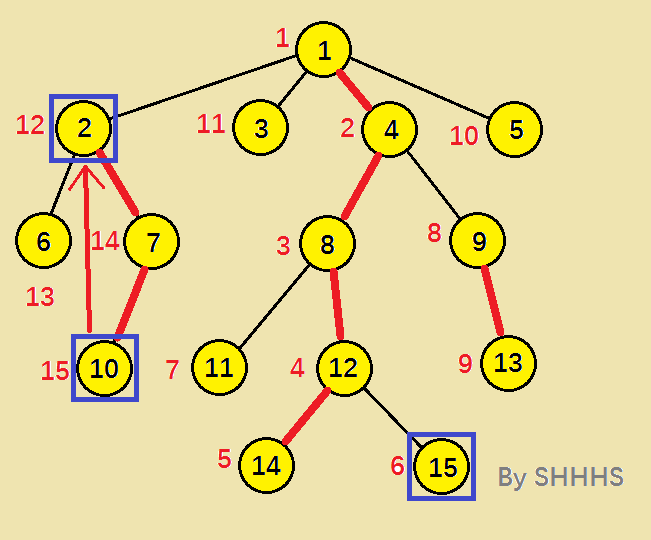
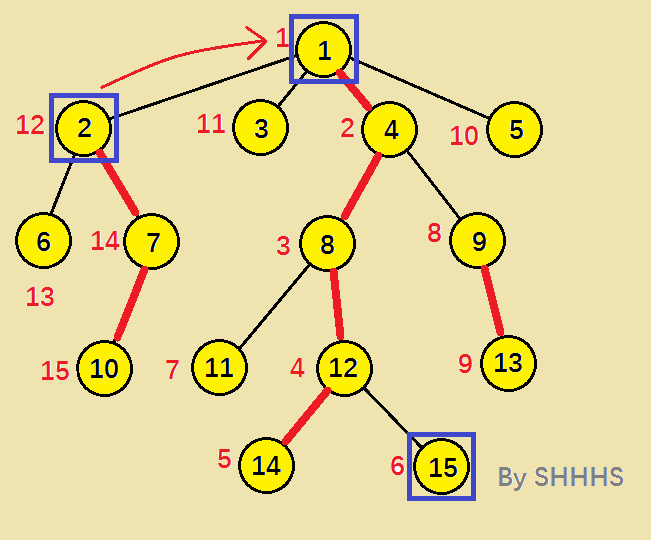
动态图：
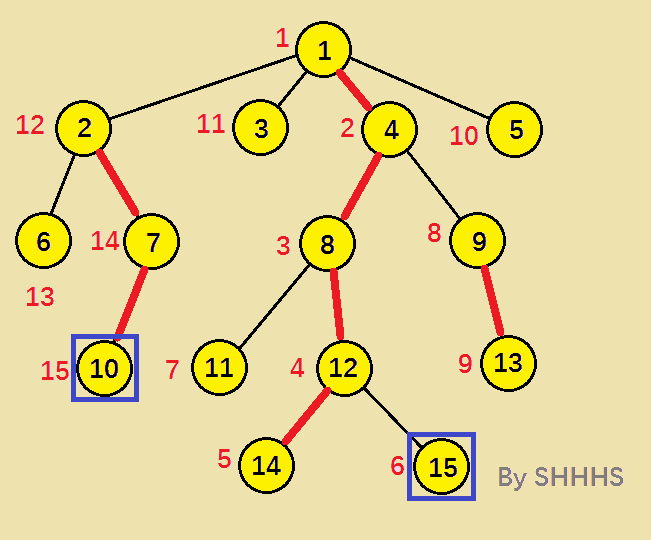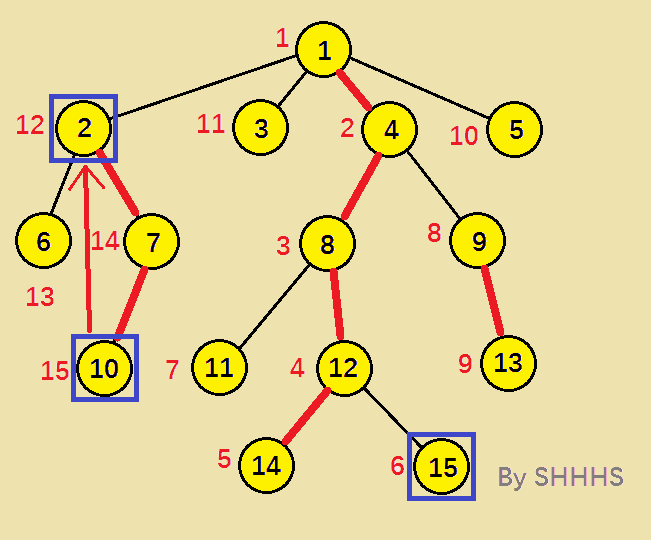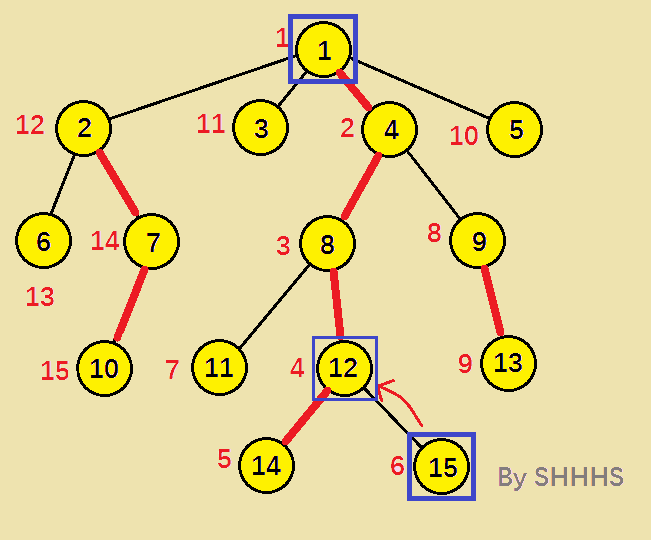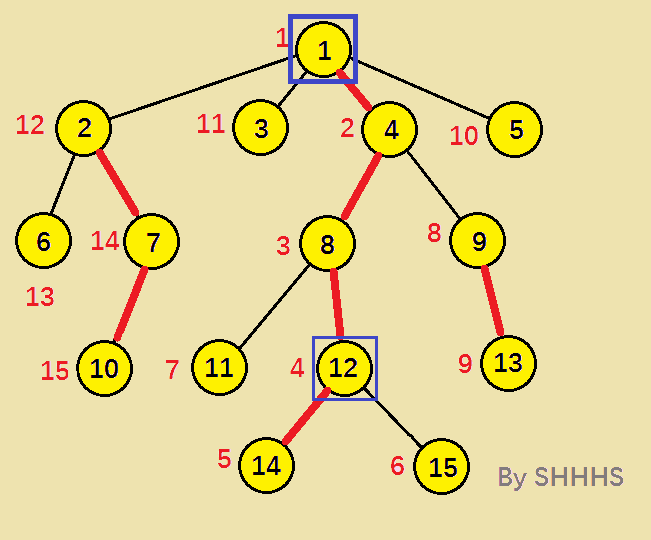
至此，两个节点在同一条链上，算法结束，DFS序较小的节点 1 即为LCA 。
算法模板&注释：
1 void Add_Edge ( const int _x , const int _y , const int _val ) { 2 e[ ++cnt ].to = _y ; 3 e[ cnt ].val = _val ; 4 e[ cnt ].next = head[ _x ] ; 5 head[ _x ] = cnt ; 6 } 7 8 int Init_DFS ( const int x , const int father ) { 9 int cnt_ , max_ = 0 ; 10 for ( int i=head[ x ] ; i ; i=e[ i ].next ) { 11 int temp = e[ i ].to ; 12 if ( temp==father ) continue ; 13 Dis[ temp ] = Dis[ x ] + e[ i ] .val ; 14 int _ = Init_DFS ( temp , x ) ; 15 if ( _ > max_ ) {max_ = _ ; hv[ x ] = temp ;} 16 cnt_ +=_; 17 } 18 return cnt_ ; 19 } 20 21 void DFS ( const int x , const int father ) { 22 if ( !start[ x ] ) start[ x ] = start[ father ] ; 23 DFN[ x ] = ++dfs_num ; 24 if ( hv[ x ] ) DFS ( hv[ x ] , x ) ; 25 for ( int i=head[ x ] ; i ; i =e[ i ].next ) { 26 if ( e[ i ].to != hv[ x ] && e[i].to != father ) { 27 int temp = e[ i ].to ; 28 start[ temp ] = temp ; 29 pre [ temp ] = x ; 30 DFS ( temp , x ) ; 31 } 32 } 33 } 34 35 int LCA ( const int x , const int y ) {//start[]数组表示该点所在链的链头 36 int px = x , py = y ; 37 while ( start[ px ] != start[ py ] ) {//不在一条链上 38 if ( DFN[start[px]]>DFN[start[py] ] ) {//DFS序较大的跳 39 px = pre[ start[px] ] ; 40 } 41 else { 42 py = pre[ start[py] ] ; 43 } 44 } 45 return DFN[ px ] > DFN[ py ] ? py : px ;//返回DFS序较小的节点即为LCA 46 }
———————————————分割线———————————————
方法四：
Tarjan算法求LCA.
[ATTENTION]:LCA的Tarjan算法与强连通分量的Tarjan算法无关。
2016-10-06 23:01:23
(完)
