NOIP欢乐模拟赛 T2 解题报告

小澳的坐标系

（coordinate.cpp/c/pas）

【题目描述】

小澳者表也，数学者景也，表动则景随矣。

小澳不喜欢数学，可数学却待小澳如初恋，小澳睡觉的时候也不放过。

小澳的梦境中出现了一个平面直角坐标系，自原点，向四方无限延伸。

小澳在坐标系的原点，他可以向上、向左或者向右走。他可以走n步，但不能经过相同的点。

小澳想知道他有多少种走法。

 

【输入格式】

输入文件名为coordinate.in。

输入文件仅第一行一个正整数n，表示小澳可以走的步数。

 

【输出格式】

输出文件名为coordinate.out。

输出文件共一行，输出一个正整数，表示答案（对10^9+7取模）。

 

【输入输出样例1】

coordinate.in

coordinate.out

2

7

 

【输入输出样例1说明】

从(0,0)出发走2步，共7种走法：

(0,0)->(0,1)->(0,2)

(0,0)->(0,1)->(1,1)

(0,0)->(0,1)->(-1,1)

(0,0)->(1,0)->(2,0)

(0,0)->(1,0)->(1,1)

(0,0)->(-1,0)->(-2,0)

(0,0)->(-1,0)->(-1,1)

 

【输入输出样例2】

coordinate.in

coordinate.out

3

17

 

 

【数据规模与约定】

测试点编号

n

1~2

n<=10

3~4

n<=100

5~6

n<=1000

7~8

n<=10^6

9~10

n<=10^9

 

————————————————————————分割线————————————————————————

分析：

看到这道题不难想到他的递推式

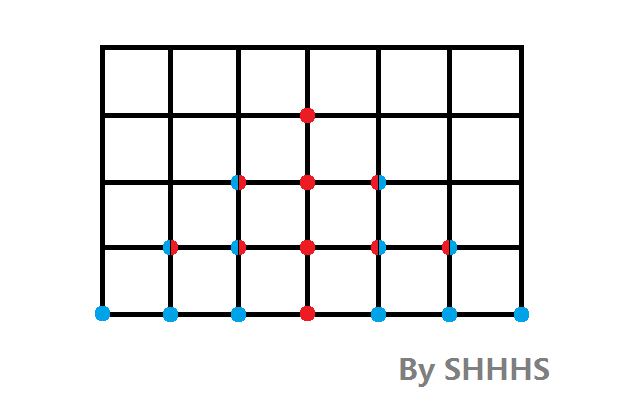
在上图，蓝点表示只有两种走法的点，红点表示三种走法的点，红蓝相间表示两种都有。

普通递推式如下 ( 80分 )：

F[i][0]=F[i-1][0]+F[i-1][1]*2

F[i][1]=F[i-1][0]+F[i-1][1] 

 

 1 #include "bits/stdc++.h"
 2 
 3 using namespace std ;
 4 typedef long long QAQ ;
 5 const int MOD = 1e9 + 7 ;
 6 
 7 int main ( ) {
 8         QAQ t1 = 1 , t2 = 3 , t3 = 3 , N ;
 9         cin >> N ;
10         --N ;
11         for ( int i=1 ; i<=N ; ++i ) {
12                 t3 = ( t2 - t1 ) * 2 + t1 * 3 ;
13                 t1 = t2 ;
14                 t2 = t3 ;
15         }    
16         cout << t3 << endl ;
17         return 0 ;
18 }
View Code

 

但是，我们发现每一步只与上一步有关，可以建立递推关系，构造矩阵+快速幂解决。( AC )

 

 

 1 #include "bits/stdc++.h"
 2  
 3 using namespace std;
 4 typedef long long QAQ ;
 5 const int MOD = 1e9 + 7 ;
 6 
 7 struct Matrix{
 8         QAQ v[2][2];
 9         Matrix ( ) { memset ( v , 0 , sizeof ( v ) ) ; }
10 }base , ans ;
11 
12 Matrix operator*( Matrix x , Matrix y ) {
13         Matrix res;
14         for(int i=0;i<2;i++)
15         for(int j=0;j<2;j++)
16         for(int k=0;k<2;k++)
17                 (res.v[i][j]+=(x.v[i][k]*y.v[k][j]%MOD))%=MOD;
18         return res;
19 }
20 
21 int main ( ) {
22         int N ;
23         scanf ( "%d" , &N ) ; 
24         ans.v[ 0 ][ 0 ] = 1 ;
25         base.v[ 0 ][ 0 ] = base.v[ 0 ][ 1 ] = base.v[ 1 ][ 1 ] = 1 ;
26         base.v[ 1 ][ 0 ] = 2 ;
27         for ( int i=N + 1 ; i ; i>>=1 , base = base * base )
28                 if  ( i & 1 ) ans = ans * base ;
29         printf( "%I64d\n" , ans.v[0][0] ) ;
30         return 0 ;
31 }
Matrix

2016-10-03 21:42:08 

 PS:本题可以进一步化简递推,可得 f ( n ) = 2 * f ( n - 1 ) + f ( n - 2 ) ,也可得到答案。

(完)

 

posted @ 2016-10-03 21:45  SHHHS  阅读(329)  评论(0)  编辑  收藏  举报