DFT与IDFT

 

【转】https://blog.csdn.net/mingzhuo_126/article/details/88044390

 

 

二.编程实现
考滤到DFT和IDFT算法过程中有部分相似，可以把它们合成到一个算法。

/*
    x-存放要变换数据的实部
    y-存放要变换数据的虚部
    a-存放变换结果的实部
    b-存放变换结果的虚部
    n-数据长度
    sign-为1时执行DFT，为-1时执行IDFT
*/
#include "math.h"
void dft(x,y,a,b,n,sign)
int n, sign;
double x[],y[],a[],b[];
{
    int i,k;
    double c,d,q,w,s;
    q = 6.28318530718/n;
    for (k=0;k<n;k++)
    {
        w=k*q;
        a[k]=b[k]=0.0;
        for(i=0;i<n;i++)
        {
            d=i*w;
            c=cos(d);
            s=sin(d)*sign;
            a[k]+=c*x[i] + s*y[i];
            b[k]+=c*y[i] - s*x[i];
        }
    }
    if(sign == -1)
    {
        c=1.0/n;
        for (k=0;k<n;k++)
        {
            a[k]=c*a[k];
            b[k]=c*b[k];
        }
    }
}

下面验证此算法，对X(n)=(0,1,2,3,4,5,6,7)，做DFT和IDFT算法

dft_d.c

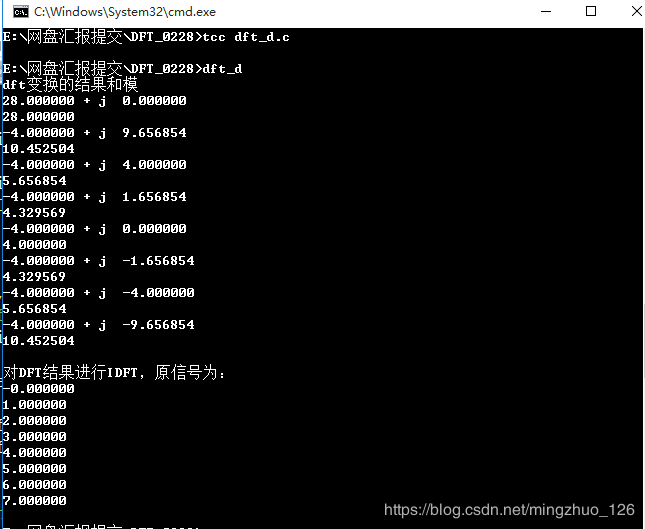
#include "stdio.h"
#include "math.h"
#include "dft.c"
#define N 4
static double  x[N],y[N],a[N],b[N],c[N];
main(){
    int k;
    int i=0;
    for(i=0; i<N; i++)
    {
        x[i]=i;
        y[i]=0;
        
        
    }
    dft(x,y,a,b,N,1);    //DFT变换
    for(i=0; i<N; i++)
    {
        c[i]=sqrt(a[i]*a[i]+b[i]*b[i]);    //算出模
        printf("%lf + j  %lf \n",a[i],b[i]);//输出变换后结果                
        printf("%lf \n",c[i]); //输出模值
        printf("\n");        
    }
    dft(a,b,x,y,N,-1); //IDFT变换
    for(i=0; i<N; i++)
    {
        printf("%lf \n",x[i]); //输出x(n)的实部
    }
    
}

运行结果：