CRDT概述
what:
object: 可以理解为“副本”;
operation: 操作接口,由客户端调用,分为两种,读操作query和写操作update;
query: 查询操作,仅查询本地副本;
update: 更新操作,先尝试进行本地副本更新,若更新成功则将本地更新同步至远端副本;
merge: update在远端副本的合并操作;
where:
如果一个场景的update操作本身满足以上三律(交换、结合、幂等),merge操作仅需要对update操作进行回放即可,这种形式称为op-based CRDT。最简单的例子是集合求并集,如下:

如果场景中的update无法满足3定律,则需要考虑在副本数据上,加上元数据,从而让update和merge操作具备以上三律,这种形式称为state-based CRDT。加上元信息,从而让其满足条件的方式是让其更新保持“单调”,这个关系一般被称为“偏序关系”。举一个简单例子,每次update操作都带上时间戳,在merge时对本地副本时间戳及同步副本时间戳进行比对,取更新的结果,这样总能保证结果最新并且最终一致,这种方式称为Last Write Wins:
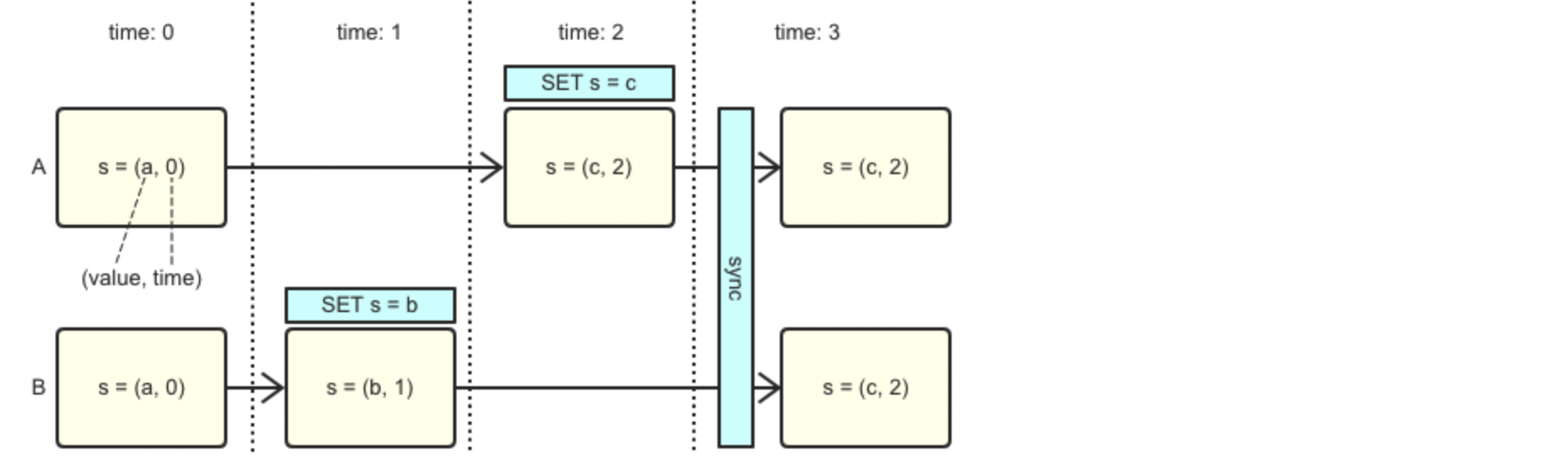
有两点值得注意的地方:
- update操作无法满足三律,如果能将元信息附加在操作或者增量上,会是一个相对op-based方案更优化的选择
- 如果同步过程能确保exactly once的语义,幂等律条件是可以被放宽,比如说加法本身满足交换律结合律但不幂等,如果能保证加法操作只回放一次,其结果还是最终一致的。
how(如何保证最终一致性):
Counter:
counter是最简单的例子,为了说明state-based和op-based的差异,在此分别给出两种形式的描述。
Op-based counter:支持两种写操作:increment和decrement,由于加法天然满足交换律和结合律,所以非常容易实现,直接转发操作即可,但是需要注意“加法不幂等,所以同步过程中需要保证不丢不重”,如下图:

state-based counter:
counter的state-based形式并非那么的显而易见,为了简化问题,我们先从一个只有increment的counter开始看起。
G-Counter (Grow-only Counter):
由于同步的是全量,如果每个副本单独进行累加,在进行merge的时候无法知道每个副本具体累加了多少,更不能简单的取一个max作为最终结果,比如:A做一次INCR 1,同时B做一次INCR 2,副本全量同步之后,A和B都取max以2做为结果并最终一致,但正确的结果应该是3。所以一种可行的方式是在每个副本上都使用一个数组保留其它所有副本的值,update时只操作当前副本在数组中对应项即可,merge时对数组每一项求max进行合并,query时返回数组的和,即为counter的当前结果。即update和merge均能保证单调的递增,所以G-Counter是state-based CRDT。


PN-Counter:
带有decrement的state-based CRDT也并非像G-Counter那样显而易见,带有减法之后,不能满足update时单调的偏序关系。 所以正确的方式是构造两个G-Counter,一个存放increment的累加值,一个存放decrement的累加值。
Register:
register本质是一个string,仅支持一种写操作assign。并发assign是不存在交换律的,所以需要考虑附加上偏序关系。
Last-Writer-Wins Register (LWW Register)一种简单的做法是后assign的覆盖先assign的(last write wins),方式是每次修改都附带时间戳,update时通过时间戳生成偏序关系,merge时只取较大时间戳附带的结果。
Set:
Set一共有两种写操作,add和remove,多节点并发进行add和remove操作是无法满足交换律的, 会产生冲突(如下图),所以必须附加一些额外信息,可以从一个只做添加的set开始看起。

Grow-Only Set (G-Set)
set的add操作本质上是求并,天然满足交换律、结合律和幂等律, 满足Op-based CRDT:
交换律: X U Y = Y U X
结合律: (X U Y) U Z = X U (Y U Z)
幂等律: X U X = X
2P-Set
考虑删除操作,思路和PN-Counter一致,使用两个G-Set, set A只负责添加,对于从set A中remove的元素不做实际删除,只是复制到set R中,如下:

query时如果元素在set A且不在set R中,则表示该元素存在。由于只同步操作,且两个set只添加不减少,易证其为op-based CRDT。但2P-Set十分不实用,一方面已经被删除的元素不能再次被添加(原因是:R中已经存在,add多次还是删除态),一方面删除的元素还会保留在原set中,占用大量空间。
LWW-element-Set
为了解决删除元素不能再次添加的问题,可以考虑给2P-Set中A和R的每个元素加一个更新时间戳,其它操作保持不变,只要在查询的时候做如下处理:


注意:一个更优化的实现是不要R集合,而A集合中每一个元素除了维护一个更新时间戳之外,还有一个删除标志位。
Observed-Remove Set (OR-Set)
还有一种想法不太相同的设计,核心思想是每次add(e)的时候都为元素e加一个唯一的tag,remove(e)将当前节点上的所有e和对应的tag都删除,这样在remove(e)同时其它节点又有并发add(e)的情况下e是能够最终保证添加成功,此种语义称为add wins。如图,A上做remove e时仅有A一个tag,所以在C收到A同步过来的remove时,只删除tag A,tag B保留e在C上仍然存在,最终ABC三个节点是一致的,都有e及tag B。

虽然在remove时看似存在并不能保证交换律的删除操作出现,但删除的元素是全局唯一的,所以并不破坏语义,故仍然是为CRDT。
仍然有几个问题要解决:
- 重复add和remove的场景下会产生大量的tag,空间需要优化
- 在考虑空间优化的前提下如何生成全局唯一的tag
- 需要考虑如何进行垃圾回收



