trie/fsa/fst的学习
FSA（可为有序集合set）：
确定无环有限状态接收器(deterministic acyclic finite state acceptor)，即FSA。
一个FSA需要满足以下条件：
-
- 确定性的。给定输入，最多只能转移到一个状态。
- 无环的。不能反序遍历。
- 接收器。FSA可以接收一系列特定的输入。
demo:
key作为FSA的状态转移。给定一个输入key，我们可以知道这个key是否在FSA中，如下图：
如果集合中有3个key：jul、jun、mar，图如下：（FSA集合在添加jun时，其实没有新增状态节点，因为jun和jul共享了前缀ju）
如果集合为这3个key：october，november，december，图如下：（因为有相同的后缀ber，在FSA中只需要编码一次就行了）
注意：判断一个key是否存在，受限于key的长度，而不是set的大小。
构建方案：
FSA和trie的区别在于，共享后缀。因此一个FSA的空间会比trie少很多，但是构建起来却更复杂。
我们如果按照key的字典序插入的话，会好很多，还是用图片来说明
按照字典序，插入顺序mon，thurs和tues。先插入mon：
插入thurs:
因为按照字典序排序的，后面的key肯定都是大于等于thurs的，因此不会和mon有相同前缀的key插入了。则FSA中一部分被冻结“mon”会被冻结（为蓝色）。
插入tues：
此时可以确定hurs会被冻住，thurs和mon可以有相同的final state。
插入zon：
因为不会在有t开头的key出现了，另外thurs和tues有一个共同的后缀s，因此状态7和状态9被合并了
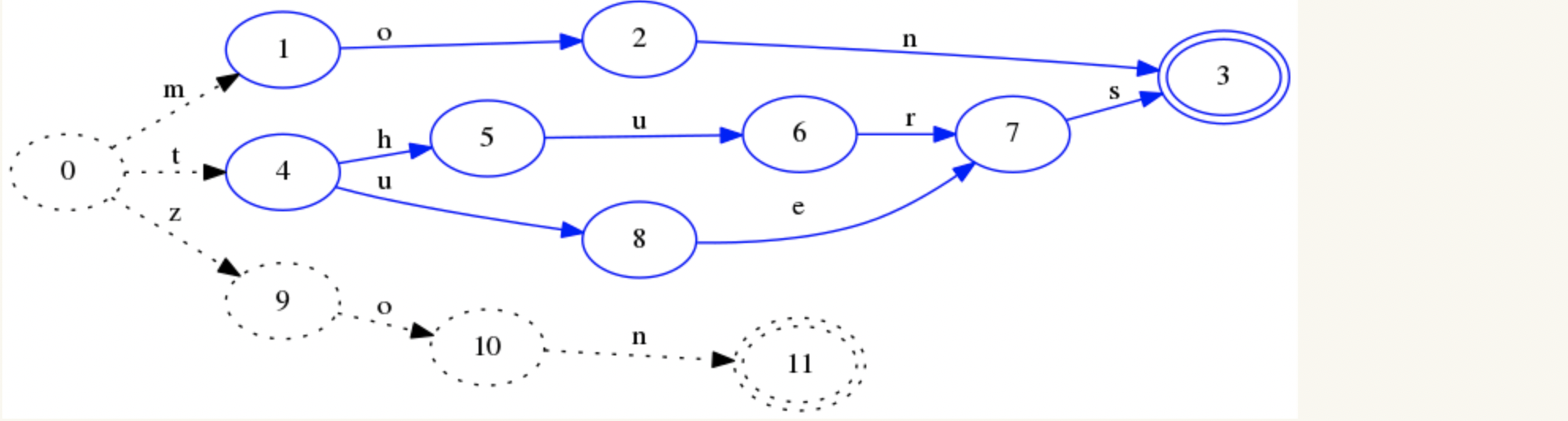
最后全部冻结：
因为mon和zon有相同的后缀，因此它们除了第一个状态转移不一样，剩下的可以重复利用。
FST（可为有序map）：
确定无环有限状态转移器，deterministic acyclic finite state transducer，即FST。
FST满足以下特性：
-
- 确定性。
- 无环。
- 一个转移器。给定一系列输入，会输出一个值。当且仅当输入会达到FST的final状态。
FST和FSA的diff：
看起来很像，但是对于一个key，FSA只回答了”yer or no”，FST不仅回答”yes or no”，还返回和这个key相关的一个值。
map的demo：
map中只包含一个数据jul，对应的value为7，表示如下图：
这和上面的集合差不多，只是在第一个转移状态j之后多了一个相关联的输出7，另外的转移u和l对应的输出都是0，所以图中就不显示了。
该map的使用：
-
- 初始化value为0
- 给定输入j,FST从状态0转移到1，value+7
- 给定输入u，FST从状态1转移到2，value+0
- 给定输入l，FST从状态2转移到3，value+0
输入结束，状态3为final状态，因此key存在，value为7。
如果map中有3个实体：jul=7,mar=3,jun=6（并且按照这个序构建map，那么建图过程如下）：
注意：在FST里用做输出的类型必须满足以下特性：
-
- 加法
- 减法
- 取前缀（对于整数来说就是min）
构建：
构建键值对 mon=2，tues-=3，thurs=5，tye=99.（注意：key按字典序列插入）
插入mon=2：
也可以如下分配：
注意：在算法上来说，把输出放在靠近初始状态的地方，代码写起来更简单。
插入thurs=5：
插入tues=3：
在把状态0-4之间的输出从5变为3的之后，需要把4之后所有的输出全部加2
插入tye=99：
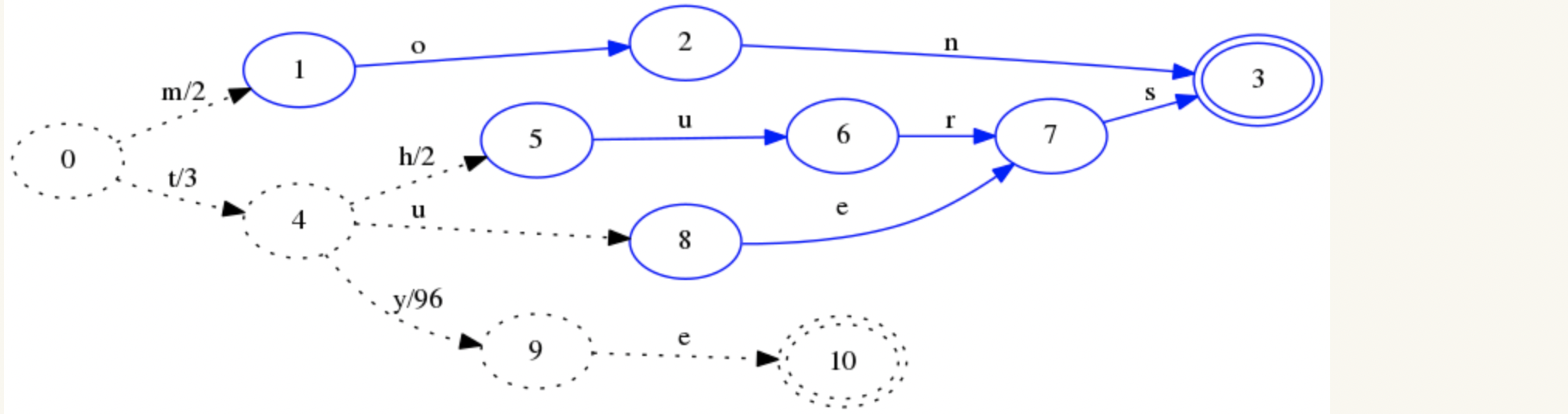
最后完成：
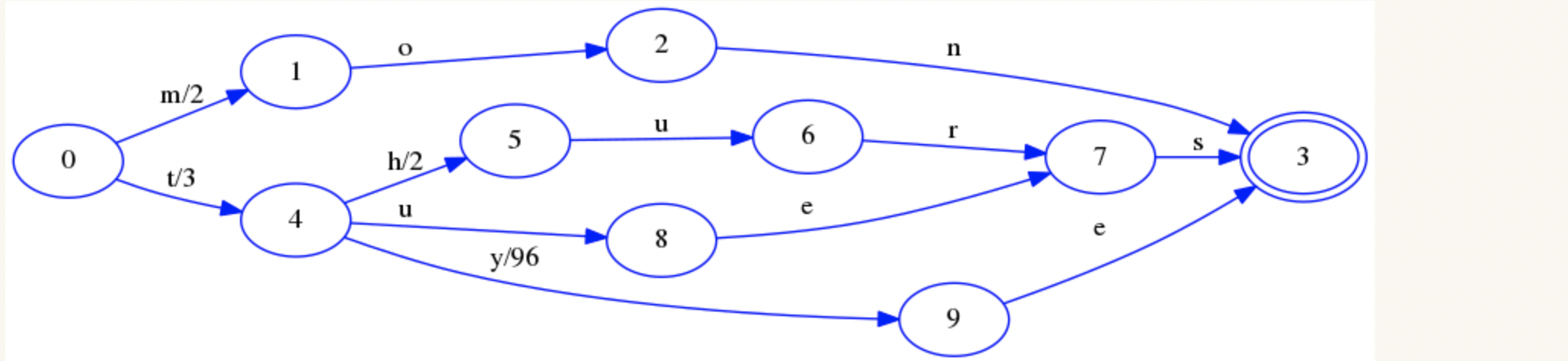
注意核心点：
值的调整：加、减、最小前缀；
值的初始化：剩下的值，优先放在前面；
建map过程：key的字典序构建；
TRIE（前缀树，trie tree）：
和FSA的区别在于，FSA可以共享前缀和后缀，而trie树只共享前缀。如键mon，tues，thus来说，FSA和trie tree如下如下图：
搜索demo：
诉求：查询Range Query从423-642。
查询点：
查找423到642之间的具体的区间：
- 423-429,640-642
- 43-49,60-63
- 5-5
