差分隐私(七):三星Harmony系列算法
动机
1、用户智能设备收集的数据对开发人员很重要
(1)智能设备(手机、家用电器、传感器、车辆)等已经成为了我们生活中的一部分
(2)它们收集到的数据对于开发人员是一笔宝贵的财富,例如三星的TouchWiz通过搜集用户自定义的界面信息来了解多模式(例如多窗口、单手模式)的使用情况并进行流行功能的改进
2、隐私问题导致数据收集面临困境
(1)用户不想让其他人知道自己的数据信息,例如浏览器历史、安装的应用程序等
(2)即使用户允许可信组织收集自己的数据,大量敏感的个人数据也会面临泄露的重大安全风险
(3)拥有庞大数据的组织面临两难境地:要么收集用户数据并面临隐私泄露危险,要么不收集这些数据并失去挖掘分析这些数据的机会
3、当时的本地差分隐私算法存在不足
(1)当时已提出的常用LDP算法各自都存在一些问题
【1】Duchi算法在特定情况无法满足差分隐私要求
【2】B & S算法在可能值量较小时效果不佳
【3】RAPPOR算法不能应用于机器学习任务
(2)其他的许多LDP算法在当时大多数处于理论阶段,而没有落实到应用上
技术细节
1、数值属性平均值估计前置算法:Duchi(算法1)
(1)客户端
【1】获取用户输入数据向量 t ,用于初始化向量 v ∈{-1,1},长度为d。其中向量 t 中的每一位 $t_{j}$ ∈ [-1,1],向量 v 初始化概率如下,$t_{j}$ 越大,$v_{j}$ 置1概率越高:
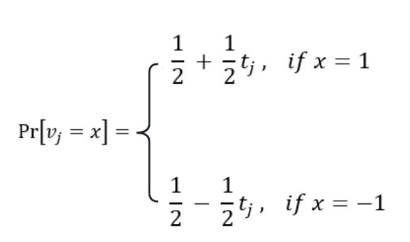
【2】使用向量长 d ,隐私预算 ϵ *计算参数B,并用于构造所有可能的加噪向量 t ∈ { -B , B}:

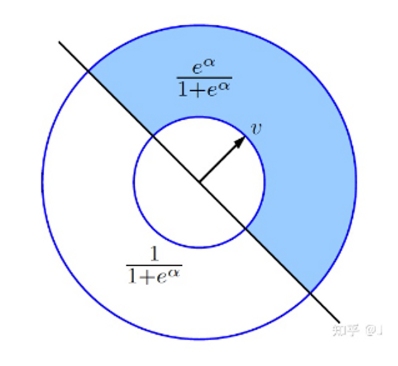
【3】将构造好的加噪向量 t* 进行划分,$T^+$中所有的向量 t* ·v > 0 (与之相对的,$T^-$中所有的向量 t* ·v ≤ 0 )
【4】生成参数 μ 满足伯努利分布(二项分布),按照一定概率置 1 。
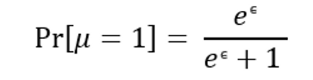
若 μ = 1 ,则从集合$T^+$ 中随机选择一个加噪向量 t* 进行输出;否则,从集合T- 中随机选择一个加噪向量 t* 进行输出。
(2)服务端
当服务端获得到所有用户发送的加噪向量 t* 后,只需要将各个用户对应的属性值累加求平均便能得到对应属性值的预估平均值。
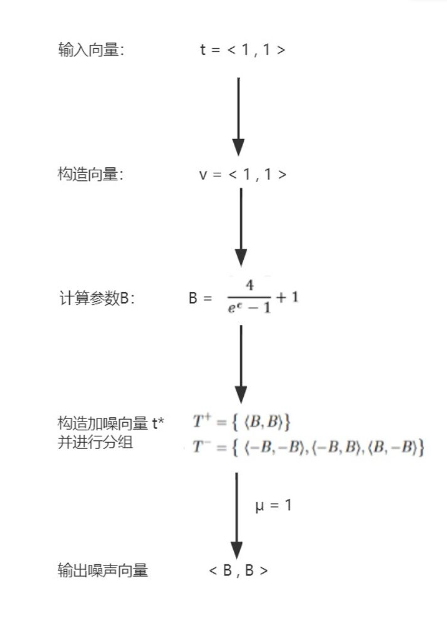
(3)问题:Duchi算法在向量长度 d 为偶数时所设置的参数 μ 概率存在问题,导致当 d 为偶数时无法满足差分隐私定义。
举例:
假设 d = 2 , 则输入向量 t1 = < 1 , 1 > , 向量 v = < 1 , 1 >
构造所有可能的加噪向量 t* ,并根据 t* · v 的结果进行分组:
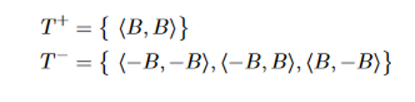
在$T^+$中,由于只存在<B , B>一种输出向量,因此选中该向量的概率为:
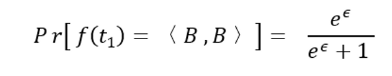
在 $T^-$ 中,由于每个加噪向量被选中的概率都是相同的,因此 $T^-$ 中每个加噪向量 t* (例:<B , -B>被选中的概率为:
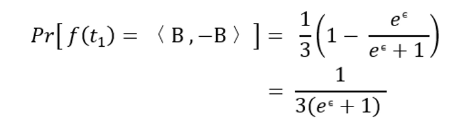
而当t2 = < -1 , -1 >时,<B , B>的分组与 t1 = < 1 , 1 > 相反,此时选中加噪向量 <B , B> 的概率为
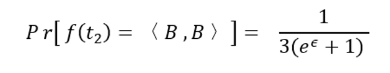
在差分隐私的定义中,两个不同的输入数据 x , x’ 经过函数 M 得到的输出结果不是固定值,而是服从一个分布。这两个输出分布的差异应小于一个阈值 ε ,即:
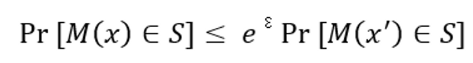
显然,当输入向量为t1 = < 1 , 1 > 和 t2 = < -1 , -1 > ,输出向量为<B , B>时,是不满足上述差分隐私的定义的,故存Duchi算法是存在问题的。
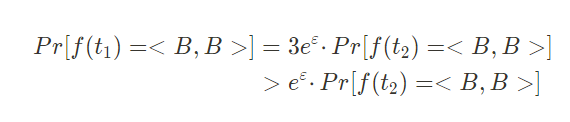
2、数值属性平均值估计算法改进(算法2)
基于Duchi算法进行改进后,新的算法能够在满足差分隐私定义的条件下实现数值属性的平均值估计。服务端的流程与Duchi相同,关键在于对于客户端的算法实施了改进:
【1】获取用户输入数据向量 t ,并初始化加噪向量 t* = < 0 , 0 … , 0 >,向量长为 d
【2】随机选择一项$t_j$ 和隐私预算 ϵ 构造出参数 μ 置 1 的概率
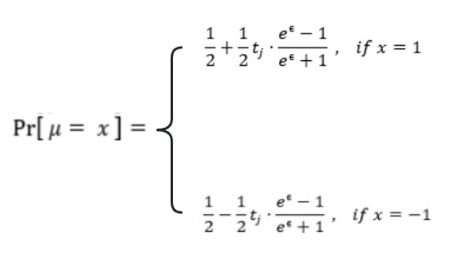
【3】根据 μ 的值选择输出结果,并放置到加噪向量 t* 中下标 j 所在的位置
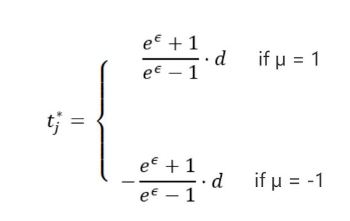

3、二元类别属性的频次估计
对于二元属性(例如 WiFi on/off) ,可以使用随机响应技术(例如Rappor算法)来进行实现。
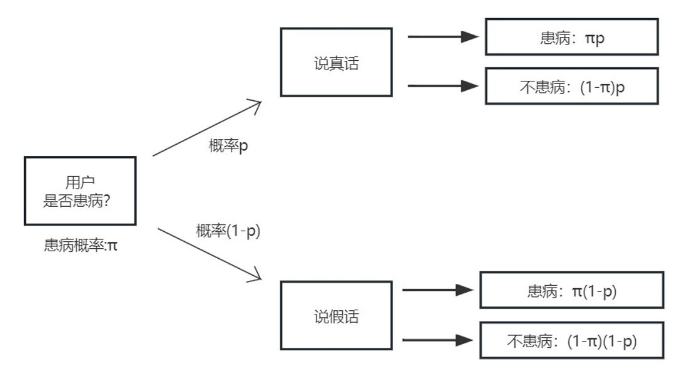
随机响应技术是一种满足差分隐私要求的频数估计算法,它的关键在于提供了一个合理的否认机制,通过该否认机制,可以模糊用户对问题的结果响应,从而实现在保护用户隐私的情况下进行频数统计的目的。
4、多元类别属性的频次估计前置算法 : B&S算法(算法3)
对于一些连续性的数值型数据会将其转换成离散的多元型类别属性(例如屏幕亮度可以离散表示成三个等级:高、中低)。
在多元属性的情况下,采用了 Bassily and Smith’s method 算法来对单个属性的各个可能值来进行频次估计。该算法假设类别属性的可能值种类数量 k 远远大于用户数量 n ,因此需要使用随机投影法来进行降维。
用于降维的矩阵Φ大小为 m × k,其中 m 是根据 k 所计算出的最优维度大小。该矩阵具有以下性质:
(1)矩阵中各列和自己进行内积的结果为 1
(2)矩阵中任意两列内积为 0
该算法的具体流程如下:
(1)客户端
【1】根据类别属性可能值种类 k 计算出最优维度大小 m
【2】根据参数 m 构造随机投影矩阵 Φ 来用于对输入向量降维,其中矩阵 Φ :
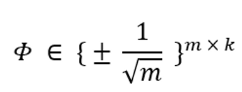
【3】随机选择一个参数 s 用作下标,代表向量的第 s 位 , s ∈ { 1 , 2 , 3 … , m }
【4】生成参数 μ 满足伯努利分布(二项分布),按照一定概率置 1
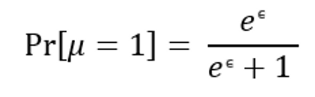
【5】根据参数 μ 的结果计算 α , 其中 $c_ϵ = \frac{e^ϵ + 1 }{e^ϵ - 1}$ ,其中 j 代表属性值$A_j$所在列:
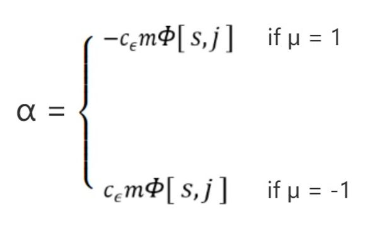
【6】将< s , α >发送到服务端,< s , α > 是指一个长度为 m 的向量 z ,在该向量中除了第 s 位值为 α 外,其他位置都为 0 。
(2)服务端
【1】服务端在收到来自所有用户的 < s , α > 后,求出它们的平均值来进行去噪:
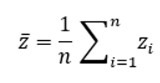
【2】通计算$\overline{x}$与$Φ_i$的内积求出每个可能值 i (1 ≤ i ≤ k)的频数估计,其中$Φ_i$投影矩阵中的第 i 列。
(3)问题:尽管Bassily and Smith’s method算法提出了一种非常好的方法来解决多元类别属性的频次统计,但依旧存在两个问题:
【1】算法所要求的的投影矩阵非常难以构造,要求过于严格,需要在 k 非常大的时候才有可能构造出。
【2】该算法在实践中的准确性不稳定,尤其是在对于 k 较小的情况下。
5、B&S算法改进
Bassily and Smith’s method算法所基于的前提是可能值数量 k 远远大于用户数量 n 的情况。因此当可能值数量 k 与用户数量相近时,可以考虑使用 k × k 大小的矩阵来进行替代,这将大幅度减小矩阵构造的难度且能够提升在 k 较小情况下算法的准确性。该矩阵的构造算法如下:
【1】计算参数 d = $2^k$ , 其中 k 代表可能值数量
【2】初始化矩阵S = {[ 1 , -1 ] , [ 1 , 1 ]} , S’ ∈ ∅
【3】设向量 v ∈ S ,遍历矩阵 S 中的向量 v 用于更新 S‘。遍历结束后用 S’ 更新矩阵 S,具体遍历规则如下:
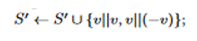
【4】判断矩阵 S 的行列式 | S |是否小于 d ,若小于则重复【3】
【5】输出矩阵 S
例子:
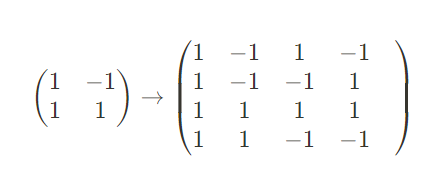
6、Harmony算法总结
给出一组属性$A_1,A_2,...,A_d$,包含数值型和类别型,Harmony给出了如下处理方案:
(1)若属性$A_j$是数值属性,则按照改进的数值型算法(小节2)来进行处理
(2)若属性$A_j$是类别型属性,则按照B&S算法(小节4&5)来进行处理
7、应用案例
1、Harmony算法在机器学习中的应用
Harmony算法可应用于多种机器学习算法中,这里以线性回归为例:
(1)简略介绍
线性回归是一种确定两个或多个变量之间依赖关系的一种方法。
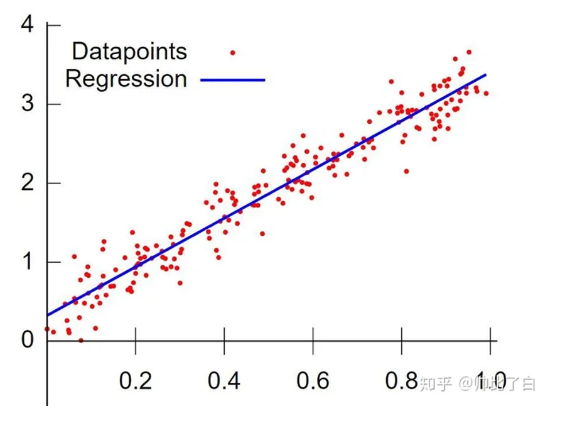
假设每个用户拥有一对数据$< x , y >$,我们需要构造一个线性函数 $y = βx + b$来对这些数据进行拟合。其中 β 代表的是线性函数的参数。 参数向量 β* 的拟合公式如下图所示:
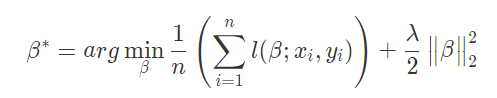
在 β* 的式子中:
第一项被称作均方误差项,用于求出能够使得理论值和实际值误差最小的参数 β ,其中函数 $l$ 被称作损失函数,用于计算出实际值和理论值的损失。
第二项被称作正则项,其作用主要是用于防止求出的参数 β 出现过拟合的现象。过拟合是指训练出的参数模型在训练集上的效果很好,但对于未知样本的预测则表现一般,是参数泛化性差的表现。
(2)梯度下降法
为了便于表达,定义:
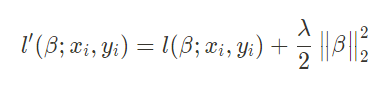
为了求出参数向量 β* 的最优解,可以采用梯度下降法来实现。
梯度下降法的核心思想是通过沿着函数的梯度方向来快速到达函数的极小值处从而获得最优解。
在梯度下降法中,参数 β 的更新方式如下:

其中 γ 表示为学习率,用于控制沿梯度方向的单步跨度
(3)Mnin-batch
在使用梯度下降法来进行参数更新时,由于使用到了Harmony算法来对上传到服务端的梯度进行加噪操作,因此若一次性使用所有数据进行训练,会导致一次性在梯度算法中加入过量噪音,降低训练结果的准确性。
为了解决这个问题,可以使用Mini-batch算法来小批次进行参数 β 的更新,每次更新使用的是该批次的平均梯度,更新方式如下,其中 |G| 代表批次:
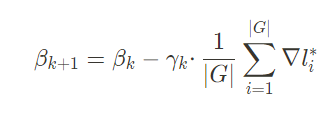
(4)算法流程
【1】获取降维向量长 r , 批次大小 g ,隐私预算 ε ,向量长 d
【2】初始化一个大小为 r × d 的投影矩阵 P ,该矩阵中每个元素被置为{ $± \frac1d$ }的概率相同
【3】初始化计数参数 k = 0 , 梯度向量 ∇ = 〈0, 0, . . . , 0〉以及学习率 γ
【4】使用 算法2 对$∇ℓ^′$ 进行加噪得到$∇^∗$进行上传,若 $∇ℓ^′$ ∉ $[-1 , 1]^r$ 则需先将该梯度投影到 $[-1 , 1]^r$ 上
【5】当梯度达到一个批次 g 数量时,对该批次梯度求平均,最后更新参数
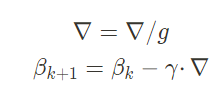
【6】重复【4】到【5】直到获得最优解进行输出

2、一种基于地理和社会属性的POIs隐私保护推荐方法框架
由于Harmony算法是一种基于其他算法所构建的复合算法,因此除了拥有较大改进的数值属性平均值估计算法外,关于类别属性频次估计相关的算法更多的是引用B & S算法。因此Harmony在实际应用中更常被用于对数值属性(例如梯度)进行处理。
近年来,基于位置的社交网络(LBSNs)技术使得用户能够通过分享观点、照片、评论等信息来和朋友于家人进行交互。Point-of-interests (POIs)兴趣点推荐技术则是通过利用用户的多模态信息(文本、图像、视频、音频等)来为用户推荐其它适合的,拥有相近信息的POI组别。
然而在这些用户信息中,常常包含在时间、位置等敏感信息,出于隐私考虑,用户一般不愿意将自己的这些数据分享给不可信的服务提供商,这给推荐质量造成了巨大的负面影响。
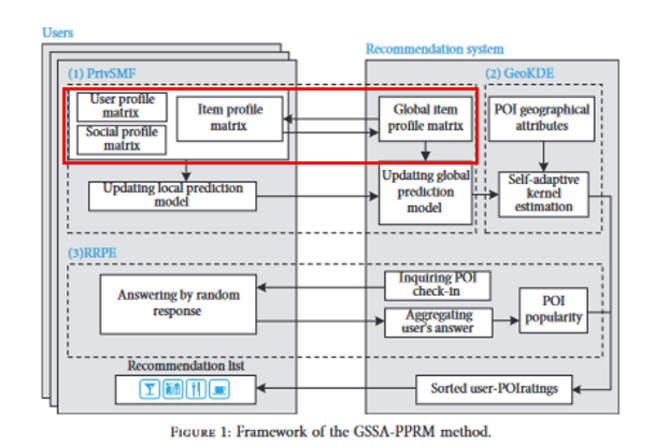
为了解决这个问题,文章提出了一个大型框架来解决这个问题。数据信息在用户端进行更新后直接在本地进行梯度训练,并将训练梯度加噪上传到服务端;服务端在收到用户梯度后求平均再分发回各个用户。该过程在框架中成为PrivSMF算法,其中加噪所使用的方法便是Harmony梯度更新算法。
8、总结
优点:
1、提出了duchi算法和B&S算法的问题,并给出了对应的改进方法
2、针对不同类型的属性数据提出了不同的解决方案,适用于多种数据类型的整合
3、能够应用于机器学习中,相比于同期其他算法实用性更强
缺点:
1、关于类别属性的频次估计算法依旧无法完全解决投影矩阵构造难的问题
2、Harmony算法所涉及的数据属性还较为单一,其他类别属性(例如集合数据类型、键值数据类型)等并没有考虑在内,有待补充


