差分隐私(六):苹果CMS/HCMS/SFP系列算法
动机
1、对用户数据的分析有助于公司改善用户的使用体验
(1)了解流行新词,加入字典方便用户输入
(2)了解受欢迎的运动,推荐给有需要的用户
2、获取用户数据可能会侵犯用户隐私,需要谨慎处理
(1)可选择加入,用户未明确同意之前不会记录和传输任何数据
(2)限制数据传输频次,每天一次
(3)无IP标识,有IP标识和多个记录关联的数据信息将被丢弃
实现细节
1、哈希函数/哈希表/哈希冲突
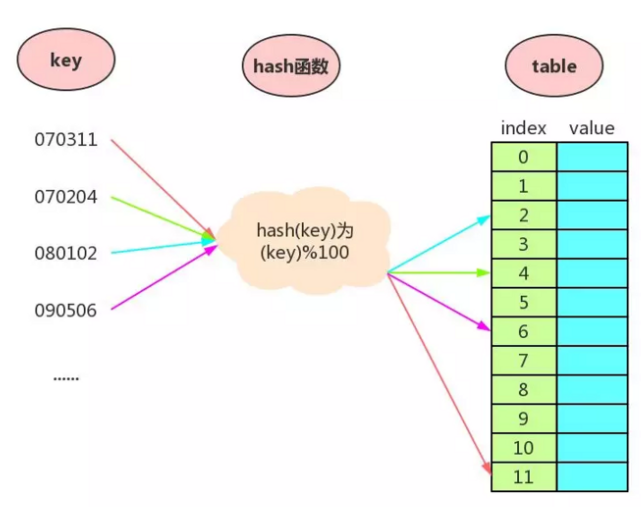
(1)哈希函数:将任意长度输入值映射到固定域来用作位置索引的函数。
(2)哈希表:根据哈希函数结果进行数据存储与访问的数据结构。
(3)哈希冲突:两个或多个不同的键值被哈希函数映射到同一个位置的情况。
2、Count Mean Sketch(CMS)算法
(1)客户端流程
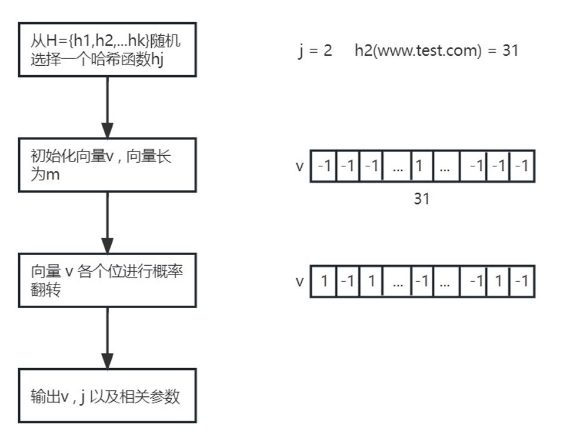
【1】从哈希函数集 H 中随机选取一个哈希函数 hj 用于对候选项进行映射,得到键值 i ,j 代表着哈希函数在H中的序号。
【2】初始化一个长度为m的向量v,除了键值 i 对应索引位置置1外,其余位置都置 -1 。
【3】将向量 v 中的每一位按照一定的概率进行翻转,通过这种方式添加随机噪声来保护用户数据隐私。
【4】将向量 v 和随机选择的hash函数序号 j 上传到服务器,同时上传的参数还有隐私参数ε,向量长 m 以及 哈希函数个数 k。
(2)服务端流程
【1】从客户端收集数据集 D = { (v1,j1) , (v2,j2) , (v3,j3) ,…, (vn,jn) },其中n代表着收集到的数据数量。同时获取隐私参数ε,向量长 m 以及 哈希函数个数 k
【2】定义并计算
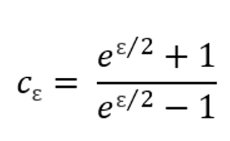
【3】计算出m维向量xi,(0<i≤ n) ,数据集更新为$D’ = { (x_1,j_1) , (x_2,j_2) , (x_3,j_3) ,…, (x_n,j_n) }$
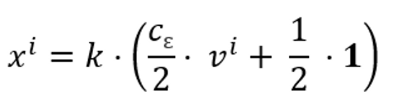
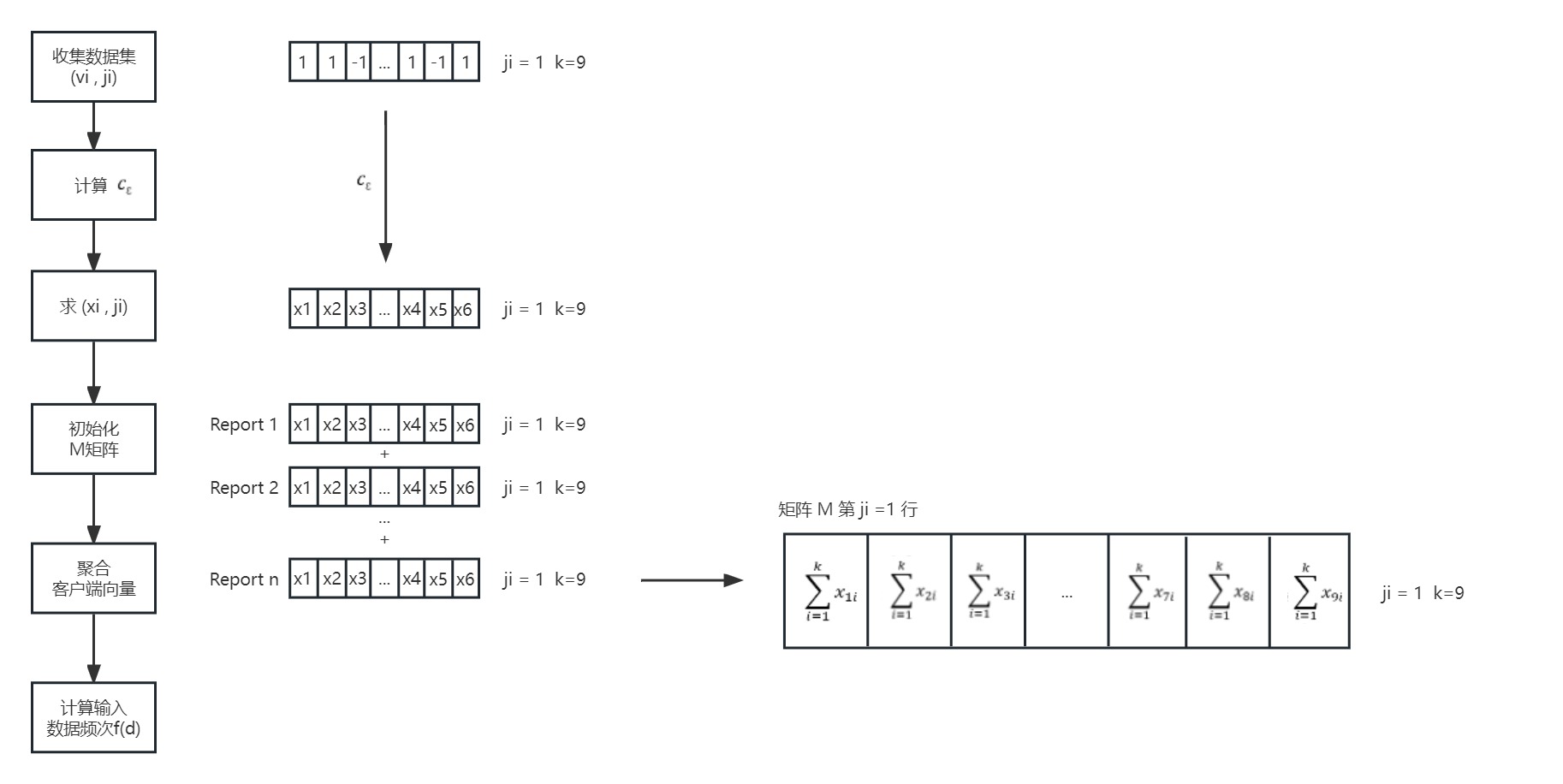
【4】构造一个k*m大小的矩阵M,并初始化全元素为0。
【5】将向量 xi(0<i≤ n)中的每位元素与矩阵M中对应第 ji 行的每位元素相加
【6】获取候选项在各行中的统计频数并求平均以及进行校正
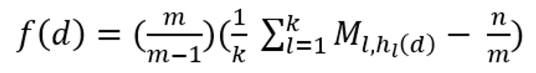
3、Hadamard Count Mean Sketch(HCMS)算法
(1)哈达玛矩阵Hm
哈达玛矩阵是一个方阵,每个元素为1或-1。初始矩阵H1 = [1] ,后续矩阵会基于以下图规律递归生成:
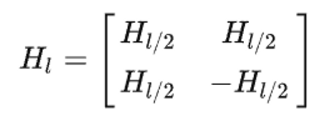
具体例子如下:
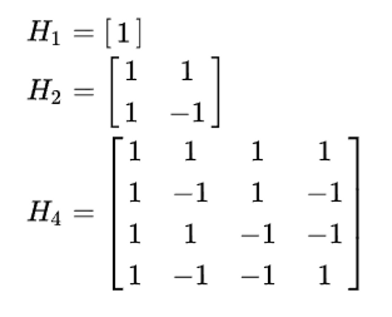
特点:
【1】哈达玛变换具有够将向量中的非零元素约束在一个更小的动态范围中的特性。通过使用哈达玛矩阵变换,矩阵中的非零元素将会被集中在边角上。

【2】矩阵可逆,在数据进行传输后可以进行还原
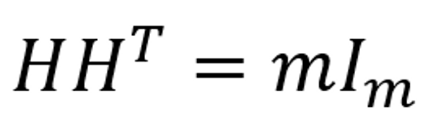
作用:
而在HCMS算法中,希望向量信息能够被压缩上传,且到达服务端后仍然能够还原出有效的信息。哈达玛矩阵对于这个目的特别有用。
(2)客户端流程
【1】从哈希函数集 H 中随机选取一个哈希函数 $h_j$ 用于对候选项进行映射,得到键值 i ,j 代表着哈希函数在H中的序号。
【2】初始化一个长度为m的向量v,除了键值 i 对应索引位置置1外,其余位置都置 0 。
【3】使用哈达玛矩阵进行变换,将向量 v 转换为向量 x。
【4】从向量 x 中随机选 选择索引 l 进行一定概率的翻转,得到值$x_l$
【6】将序号 j , 索引值L 以及值 $x_l$连同参数一同上传到服务端
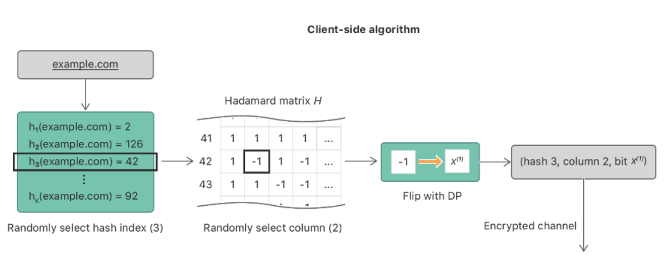
(3)服务端流程
【1】从客户端收集数据集 D =$ { ( j_1 , l_1 , x_1) , ( j_2 , l_2 , x_2 ) , ( j_3 , l_3 , x_3 ) ,…,( j_n , l_n , x_n ) }$,其中n代表着收集到的数据数量。同时获取隐私参数ε,向量长 m 以及哈希函数个数 k
【2】定义并计算
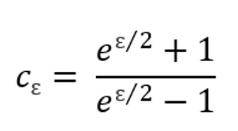
【3】计算出$y_i$,数据集更新为D‘ =$ { ( j_1 , l_1 , y_1) , ( j_2 , l_2 , y_2 ) , ( j_3 , l_3 , y_3 ) ,…,( j_n , l_n , y_n ) }$
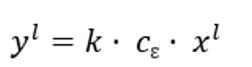
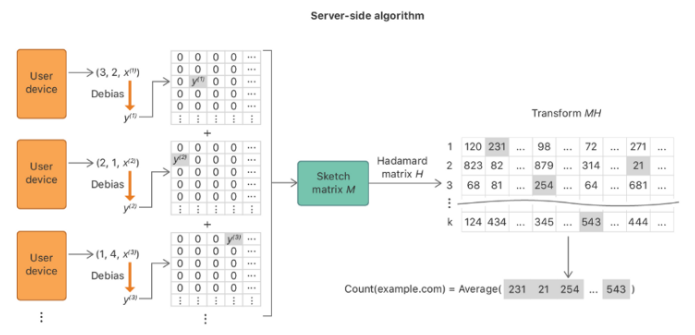
【4】构造一个k*m大小的矩阵M,并初始化全元素为0。
【5】将 yi(0<i≤ n)根据 坐标$( j_i , l_i )$在矩阵M上进行累加,并利用哈达玛矩阵的性质乘以转置哈达玛矩阵进行还原。
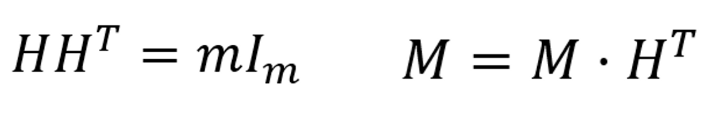
【6】获取候选项在各行中的统计频数并求平均以及进行校正。
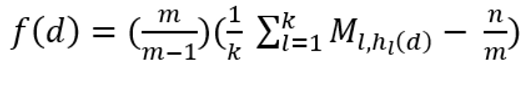
4、Sequence Fragment Puzzle(SFP)算法
(1)算法核心思想
SFP算法的核心思想是通过统计高频的字符串子片段来“构造”出未知的字符串,基于的原理是在高频出现的字符串中,其子片段也会高频出现。通过将字符串进行拆分,使得字符串的频次计算量大幅度减少。假设字符串的长度为10,字符串子片段长为2,最坏情况下需要进行的字符串遍历计算量如下,其中K代表字符串子片段映射值的数量。

(2)客户端流程
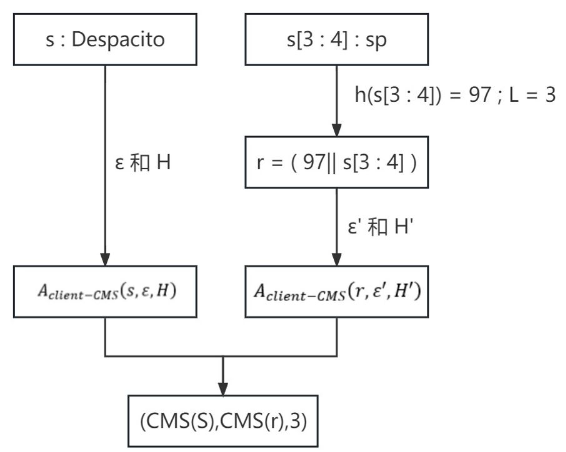
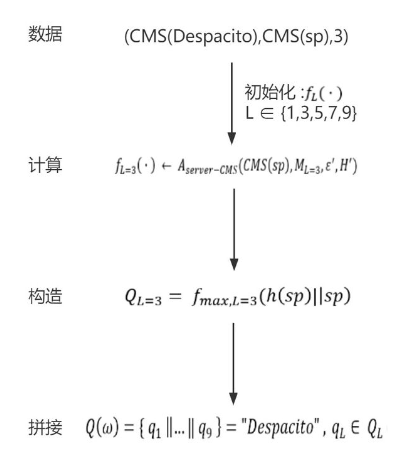
【1】设置隐私参数(ε , ε')和哈希函数集 (H ,H') 。其中 ε , H 用于完整字符串 s(例: 未知字符串Despacito) ; ε‘ , H’ 被用于字符串片段(例: sp)。另需哈希函数h用于计算片段映射。
【2】对索引 L = {1,3,5,7,9} 进行采样并构造片段 s[L : L + i] 。为了更容易说明,这里使用长度为2的子字符串,即 s[L : L+1]
【3】对构造的字符串进行哈希映射(例: 97),并进行拼接得到拼接字符串 r
【4】将完整字符串 s 和拼接字符串 r 分别进行CMS客户端算法运算,得到的结果分别为CMS(S)和CMS(r)
【5】将 (CMS(S),CMS(r),L) 作为输出结果上传到服务器。
(3)服务端流程
【1】收集来自客户端的数据,隐私参数以及哈希函数集
【2】初始化频次集合 f( · ) ,用于存储各字符串片段的频次
【3】遍历字符串片段的所有可能组合,确定搜集数据所对应的字符串片段
【4】统计字符串片段的频次,并根据片段索引将其加入频次集合 f( · )
【5】构造序列集合Q,将f( · )中每个索引上频次最高的字符串片段放入Q对应的对应序列中
【6】将Q中构造好的字符串存入字典D中,并用CMS(S)验证准确率
应用案例
(1)收集系统字典中不存在的单词
苹果通过在系统中部署SFP算法来收集字典中不存在的单词。 例如在英语中发现了多种类的新词:
【1】有缩写类的‘wyd(what are you doing’ , ‘wbu(what about you)’ ;
【2】流行表达类的’bruh(bro)’ , ‘bae(baby)’ , ‘tryna(trying to)’;
【3】还有季节性常用单词的‘Mayweather’ ,‘Despacito’ ,‘Moana’’等单词。
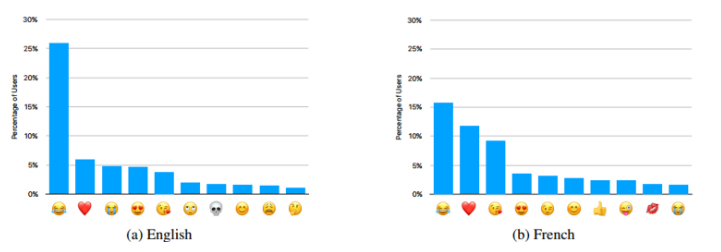
(2)表情符号使用频次
为了确定不同国家的用户最常使用哪些表情包,以及不同国家之间的差异,苹果公司使用了CMS算法来进行统计。最终可以统计到不同国家的用户最常用的表情包,通过将这些表情包放置在输入法的首选项来方便用户的输入。
(3)Safari 浏览器的自动播放策略
Safari浏览器具有自动播放某些网站的媒体元素的策略,但并非所有用户都喜欢这种自动播放策略。因此苹果公司希望能够通过分析用户的行为设置来更改系统的默认播放策略。在收集到相关的数据报告后,使用CMS算法来进行处理。通过使用CMS算法,成功识别出了一批用户热衷于开启自动播放策略的网站。例如流媒体服务网站、大型开放课程网站(MOOC)以及流行的视频网站等。
算法评价
1、CMS/HCMS算法
优点:
(1)易于实现:算法流程实现简单,易于在客户端设备和服务端设备中进行部署
(2)隐私保护:通过添加噪声的方式保障了用户的数据隐私安全
(3)可拓展性:能够处理任意长度的字符串,且可以在字典中对已知字符串进行增加
缺点:
(1)上传问题:对于CMS算法来说,上传向量可能过长,导致会存在带宽成本问题
(2)未知字符串问题:对于HCMS算法来说,尽管解决了CMS算法中上传向量过长的问题,但算法成立的基础是在知晓候选字符串的前提之上,依旧没有很好的方法来处理未知字符串。
2、SFP算法
优点:
(1)解决了如何处理未知字符串的问题
(2)通过将字符串差分成片段的方式降低了计算量
缺点:
(1)SFP算法基于CMS算法,因此同样存在上传问题
(2)对于比较复杂,或者数量较少的未知字符串,可能难以有效地进行构造


 浙公网安备 33010602011771号
浙公网安备 33010602011771号