差分隐私（四）：RAPPOR算法（随机响应&EM算法）抛硬币案例分析

随机响应技术抛硬币案例

抛硬币极大似然估计

第一步：计算出患病和不患病的概率

 

第二步：构造极大似然函数

 

第三步：求出患病人数预估结果

 

EM算法

 

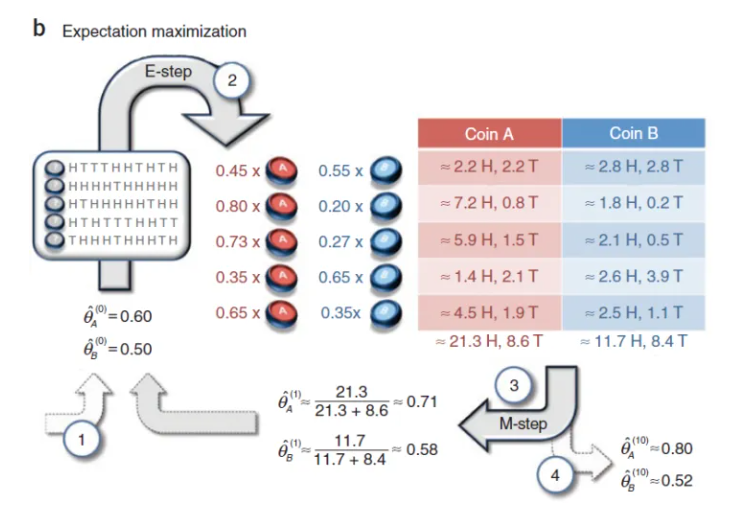
1、贝叶斯公式计算实验使用了哪个硬币

已知

硬币A正面朝上概率0.6

硬币B正面朝上概率0.5

 

设

事件A：使用A硬币进行实验

事件B：实验结果抛十次正反朝上各五次=使用A硬币进行实验 + 使用B硬币进行实验

事件C：使用B硬币进行实验

 

求

P(A|B) : 使用A硬币抛十次正反朝上各五次的概率

 

贝叶斯公式：

 

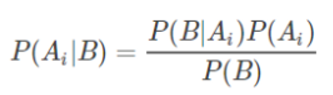
则

 

得

P(A | B) = 0.45

P(C | B) = 1 - P(A | B) = 0.55

 

2、极大似然估计

 

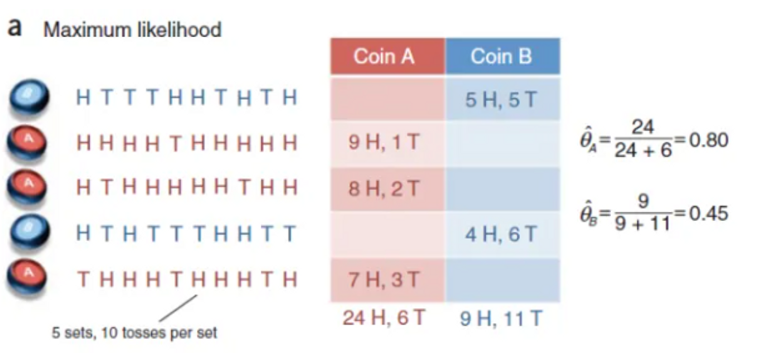
例子：已知每份样本使用的是硬币A还是硬币B，求硬币A和B正面朝上的概率。在得知了每次实验选择的硬币概率和样本结果后，需要计算使用的概率分布，通过使用极大似然估计来求得概率分布。具体流程如下：

 

步骤一：构造似然函数

步骤二：取对数整理，便于计算

步骤三：求导并取零，得到似然方差

步骤四：解似然方程，得到的结果为所求参数

 

 

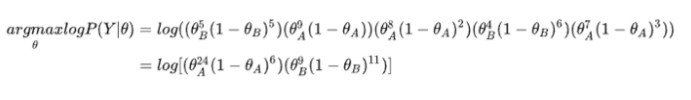
对上述式子求导后发现，5 次实验中A正面向上的次数再除以总次数作为即为θA‘，5次实验中B正面向上的次数再除以总次数作为即为θB’，即

 

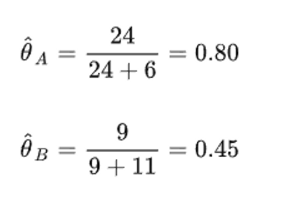
在RAPPOR算法中，同样也使用了这个技巧进行极大似然估计的运算。