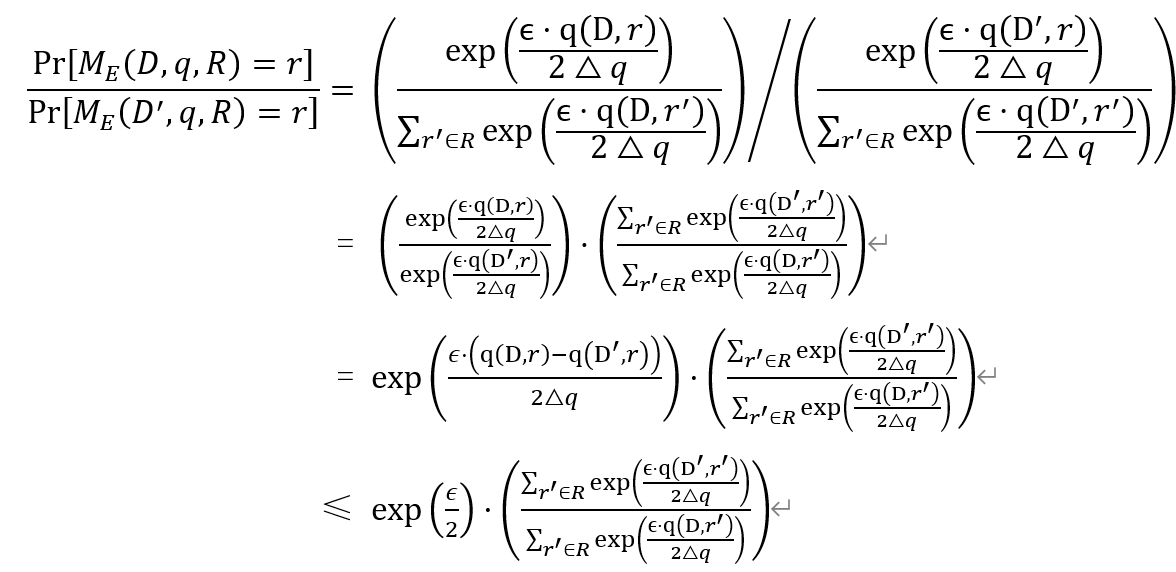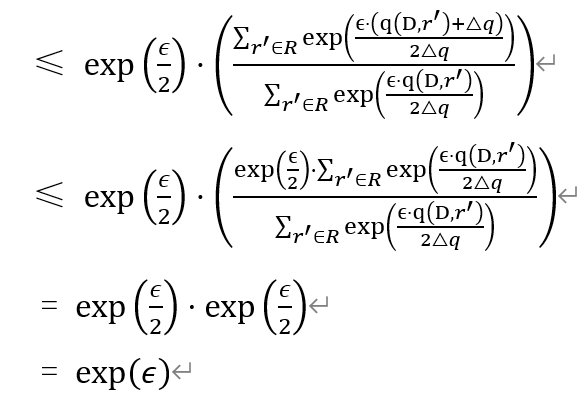差分隐私（一）：概念

一、什么是差分隐私（定义）

    差分隐私是一种保护数据隐私的方法，通过添加噪声来扰动原始数据，进而确保数据在输出时受单条记录的影响始终低于某个阈值,使得攻击者无法使用差分攻击推断出个体的敏感信息。

 

二、简单的例子

（1）差分攻击

 

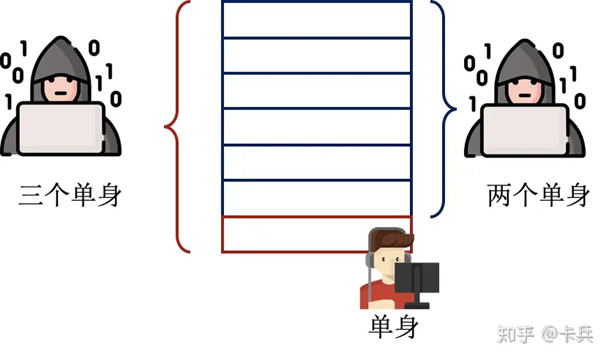
图一：差分隐私攻击

    假设现在有一个婚恋数据库，2个单身8个已婚，只能查有多少人单身。刚开始的时候查询发现，2个人单身；现在张三跑去登记了自己婚姻状况，再一查，发现3个人单身，所以张三单身。

 

（2）差分隐私

 

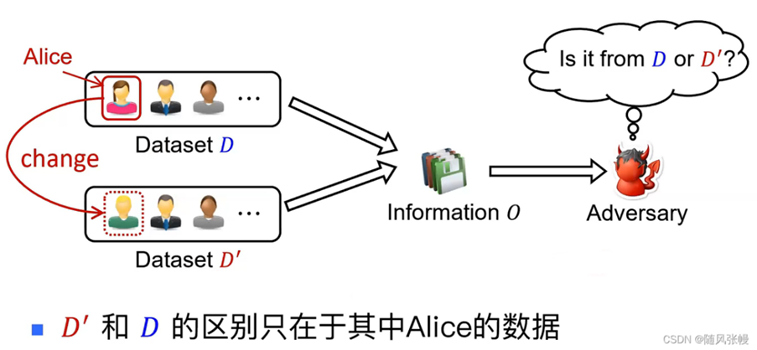
图二：差分隐私保护

    如图二所示，如果攻击者无法判别信息O是来自于D还是D'，那么我们可以认为Alice的隐私受到了保护。差分隐私应当避免让攻击者分辨出任何具体的个人数据，为此需要将被发布的信息进行一个随机算法处理，且该随机算法会对信息做一些扰动

 

三、基本理论

（1）敏感度

    敏感度是指在两个数据集(彼此之间只相差一个元素)D和D'中，一个查询函数f(·)最大的变化范围，定义为：

 

（2）KL-Divergence & MAX-Divergence

    KL-Divergence又叫做相对熵，用于衡量两个概率分布之间的不同程度，离散随机变量相对熵的公式如下：

 

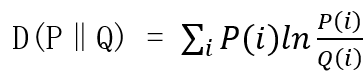
    但我们关注的并不是两个分布的整体差异，而只需要求出两个分布之间的最大差异，因此引入了MAX-Divergence，并且需要它小于ε：

 

    将不等式进行化简，用e指数运算将ln符号消去，并移动分母，将离散型变量替换成查询结果M,最终得到式子：

 

    其中M(x) = f(x)  + r， 代表查询函数，r代表随机噪声，M(x)代表最终的查询结果，S代表该查询结果的可能取值范围。

 

 

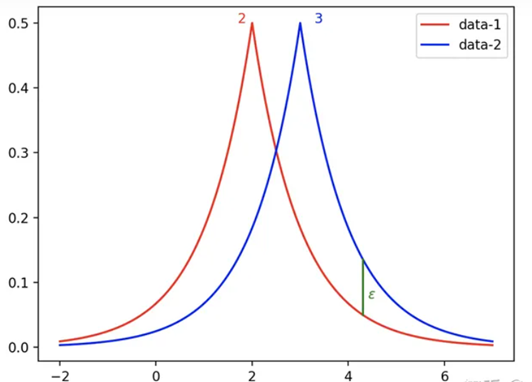
（3）松弛

    在拉普拉斯机制的定义中，差分隐私过于严格导致了可用性的下降，而实际应用中需要更多的隐私预算，因此为了算法的实用性，后续又引入了松弛版本的差分隐私，即：

 

    其中δ作为松弛项，代表一个可以容忍的较小差距，一般设置得比较小。

 

 

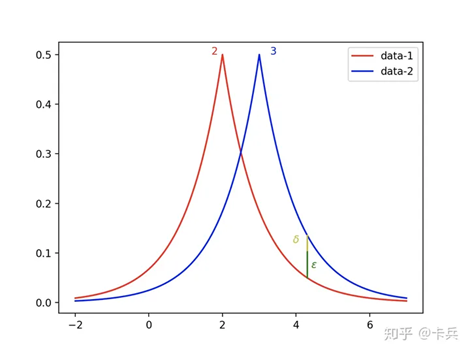
    如图，按照严格的差分隐私机制来讲，是不满要求的。但考虑到松弛项 后便依旧能够满足差分隐私的条件。

 

四、拉普拉斯机制

（1）拉普拉斯分布

 

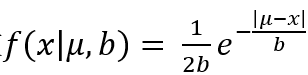
    该分布叫做拉普拉斯分布，其中μ代表位置参数，b代表尺度参数。记作Laplace(μ,b)

 

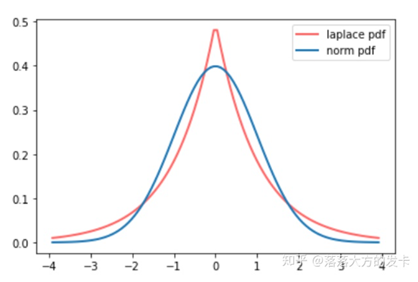
当b=1时，拉普拉斯分布与标准正态分布的对比

    使用拉普拉斯分布的原因：

　　【1】拉普拉斯分布是对称的，均值为零，具有良好的加性噪声特性。当在数据中添加拉普拉斯噪声时，整体的数据分布特性不会发生剧烈变化，从而在保证隐私的同时，仍能保持数据的实用性。

　　【2】拉普拉斯分布具有长尾性，其概率密度函数在远离均值的位置衰减较快，这意味着在添加噪声时，极端值的影响会被迅速削弱，精度更高。

 

（2）拉普拉斯机制

M(D) =  + Y(Y₁,Y₂…,Y_k)

    其中M(D)代表输出的结果，D为数据集， 代表的是真实的查询结果，Y代表着噪声。这里使用的是拉普拉斯分布Y-L(0, ),其中 代表前文提及的敏感度， 代表隐私预算。隐私预算 用于衡量隐私保护的程度，隐私预算越小，噪声越大，结果可用性越小，隐私保护越好。

 

    因此，我们最终需要满足的公式证明如下

 

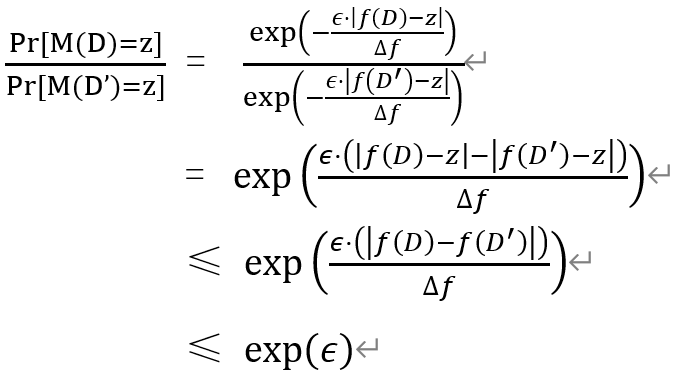
    其中，第二行等号是第一个式子化简得到；第三行不等号利用了绝对值三角不等式；第四行不等式用的是上面讲的敏感度定义。

    拉普拉斯机制适用于计数查询以及直方图查询。

 

五、高斯机制

    拉普拉斯机制提供的是严格的差分隐私机制，而高斯机制提供的则是松弛的差分隐私机制，式子如下：

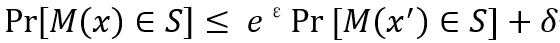
    其中 ∈(0,1), M(x) =  + Y(Y1,Y2…,Yk),噪声使用的是高斯分布Y-N(0,σ²)。高斯分布的标准差σ决定了噪声的尺度，ε表示隐私预算，δ表示松弛项。

    因此，在高斯分布中，输出可以被分成两部分，第一部分是严格遵守差分隐私的部分，第二部分是违反了严格差分隐私的部分

    其中第一部分，令

 

 

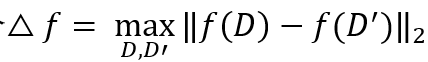
则需要满足的公式如下：

 

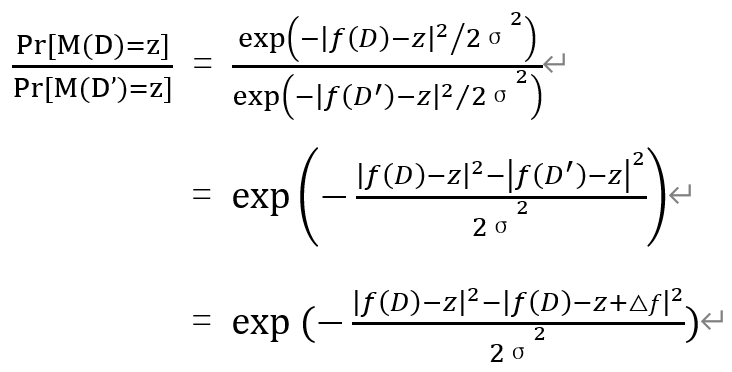
    令x = f(D) - z   ,由于概率恒正，则：

 

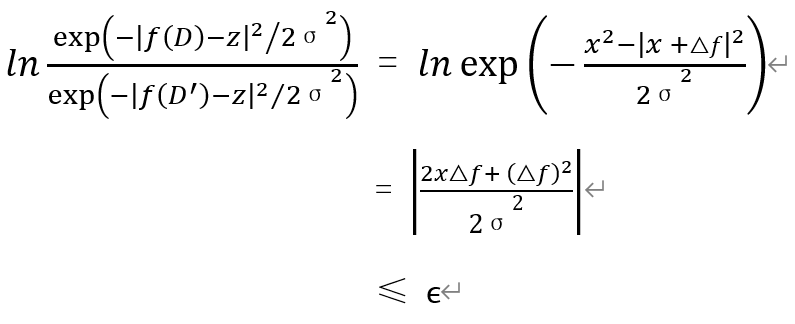
         综合来说，结合两部分的最终输出证明如下：

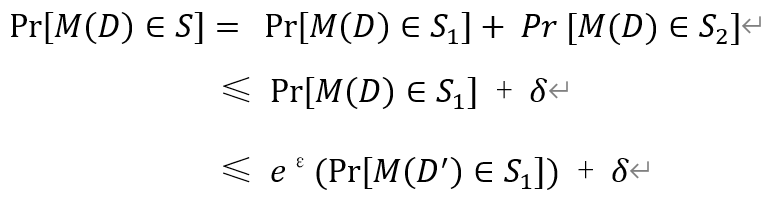
　　使用高斯分布的优势：

　　【1】高斯分布具有更强的集中性，大部分概率质量集中在均值附近。这种性质使得它在实践中能够在同样的隐私预算下，提供更小的误差，从而提高查询结果的准确性和可用性。

 

六、指数机制

    与前两种机制不同，前面两种都是简单地对输出的数值结果加入噪声实现差分隐私。而对于非数值型数据而言，它的输出是一组离散数据{R₁,R₂,…,R_N}中的元素。

    指数机制整体的思想就是，当接收到一个查询之后，不是确定性的输出一个R_i结果，而是以一定的概率值返回结果，从而实现差分隐私。而这个概率值则是由打分函数确定，得分高的输出概率高，得分低的输出概率低。

（1）敏感度

    由于和前面的数值型数据不同，因此需要对敏感度进行重新设定:

  

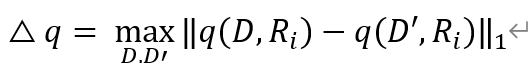
    其中D代表数据集， 代表某一个输出结果R_i的分数。

 

（2）指数机制

    在指数机制中，是以${ \mathrm{M}\left(\mathrm{D}, \mathrm{q}, \mathrm{R}_{\mathrm{i}}\right)-\exp \left(\frac{\epsilon \cdot \mathrm{q}\left(\mathrm{D}, R_i\right)}{2 \Delta q}\right) }$的概率输出结果R_i。但是${ \exp \left(\frac{\epsilon \cdot \mathrm{q}\left(\mathrm{D}, R_i\right)}{2 \Delta q}\right) }$表示的不是概率值，因此需要进行归一化以得到对应的概率值。

 

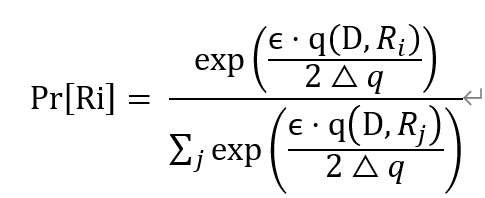
因此，指数机制需要满足的公式证明如下：