3D数学基础：图形和游戏开发（第2版） 第二章 笔记

3D数学基础：图形和游戏开发（第2版） 第二章 笔记

供参考和备忘用

向量（Vector）

对数学家来说向量就是一个数字列表，对程序员来说向量可以数组（Array）表示，但在计算机的图形开发中我们侧重于向量的几何表示。

从几何学上讲，向量是具有大小和方向的有向线段。在图形上常用箭头（起点指向终点）表示，因为它捕获了向量的两个定义特征：大小和方向。

• 向量的大小（Magnitude）：是指向量的长度。向量的长度是非负的。
• 向量的方向（Direction）：是指向量在空间中指向的方向。

向量是没有位置的，只有大小和方向。它描述了从一个位置到另一个位置的位移，是一种相对位置关系而不是绝对位置。

向量a可书写为：\(\vec a\)

在纸面上描述向量

在书写向量时，有两种表达方式：水平写入和垂直写入，水平写入的向量称为行向量（Row Vector）,垂直写入的称为列向量（Column Vector）。

行向量

如下所示的一个三维行向量，各个数字间可用逗号或空格隔开：

\[\begin{bmatrix} x,y,z \end{bmatrix} \]

列向量

如下所示的一个三维列向量：

\[\begin{bmatrix} x\\ y \\ z \\ \end{bmatrix} \]

向量的维度

向量的维度表示向量中元素的个数。一个元素就是一维向量，两个数元素就是二维向量，三个元素就是三维向量......

分量

分量用来表示向量中具体的某一个元素，比如向量中的第一个分量表示向量中的第一个元素。
表示方式：

1. 使用下标，如：\(v_1\) 指的是向量 \(v\) 中的第一个元素。
2. 使用字母，使用x、y来指代二维向量中的元素；使用x、y、z表示三维向量中的元素；使用x、y、z、w表示四维向量中的元素。

例如，如下向量中，\(a_1 = a_x = 1\)表示的都是向量 \(a\) 的第一个分量。

\[a = \begin{bmatrix} 1 \\ 2 \\ \end{bmatrix} \]

标量（Scalar）

标量其实就是普通数字的技术术语，与我们日常中使用的数字无异。

使用笛卡尔坐标指定向量

在二维笛卡尔坐标中，X向右为正，Y向上为正。对于二维向量\([1.5,2]\)，在二维笛卡尔坐标系中可描述为：向右移动1.5个单位然后向上移动两个单位，或者向上移动两个单位然后向右移动1.5个单位。

零向量（Zero Vector）

零向量表示没有方向且长度为0的向量。可以将零向量看作是表达“无位移”概念的一种方式。

向量与点

点用于指定位置，向量用于描述位移。

点的位置是相对的——相对于指定其坐标的坐标系的原点。

向量描述了一个位置到另一个位置的位移，是一种相对位置关系。

所以，如果从原点（参考点）开始并按向量\([x,y]\)指定的量移动，那么将最终到达点\((x,y)\)所描述的位置。也就是说向量\([x,y]\)给出了从原点（参考点）到点(x,y)的位移。比如，在二维笛卡尔坐标系中，点：\((1,2)\)，可以表示为向量：\([1,2]\)，原点(0,0)开始，向右移动了1个单位，然后向上移动了2个单位，然后到达点\((1,2)\)。

一切都是相对的

世界上有很多东西都是很难建立“绝对”参考的东西。比如上面提到的点和向量。另外还有温度、速度、音量等等。
比如我们说体温是：37.3℃，是相对于0℃（水的冰点）来说的。

向量的运算

负向量

负向量就是将向量的每一个分量变为其相反数。\(\vec a\)的负向量为\(-\vec a\)

比如，向量：\([-3,2]\)的负向量为：\(-[-3,2] = [3,-2]\)

使向量变负会产生大小相同但方向相反的向量。

向量与标量的乘法

被乘数与乘数

被乘数一般放在算式的前面，乘数一般放在算式的后面。被乘数表示需重复相加的数，乘数表示需重复相加的次数。

如：\(4 \times 2 = 8\)，4是被乘数，2是乘数。读作：4 乘以 2 等于8，或者读作：2 乘 4 等于8。表示2个4相加。

向量乘以标量

向量不能与标量相加，但是可以将向量乘以标量。其实，向量乘以标量也可以看成标量个向量相加的和。

其结果是一个与原始向量平行的向量，但具有不同的长度和可能相反的方向。也可理解为：对原始向量进行长度为标量的绝对值的缩放，如果标量小于0，则翻转向量的方向。

计算方式：将标量与每一个向量的分量相乘。如：

\[\begin{bmatrix} x \\ y \\ z\\ \end{bmatrix}k = k \begin{bmatrix} x \\ y \\ z\\ \end{bmatrix} = \begin{bmatrix} kx \\ ky \\ kz\\ \end{bmatrix} \]

向量除以非零标量

等价于向量乘以此标量的倒数。反过来，标量是不可以除以向量的。向量也不可以除以另一个向量。

\[\frac{\vec v}{k} = \vec {v}{\frac{1}{k}} \]

一些注意事项：

• 当将向量乘以标量时，不必使用任何乘法符号。乘法是通过将两个量并排放置（通常右边是向量）来表示的。
• 标量和向量的乘法和除法都在任何加法和减法之前发生。
• 负向量可以被视为将向量乘以标量-1的特殊情况。

向量的加法和减法

两个向量相加或相减，它们必须具有相同的维度，不同维度不能相加减。

向量的加法

计算方式：将向量对应的分量相加即可。如：

\[\begin{bmatrix} x \\ y \\ z \\ \end{bmatrix} + \begin{bmatrix} a \\ b \\ c \\ \end{bmatrix} = \begin{bmatrix} a \\ b \\ c \\ \end{bmatrix} + \begin{bmatrix} x \\ y \\ z \\ \end{bmatrix} = \begin{bmatrix} x+a \\ y+b \\ z+c \\ \end{bmatrix} \]

向量的加法满足交换律，即：\(\vec a + \vec b = \vec b + \vec a\)

向量的减法

相应的分量相减即可。向量的减法可以理解为加上一个向量的负向量。即：\(\vec a - \vec b = \vec a + (- \vec b)\)。如：

\[\begin{bmatrix} x \\ y \\ z \end{bmatrix} - \begin{bmatrix} a \\ b \\ c \end{bmatrix} = \begin{bmatrix} x \\ y \\ z \end{bmatrix} + (- \begin{bmatrix} a \\ b \\ c \end{bmatrix}) = \begin{bmatrix} x-a \\ y-b \\ z-c \\ \end{bmatrix} \]

向量的减法不满足交换律，即：\(\vec a - \vec b \neq \vec b - \vec a\)，它们的结果长度相同但方向相反，所以，\(\vec a - \vec b = -(\vec b - \vec a)\)。

几何解释

\[\begin{bmatrix} 1 \\ 2 \end{bmatrix} + \begin{bmatrix} 3 \\ 4 \end{bmatrix} = \begin{bmatrix} 4 \\ 6 \end{bmatrix} \]

如上所示的向量加法，可描述为：向右移动1个单位 -> 向上移动2个单位 -> 再向右移动3个单位 -> 在向上移动4个单位。

向量的大小

向量的大小也称为向量的长度（Length）。它的值是非负的。

表示方式：\(||向量||\)。如，\(\vec a\)的长度表示为：\(||\vec a||\)。

计算方式：向量各个分量的平方和的平方根。如，\(\vec v = [3,4]\)的长度计算方式为：

\[||\vec v|| = \sqrt{3^2+4^2} = 5 \]

单位向量（Unit Vector）

对于许多向量，我们只关注其方向而不是大小（如：法线（Normal）），在这些情况下，使用单位向量通常会很方便。

单位向量是大小为1的向量。单位向量也被称为归一化向量（Normalized Vector）。

任何非零向量的单位向量的计算方式：向量除以向量的长度，如下所示：

\[\hat v = \frac{\vec v}{||\vec v||} \]

例如，向量\([3,4]\)的单位向量为：

\[\frac{[3,4]}{||[3,4]||} = \frac{[3,4]}{\sqrt{3^2+4^2}} = \frac{[3,4]}{5} = [\frac{3}{5},\frac{4}{5}] = [0.6,0.8] \]

距离公式

距离为两点之间的线段长度。由于向量是有向线段，因此几何上有意义的是，两点之间的距离将等于从一点到另一点的向量的长度。

求\(\vec a\)到\(\vec b\)间距离的计算方式：

1. 第一步：求出\(\vec a\)到\(\vec b\)的向量
2. 第二步：求出该向量的长度

例如，\(\vec a = [x,y]\)，\(\vec b = [m,n]\)。求\(\vec a\)到\(\vec b\)的距离：

设，\(\vec d\)为\(\vec a\)到\(\vec b\)的向量；则，\(\vec d = \vec b - \vec a\)
计算出：\(\vec d = [m-x,n-y]\)
所以距离为：\(||\vec d|| = \sqrt{(m-x)^2 + (n-y)^2}\)

其实，计算两个向量的距离就是计算两个向量的差所得向量的长度。

向量点积（Dot Product）

点积也称为内积（Inner Product），点积的名称来自向量乘积表示法中使用的点符号，且不能省略点符号。

向量\(\vec a\)与向量\(\vec b\)的点积表示为：\(\vec a \cdot \vec b\)

计算方式：相应分量的乘积之和，得到的是一个标量。如下所示：

\[\begin{bmatrix} a_1 \\ a_2 \\ \vdots \\ a_{n-1} \\ a_n \end{bmatrix} \cdot \begin{bmatrix} b_1 \\ b_2 \\ \vdots \\ b_{n-1} \\ b_n \end{bmatrix} = a_1b_1 + a_2b_2 + \cdots + a_{n-1}b_{b-1} + a_nb_n \]

点积满足交换律，也就是说：\(\vec a \cdot \vec b = \vec b \cdot \vec a\)

这里有一个与之比较贴近现实的例子：
假设你有3吨小麦、4吨糖、2吨大米，则可以表示为：\([3,4,2]\)。
其中，1吨小麦162元，1吨糖558元，1吨大米495元，则可以表示为：\([162,558,495]\)。
那么，你的总收入为：\(3 \times 162 + 4 \times 558 + 2 \times 495 = 3798\)元。
来源：https://www.quora.com/Why-is-the-definition-of-the-dot-product-the-way-it-is

几何意义

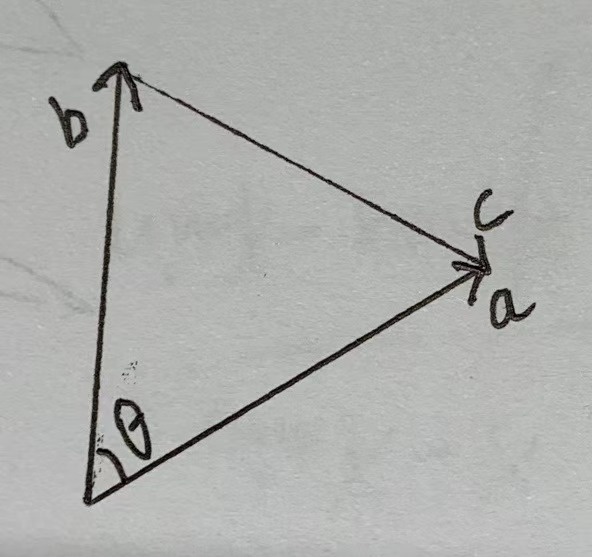
如何上图所示，\(\vec a\)与\(\vec b\)的夹角为\(\theta\)，\(\vec c = \vec a - \vec b\)，\(\vec a\)、\(\vec b\)、\(\vec c\)构成一个三角形。

由三角形余弦定理可知：

\[||\vec c||^2 = ||\vec a||^2 + ||\vec b||^2 -2||\vec a||||\vec b||cos\theta \]

假设：

\[\vec a = \begin{bmatrix} a_1 \\ a_2 \\ \end{bmatrix} \]

\[\vec b = \begin{bmatrix} b_1 \\ b_2 \\ \end{bmatrix} \]

由上方的 向量的大小 描述可知：

\[||\vec a||^2 = {a_1}^2 + {a_2}^2 \]

\[||\vec b||^2 = {b_1}^2 + {b_2}^2 \]

又：

\[||\vec c||^2 = ||(\vec a - \vec b)||^2 = ||\begin{bmatrix} a_1-b_1 \\ a_2-b_2 \\ \end{bmatrix}||^2 = (a_1-b_1)^2 + (a_2-b_2)^2 = {a_1}^2 +{b_1}^2 -2a_1b_1 + {a_2}^2 +{b_2}^2 -2a_2b_2 \]

所以：

\[{a_1}^2 +{b_1}^2 -2a_1b_1 + {a_2}^2 +{b_2}^2 -2a_2b_2 = {a_1}^2 + {a_2}^2 + {b_1}^2 + {b_2}^2 -2||\vec a||||\vec b||cos\theta \]

化简得：

\[a_1b_1 + a_2b_2 = ||\vec a||||\vec b||cos\theta \]

所以我们可以推导出向量点积的另一种计算方式：\(||\vec a||||\vec b||cos\theta\)，也就是说：

\[\vec a \cdot \vec b = \begin{bmatrix} a_1 \\ a_2 \\ \vdots \\ a_{n-1} \\ a_n \end{bmatrix} \cdot \begin{bmatrix} b_1 \\ b_2 \\ \vdots \\ b_{n-1} \\ b_n \end{bmatrix} = a_1b_1 + a_2b_2 + \cdots + a_{n-1}b_{b-1} + a_nb_n = ||\vec a||||\vec b||cos\theta \]

\(||\vec b||cos\theta\)的另一层含义是什么？

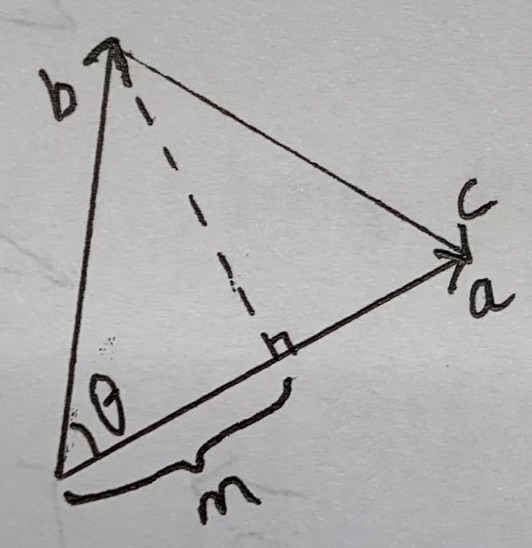
由上图和三角函数可知：\(m = ||\vec b||cos\theta\)，所以：\(\vec a \cdot \vec b = ||\vec a||m\)

那么，\(m\)是什么？\(m\)是\(\vec b\)在\(\vec a\)上投影的长度。如下图所示：

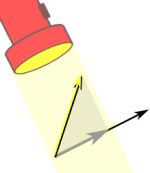
图源：https://www.shuxuele.com/algebra/vectors-dot-product.html

所以两个向量点积的几何意义为：一个向量在另一个向量上投影的长度与另一个向量长度的乘积。

两个向量夹角的启示

\(\vec a \cdot \vec b\)	\(\theta\)	角度为	\(\vec a\)和\(\vec b\)是
>0	\(0^\circ \leq \theta < 90^\circ\)	锐角	主要指向同一方向
0	\(\theta = 90^\circ\)	直角	垂直
<0	\(90^\circ < \theta \leq 180^\circ\)	钝角	主要指向反方向

向量点积的分配律

\[\vec a \cdot (\vec b + \vec c) = \vec a \cdot \vec b + \vec a \cdot \vec c \]

几何上证明：

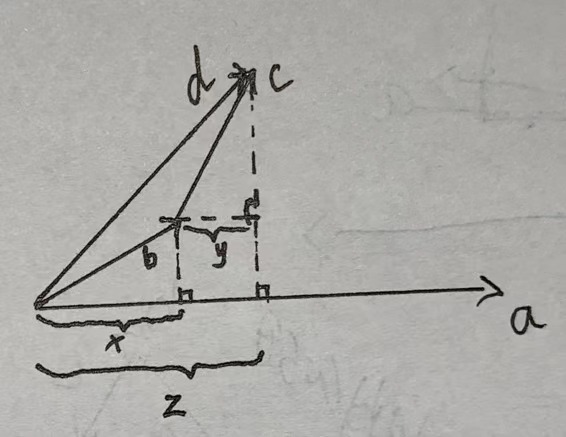
由上图所示：\(\vec d = \vec b + \vec c\)，\(\vec b\)在\(\vec a\)向量上的投影长度为\(x\)，\(\vec c\)在\(\vec a\)向量上的投影长度为\(y\)，\(\vec d\)在\(\vec a\)向量上的投影长度为\(z\)，\(z = x+y\)。
可知：

\[\vec a \cdot (\vec b + \vec c) = \vec a \cdot \vec d = ||\vec a||z \]

\[\vec a \cdot \vec b + \vec a \cdot \vec c = \vec a \cdot \vec d = ||\vec a||x + ||\vec a||y = ||\vec a||(x+y) \]

又，\(z = x+y\)，所以：

\[\vec a \cdot (\vec b + \vec c) = \vec a \cdot \vec b + \vec a \cdot \vec c \]

点积与任意矢量和标量的乘法的结合律

\[(k\vec a) \cdot \vec b = k(\vec a \cdot \vec b) = \vec a \cdot (k\vec b) \]

证明：

\[(k\vec a) \cdot \vec b = \begin{bmatrix} ka_1 \\ ka_2 \end{bmatrix} \cdot \begin{bmatrix} b_1 \\ b_2 \end{bmatrix} = ka_1b_1 + ka_2b_2 = k(a_1b_1 + a_2b_2) \]

\[k(\vec a \cdot \vec b) = k(\begin{bmatrix} a_1 \\ a_2 \end{bmatrix} \cdot \begin{bmatrix} b_1 \\ b_2 \end{bmatrix}) = k(a_1b_1 + a_2b_2) \]

\[\vec a \cdot k(\vec b) = \begin{bmatrix} a_1 \\ a_2 \end{bmatrix} \cdot \begin{bmatrix} kb_1 \\ kb_2 \end{bmatrix} = a_1kb_1 + a_2kb_2 = k(a_1b_1 + a_2b_2) \]

关于向量点积的一些参考链接：
https://www.shuxuele.com/algebra/vectors-dot-product.html
https://www.quora.com/Why-is-the-definition-of-the-dot-product-the-way-it-is

另，3Blue1Brown关于点积的笔记

向量叉积（Cross Product）

叉积又叫外积或向量积（Vector Product）,只能在三维中应用。结果是一个向量

向量\(\vec a\)与向量\(\vec b\)的叉积表示为：\(\vec a \times \vec b\)

计算方式：

\[\begin{bmatrix} x_1 \\ y_1 \\ z_1 \\ \end{bmatrix} \times\ \begin{bmatrix} x_2 \\ y_2 \\ z_2 \\ \end{bmatrix} = \begin{bmatrix} y_1z_2 - z_1y_2 \\ z_1x_2 - x_1z_2 \\ x_1y_2 - y_1x_2 \\ \end{bmatrix} \]

向量的叉积不满足交换律：\(\vec a \times \vec b \neq \vec b \times \vec a = -(\vec b \times \vec a)\)

向量的叉积不满足结合律：\((\vec a \times \vec b) \times \vec c \neq \vec a \times (\vec b \times \vec c)\)

几何意义

假设\(\vec a\)和\(\vec b\)的叉积为：\(\vec m\)，也就是说：

\[\vec a = \begin{bmatrix} x_1 \\ y_1 \\ z_1 \\ \end{bmatrix} \]

\[\vec a = \begin{bmatrix} x_2 \\ y_3 \\ z_2 \\ \end{bmatrix} \]

\[\vec m = \begin{bmatrix} y_1z_2 - z_1y_2 \\ z_1x_2 - x_1z_2 \\ x_1y_2 - y_1x_2 \\ \end{bmatrix} \]

那么计算向量\(\vec m\)的长度的平方，\(||\vec m||^2\)为：

\[(y_1z_2 - z_1y_2)^2+(z_1x_2 - x_1z_2)^2+(x_1y_2 - y_1x_2)^2 \]

展开后，可得：

\[({y_1z_2})^2+({z_1y_2})^2+({z_1x_2})^2+({x_1z_2})^2+({x_1y_2})^2+({y_1x_2})^2 - 2y_1y_2z_1z_2 -2x_1x_2z_1z_2 - 2x_1x_2y_1y_2 \]

等价于：

\[({x_1}^2 + {y_1}^2 + {z_1}^2) \times\ ({x_2}^2 + {y_2}^2 + {z_2}^2) - (x_1x_2 + y_1y_2 + z_1z_2)^2 \]

等价于：

\[||\vec a||^2||\vec b||^2 - (\vec a \cdot \vec b)^2 \]

等价于：

\[||\vec a||^2||\vec b||^2 - (||\vec a||||\vec b||cos\theta)^2 \]

等价于：

\[||\vec m||^2 = ||\vec a||^2||\vec b||^2(1- cos\theta^2) = ||\vec a||^2||\vec b||^2sin\theta^2 \]

所以：

\[||\vec m|| = ||\vec a||||\vec b||sin\theta \]

那么，\(||\vec b||sin\theta\)的另一层含义是什么？

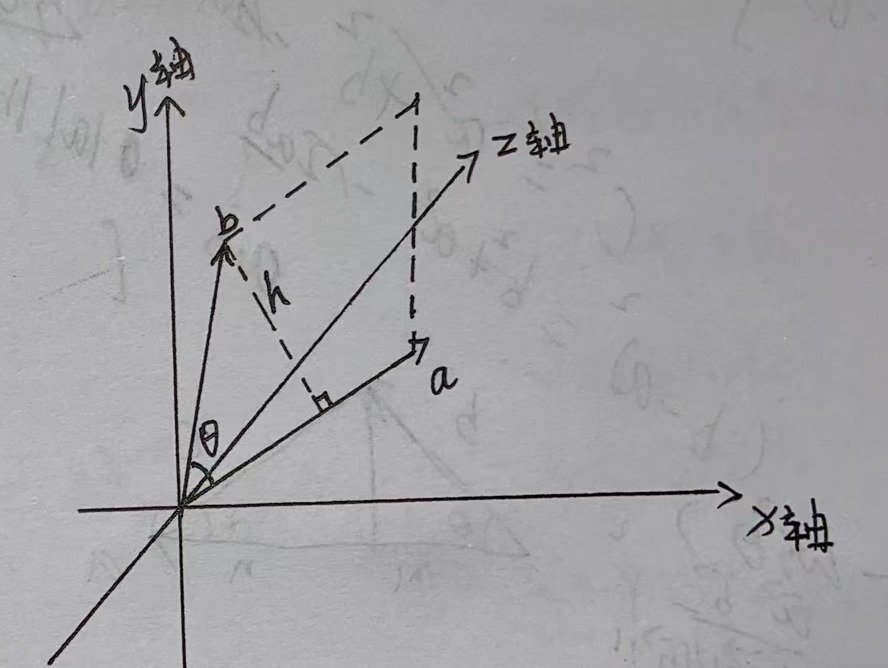
由上图可知，\(||\vec b||sin\theta = h\)，而\(h\)垂直于\(\vec a\)，那么：

\[||\vec m|| = ||\vec a||||\vec b||sin\theta = ||\vec a||h \]

这可以看作是：\(\vec a\)和\(\vec b\)构成的平行四边形的面积（底乘以高）。

也就是说，\(\vec a \times \vec b\)的长度为\(\vec a\)和\(\vec b\)构成的平行四边形的面积。

向量叉积的方向

叉积是个向量呀，现在知道了大小，那方向了？

首先，我们知道：\(\vec m = \vec a \times\ \vec b\)

那么我们先来计算：\(\vec m \cdot \vec a\)

\[\vec m \cdot \vec a = \begin{bmatrix} y_1z_2 - z_1y_2 \\ z_1x_2 - x_1z_2 \\ x_1y_2 - y_1x_2 \\ \end{bmatrix} \cdot \begin{bmatrix} x_1 \\ y_1 \\ z_1 \\ \end{bmatrix} \]

展开：

\[\vec m \cdot \vec a = x_1y_1z_2 - x_1y_2z_1 + x_2y_1z_1 - x_1y_1z_2 + x_1y_2z_1 - x_2y_1z_1 = 0 \]

得到：\(\vec m \cdot \vec a = 0\)，这意味着：\(\vec m\)垂直于\(\vec a\) !!!

以同样的方式计算\(\vec m \cdot \vec b\)，依然会得到相同的结果，也就是说：\(\vec m\)垂直于\(\vec b\) !!!

更进一步说：\(\vec m\)垂直于\(\vec a\)和\(\vec b\)构成的平面。

可是，垂直于平面的向量可能有两个方向啊，如何确定是哪个方向了？

例如：\(\vec a \times\ \vec b\)

1、对于右手坐标系

右手握拳，竖起大拇指。如果从你的视点\(\vec a\)到\(\vec b\)是逆时针旋转，那么大拇指的指向也就是叉积的方向指向你；顺时针，则指向远离你的方向。

2、对于坐手坐标系

左手握拳，竖起大拇指。如果从你的视点\(\vec a\)到\(\vec b\)是顺时针旋转，那么大拇指的指向也就是叉积的方向指向你；逆时针，则指向远离你的方向。

关于向量叉积的一些参考链接：
https://www.shuxuele.com/algebra/vectors-cross-product.html

另，3Blue1Brown关于叉积的笔记