【leetcode】910. Smallest Range II
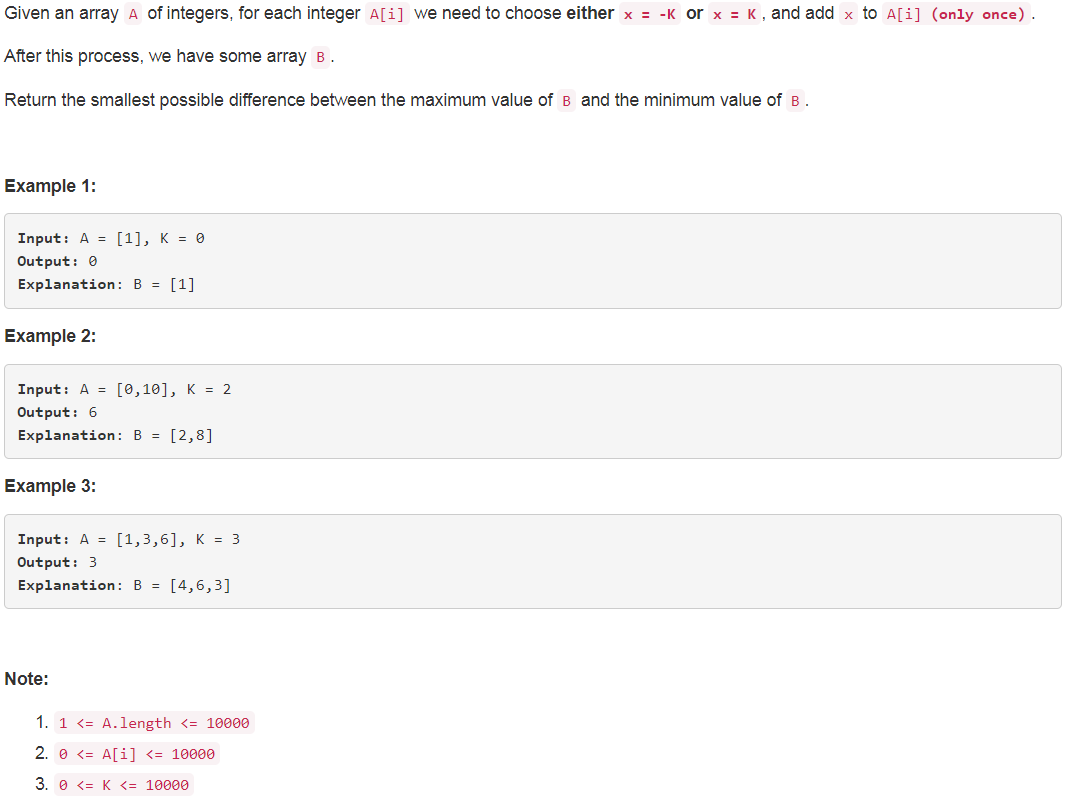
题目如下:
解题思路:我的思路是先找出最大值。对于数组中任意一个元素A[i]来说,如果A[i] + K 是B中的最大值,那么意味着从A[i+1]开始的元素都要减去K,即如果有A[i] + K >= A[-1] - K,那么A[i] + K 就可以作为最大值而存在;如果A[i] + K是最大值,那么最大的最小值是多少呢?因为A[i] 左边的元素都比A[i]小,所以其左边的元素都可以加上K,最大的最小值就会在 A[0] + K 和 A[i+1] - K 之间产生。遍历数组,计算每一个A[i] + K 作为最大值的时候最大值和最小值的差值即可。这里还需要考虑一个特殊情况,就是A[-1] - K 作为最大值。如果是这样情况,再遍历一次数组,如果A[i] + K <= A[-1] -K,那么最小值就可能是A[i] + K;如果A[i] + K > A[-1] -K,那么最小值可能是A[i] - K 。
代码如下:
class Solution(object): def smallestRangeII(self, A, K): """ :type A: List[int] :type K: int :rtype: int """ A.sort() res = 20000 for i in range(len(A)): # suppose A[i] + K is largest if i == len(A) - 1: res = min(res,A[i] - A[0]) elif A[i] + K > A[-1] - K: diff = A[i] + K - min(A[i+1] - K,A[0] + K) res = min(res,diff) #A[-1] - K is largest maxv = A[-1] - K minv = A[0] + K for i in range(len(A)-1): if A[i] + K <= maxv: continue else: minv = min(A[i] - K ,minv) res = min(res,maxv-minv) return res if res != 20000 else 0


 浙公网安备 33010602011771号
浙公网安备 33010602011771号