【leetcode】84. Largest Rectangle in Histogram
题目如下:
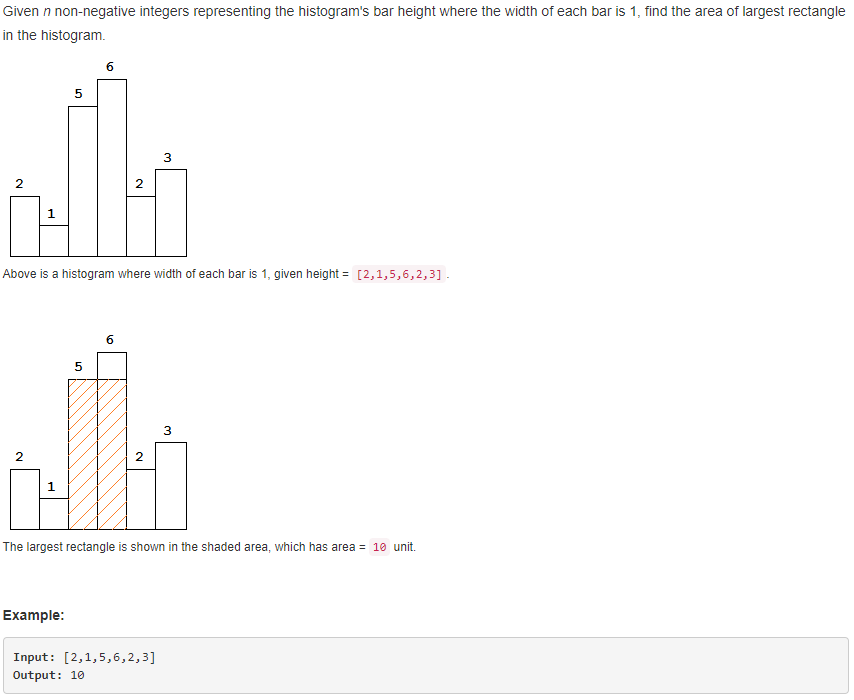
解题思路:这个问题考的是木桶原理,所以我们的关注点就是找到最短的木板。假设Largest Rectangle 的区间是从heights[i-j],并且heights[k]是其中最短的木板,那么可以得出heights[k] > heightsv[i-1] (i > 0) 以及 heights[k] > heightsv[j+1] (j < len(heights)-1)。换句话说,我们只需要遍历一遍heights,计算出以数组中所有元素作为最短木板的Rectangle的面积,取其中最大值即可。对于任意元素heights[k],只需要往左右两边分别找到最近的小于自身的元素,那么这个Rectangle就是heights[k]作为最短木板的最大Rectangle。如何求出左右两边最近的小于自身的元素呢?可以用动态规划。以左边为例,1.如果heights[k] > heights[k-1] ,那么显然dp[k] = k-1;否则,比较heights[k] 与 heights[dp[k-1]],多次循环直到找出比自己小的值即可。
代码如下:
class Solution(object): def largestRectangleArea(self, heights): """ :type heights: List[int] :rtype: int """ if len(heights) ==0 : return 0 dp_left = [0] * len(heights) dp_left[0] = -1 for i in xrange(1,len(dp_left)): j = i - 1 while heights[i] <= heights[j] and j != -1: j = dp_left[j] dp_left[i] = j #print dp dp_right = [0] * len(heights) dp_right[-1] = len(heights) for i in xrange(len(dp_right)-2,-1,-1): j = i + 1 while j != len(heights) and heights[i] <= heights[j]: j = dp_right[j] dp_right[i] = j #print dp2 res = 0 for i,v in enumerate(heights): left = dp_left[i] right = dp_right[i] #print left,right,v res = max(res,(right-left-1)*v) return res


 浙公网安备 33010602011771号
浙公网安备 33010602011771号