【leetcode】778. Swim in Rising Water
题目如下:
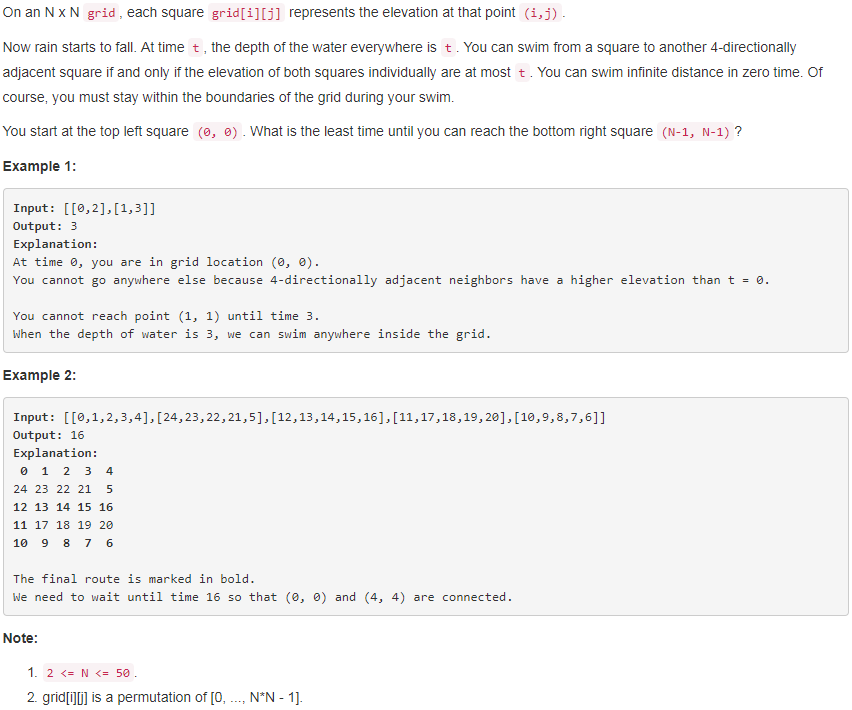
解题思路:本题题干中提到了一个非常重要的前提:"You can swim infinite distance in zero time",同时也给了一个干扰条件,那就是示例2里面的说明,"We need to wait until time 16 so that (0, 0) and (4, 4) are connected."。那么,游泳的人是否需要先游到(1,4)这个点然后等待到time16呢?把问题简化一下,游泳者可以直接在(0,0)等待到time16,这样问题就变成了在什么时间点,游泳的人可以从起点游到终点。在某一特定时间点,矩阵中所有大于这个时间的元素认为是障碍,这样是不是就是一个迷宫问题了?至于怎么找到最小的时间点,首先可以确定,最大的时间是矩阵中值最大的元素,最小的时间是起点元素和终点元素的较大值。显然,用二分查找非常合适。
代码如下:
class Solution(object): def canReach(self,time,matrix): tl = [0] * len(matrix[0]) visit = [] for i in matrix: visit.append(tl[:]) row = len(matrix) column = len(matrix[0]) queue = [(0,0)] visit[0][0] = 1 while len(queue) > 0: x,y = queue.pop(0) #print x,y if x == row-1 and y == column-1: return True if x - 1 >= 0 and matrix[x-1][y] <= time and visit[x-1][y] == 0: queue.append((x-1,y)) visit[x-1][y] = 1 if x + 1 < row and matrix[x+1][y] <= time and visit[x+1][y] == 0: queue.append((x+1,y)) visit[x+1][y] = 1 if y - 1 >= 0 and matrix[x][y-1] <= time and visit[x][y-1] == 0: queue.append((x,y-1)) visit[x][y-1] = 1 if y + 1 < column and matrix[x][y+1] <= time and visit[x][y+1] == 0: queue.append((x,y+1)) visit[x][y+1] = 1 return False def swimInWater(self, grid): """ :type grid: List[List[int]] :rtype: int """ low = max(grid[0][0],grid[-1][-1]) high = low for i in grid: for j in i: high = max(j,high) res = len(grid)*len(grid) while low <= high: mid = (low + high) / 2 if self.canReach(mid,grid) == True: res = min(res,mid) high = mid - 1 else: low = mid + 1 return res


 浙公网安备 33010602011771号
浙公网安备 33010602011771号