【leetcode】861. Score After Flipping Matrix
题目如下:
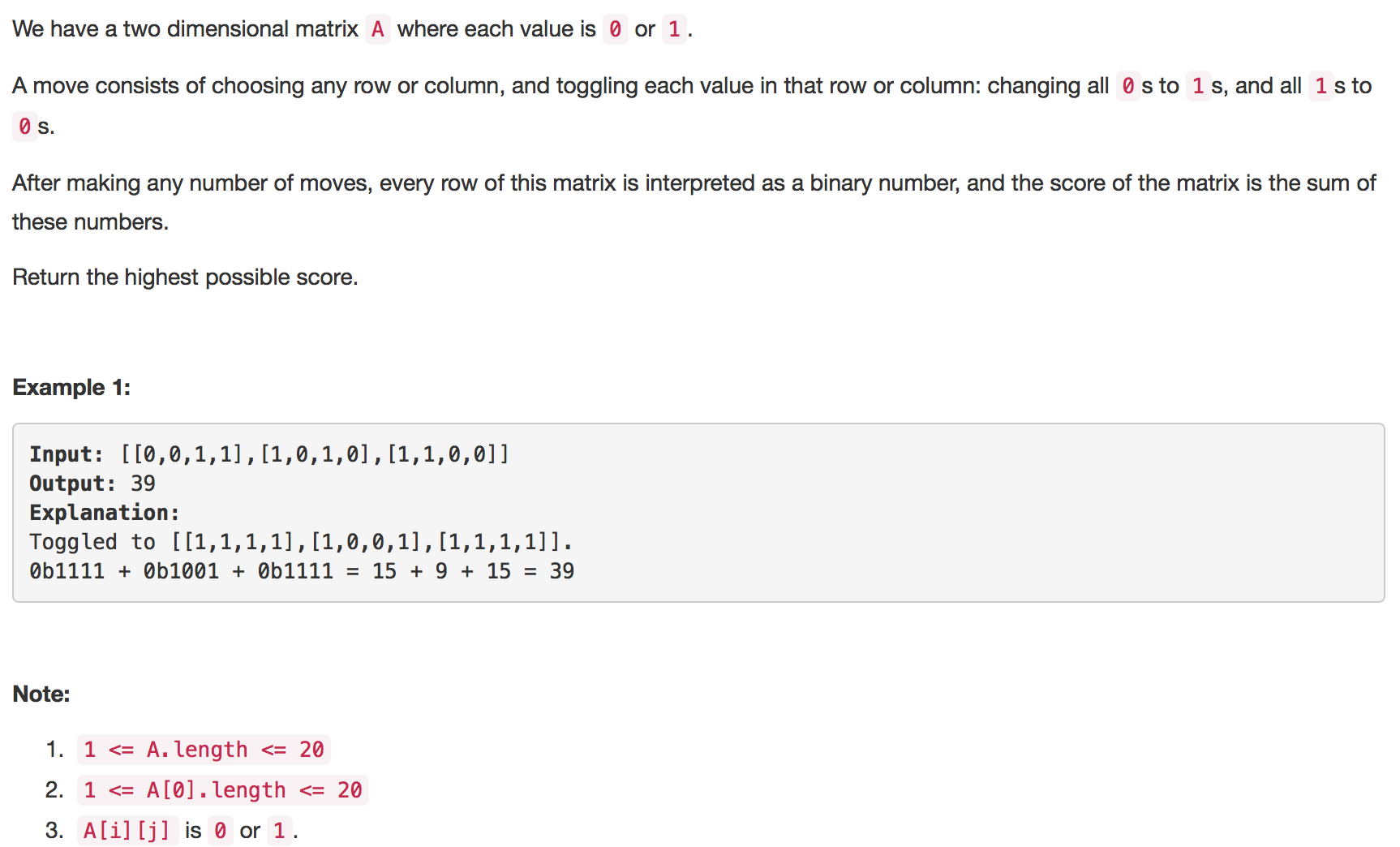
解题思路:本题需要知道一个数字规律,即pow(2,n) > sum(pow(2,0)+pow(2,1)+...+pow(2,n-1))。所以,为了获得最大值,要保证所有行的最高位是1,即需要优先进行行变换,把最高位变成1。接下来就是列变换,把0多于1的列做变换变成1多于0的列即可。
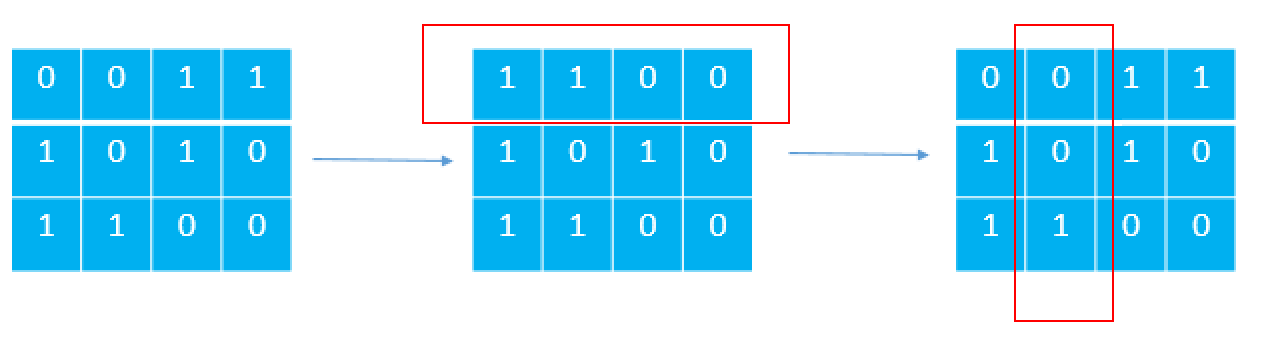 代码如下:
代码如下:
class Solution(object): def matrixScore(self, A): """ :type A: List[List[int]] :rtype: int """ if len(A) == 0 or len(A[0]) == 0: return 0 #set the highest bit to 1.Since pow(2,N) > sum(pow(2,0) + pow(2,1) + ...+pow(2,n-1) for i in range(len(A)): if A[i][0] == 1: continue else: for j in range(len(A[i])): if A[i][j] == 0: A[i][j] = 1 else: A[i][j] = 0 row = len(A) column = len(A[0]) for i in range(column): count1 = 0 count0 = 0 for j in range(row): if A[j][i] == 0: count0 += 1 else: count1 += 1 if count0 > count1: #convert for j in range(row): if A[j][i] == 0: A[j][i] = 1 else: A[j][i] = 0 res = 0 for i in A: v = ''.join([str(j) for j in i]) res += int(v,2) return res


 浙公网安备 33010602011771号
浙公网安备 33010602011771号