【leetcode】698. Partition to K Equal Sum Subsets
题目如下:
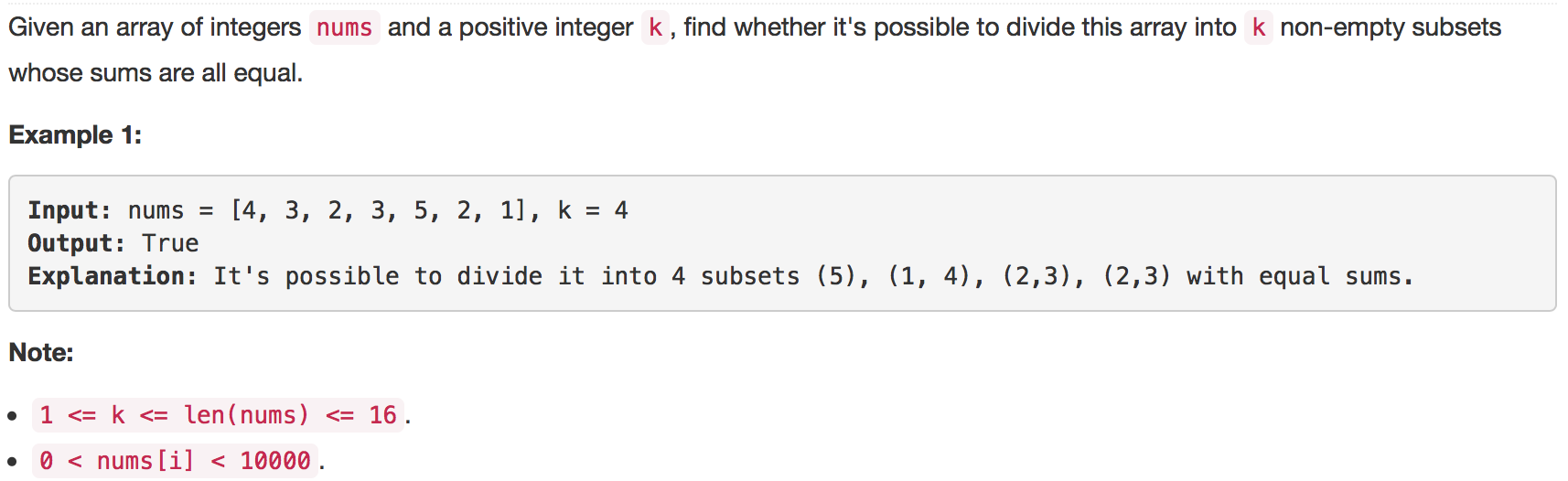
解题思路:本题是【leetcode】473. Matchsticks to Square的姊妹篇,唯一的区别是【leetcode】473. Matchsticks to Square指定了分成四个子数组,而本题分成的份数不定,作为参数输入。另外,本题的测试用例好像复杂一点,因此我过滤掉了nums中值等于avg的元素,不参与后面的DFS计算,提高效率。
代码如下:
class Solution(object): def canPartitionKSubsets(self, nums, k): """ :type nums: List[int] :type k: int :rtype: bool """ border = k if sum(nums) % border != 0: return False avg = sum(nums) / border #过滤掉了nums中值等于avg的元素,不参与后面的DFS计算 newnums = [] for i in nums: if i == avg: border -= 1 continue newnums.append(i) nums = newnums[:] nums.sort() queue = [[x] for x in xrange(len(nums))] res = [] visit = [0 for x in xrange(len(nums))] while len(queue) > 0: nl = queue.pop(0) amount = 0 for i in nl: amount += nums[i] if amount == avg: res.append(nl) for i in nl: visit[i] = 1 continue tl = [] for i in xrange(nl[-1] + 1, len(nums)): if amount + nums[i] <= avg: tl = nl[:] tl.append(i) queue.append(tl) if len(res) < border: return False if sum(visit) != len(visit): return False queue = [] for i in res: queue.append((set(i), 1)) # print queue while len(queue) > 0: ns, count = queue.pop(0) if count == border and len(ns) == len(nums): # print ns return True for i in res: # print ns | set(i) if len(ns | set(i)) == len(ns) + len(i): queue.insert(0, (ns | set(i), count + 1)) return False


 浙公网安备 33010602011771号
浙公网安备 33010602011771号