【leetcode】Champagne Tower

题目如下：

 

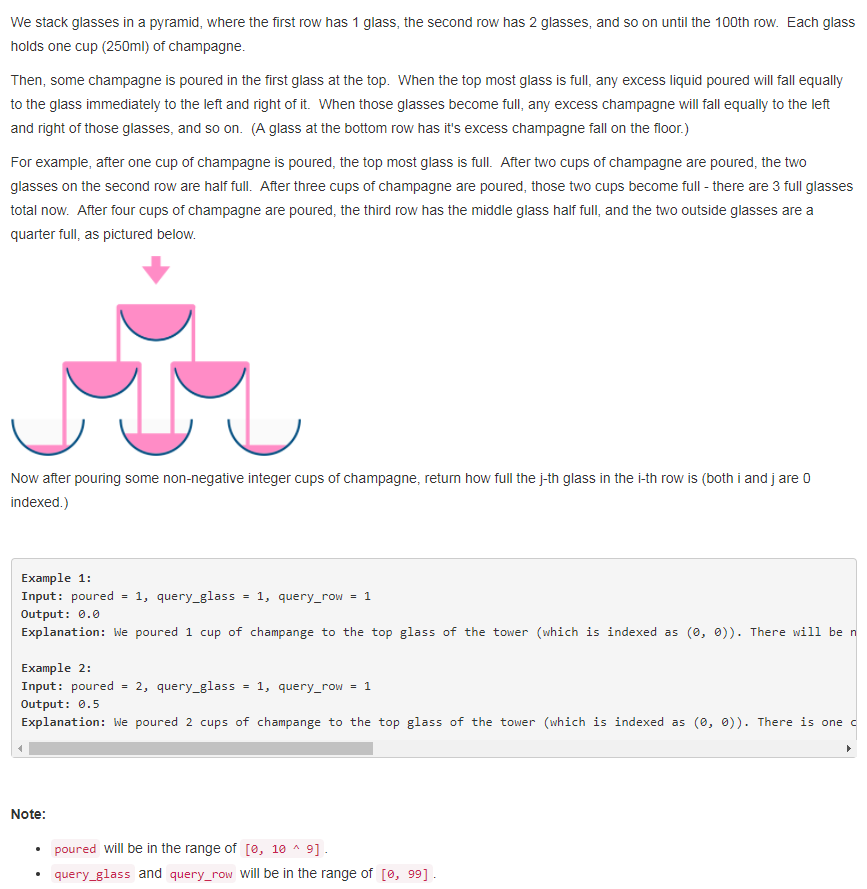
解题思路：本题如果用递归来做，思路会非常清晰。每个杯子得到的总的香槟的数量，减去自身杯子容量后，多余的部分均分成两部分，下层的两个杯子各得一半，但是这种解法在输入香槟较大的情况下会导致超时。更加合适的是用动态规划的方法，因为递推关系式很容易就能找到。对于任意一个杯子dp[i][j]来说，它的输入来自于dp[i-1][j]和dp[i-1][j-1]溢出的部分的一半，所以表达式为 dp[i][j] =  max(0,(dp[i-1][j] - 1)/2) + max(0,(dp[i-1][j-1]-1)/2)。

代码如下：

class Solution(object):
    def champagneTower(self, poured, query_row, query_glass):
        """
        :type poured: int
        :type query_row: int
        :type query_glass: int
        :rtype: float
        """
        dp = []
        level = 100
        for x in range(level):
            l = [0.0 for x in range(level)]
            dp.append(l)
        dp[0][0] = poured
        for i in range(1,query_row+1):
            for j in range(query_glass+1):
                dp[i][j] += max(0,float(dp[i-1][j] - 1)/2)
                if j-1 >= 0:
                    dp[i][j] += max(0,float(dp[i-1][j-1]-1)/2)
        return min(1,dp[query_row][query_glass])