【leetcode】1319. Number of Operations to Make Network Connected
题目如下:
There are
ncomputers numbered from0ton-1connected by ethernet cablesconnectionsforming a network whereconnections[i] = [a, b]represents a connection between computersaandb. Any computer can reach any other computer directly or indirectly through the network.Given an initial computer network
connections. You can extract certain cables between two directly connected computers, and place them between any pair of disconnected computers to make them directly connected. Return the minimum number of times you need to do this in order to make all the computers connected. If it's not possible, return -1.Example 1:
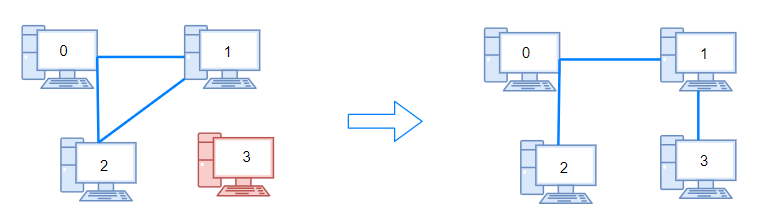
Input: n = 4, connections = [[0,1],[0,2],[1,2]] Output: 1 Explanation: Remove cable between computer 1 and 2 and place between computers 1 and 3.Example 2:
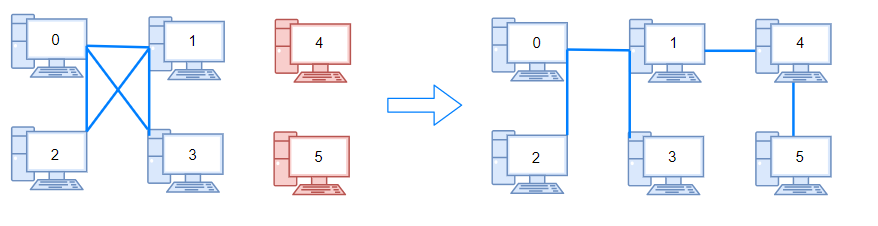
Input: n = 6, connections = [[0,1],[0,2],[0,3],[1,2],[1,3]] Output: 2Example 3:
Input: n = 6, connections = [[0,1],[0,2],[0,3],[1,2]] Output: -1 Explanation: There are not enough cables.Example 4:
Input: n = 5, connections = [[0,1],[0,2],[3,4],[2,3]] Output: 0Constraints:
1 <= n <= 10^51 <= connections.length <= min(n*(n-1)/2, 10^5)connections[i].length == 20 <= connections[i][0], connections[i][1] < nconnections[i][0] != connections[i][1]- There are no repeated connections.
- No two computers are connected by more than one cable.
解题思路:并查集。先把 connections 中所有配对的元素组成并查集,如果两个元素已经有共同的祖先,说明这个 connection 是多余的,可以打断用来和其他元素连接。最后,只需要比较 多余的 connections 数量 与 并查集 组的个数即可。
代码如下:
class Solution(object): def makeConnected(self, n, connections): """ :type n: int :type connections: List[List[int]] :rtype: int """ self.redundant = 0 parent = [i for i in range(n)] def find(v1): if parent[v1] == v1: return v1 return find(parent[v1]) def union(v1,v2): p1 = find(v1) p2 = find(v2) if p1 == p2: self.redundant += 1 elif p1 > p2: parent[p1] = p2 else: parent[p2] = p1 for (x,y) in connections: union(x,y) dic_parent = {} for i in range(n): p = find(i) dic_parent[p] = 1 if len(dic_parent) - 1 > self.redundant: return -1 return len(dic_parent) - 1

 浙公网安备 33010602011771号
浙公网安备 33010602011771号