【leetcode】963. Minimum Area Rectangle II

题目如下：

Given a set of points in the xy-plane, determine the minimum area of any rectangle formed from these points, with sides not necessarily parallel to the x and y axes.

If there isn't any rectangle, return 0.

 

Example 1:

Input: [[1,2],[2,1],[1,0],[0,1]]
Output: 2.00000
Explanation: The minimum area rectangle occurs at [1,2],[2,1],[1,0],[0,1], with an area of 2.

Example 2:

Input: [[0,1],[2,1],[1,1],[1,0],[2,0]]
Output: 1.00000
Explanation: The minimum area rectangle occurs at [1,0],[1,1],[2,1],[2,0], with an area of 1.

Example 3:

Input: [[0,3],[1,2],[3,1],[1,3],[2,1]]
Output: 0
Explanation: There is no possible rectangle to form from these points.

Example 4:

Input: [[3,1],[1,1],[0,1],[2,1],[3,3],[3,2],[0,2],[2,3]]
Output: 2.00000
Explanation: The minimum area rectangle occurs at [2,1],[2,3],[3,3],[3,1], with an area of 2.

 

Note:

1. 1 <= points.length <= 50
2. 0 <= points[i][0] <= 40000
3. 0 <= points[i][1] <= 40000
4. All points are distinct.
5. Answers within 10^-5 of the actual value will be accepted as correct.

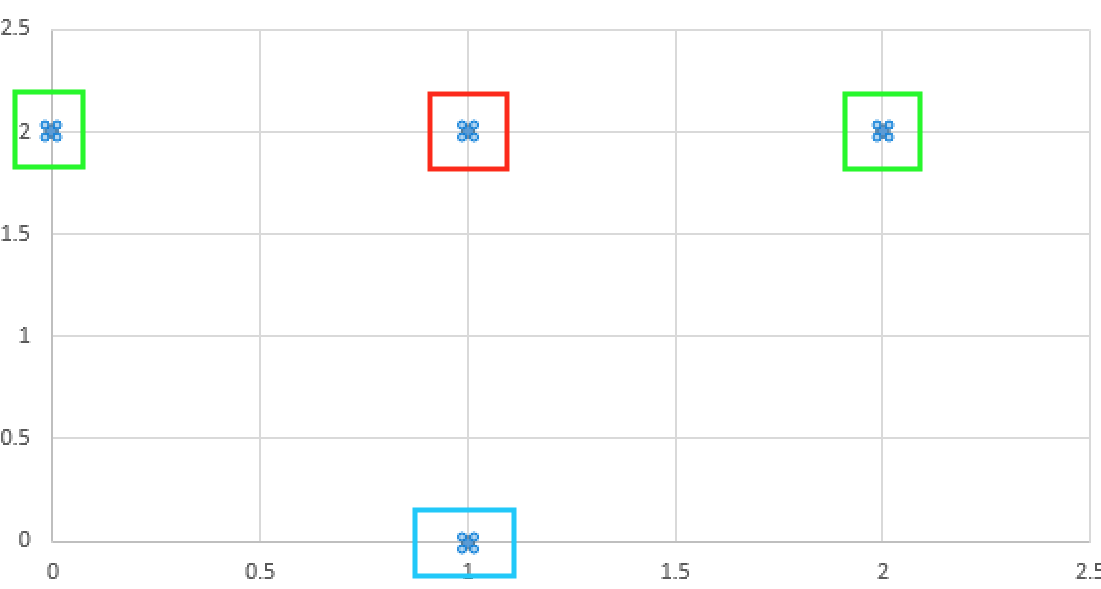
解题思路：本题是【leetcode】939. Minimum Area Rectangle 的升级版，由于题目要求矩形不需要和X轴或者Y轴平行，因此我的解法就是简单粗暴。从points中任意取出四个点判断是否是矩形，这样的话时间复杂度是O(n^4)，虽然points.length最大只有50，但还是华丽丽的超时。 那就优化吧，我们可以以边为单位，假设两条边要组成矩形平行的边，那么这两条边的长度一定是相同的，所以可以实现把任意两个点组成的边的长度都计算出来，接下来再从长度相同的两条边中判断是否组成矩形，时间复杂度就降为O(n^2)了，和【leetcode】4Sum 的思路非常相似。如果两条边的长度相同，怎么判断是否能组成矩形呢，那就用勾股定理了，取这两条边的任意一点，分别计算出与其他三点的距离，判断是否满足勾股定理。看起来似乎是这样，但是有如下这种情况，红框点到两个绿框点的距离与红框点到蓝框点的距离是满足勾股定理的，但实际上这四个点并没有组成矩形。所以找出了四个点后，不能只判断其中一个点与其他三个点的距离，至少应该取其中两个来做判断（感觉是这样，但我不确定，所以我取了三个点判断），最后求出最小的面积即可。

代码如下：

class Solution(object):
    def minAreaFreeRect(self, points):
        """
        :type points: List[List[int]]
        :rtype: float
        """
        def dis(p1, p2):
            return (p1[0] - p2[0]) ** 2 + (p1[1] - p2[1]) ** 2
        dic = {}
        res = float('inf')
        for i in range(len(points)):
            for j in range(i+1,len(points)):
                d =  dis(points[i], points[j])
                if d not in dic:
                    dic[d] = [(i,j)]
                else:
                    dic[d].append((i,j))
        for pl in dic.itervalues():
            for i in range(len(pl)):
                for j in range(i + 1, len(pl)):
                    if len(set(pl[i]) & set(pl[j])) > 0:
                        continue
                    p1,p2,p3,p4 = pl[i][0],pl[i][1],pl[j][0],pl[j][1]
                    d1 = dis(points[p1], points[p2])
                    d2 = dis(points[p1], points[p3])
                    d3 = dis(points[p1], points[p4])
                    dl = sorted([d1, d2, d3])
                    if dl[0] + dl[1] != dl[2]:
                        continue

                    d1 = dis(points[p2], points[p1])
                    d2 = dis(points[p2], points[p3])
                    d3 = dis(points[p2], points[p4])
                    dl = sorted([d1, d2, d3])
                    if dl[0] + dl[1] != dl[2]:
                        continue

                    d1 = dis(points[p3], points[p1])
                    d2 = dis(points[p3], points[p2])
                    d3 = dis(points[p3], points[p4])
                    dl = sorted([d1, d2, d3])
                    if dl[0] + dl[1] != dl[2]:
                        continue

                    res = min(res, dl[0] * dl[1])

        if res == float('inf'):
            res = 0
        import math
        return math.sqrt(res)