webgl学习(一)——camer的lookAt
webgl学习(一)——camer的lookAt
首先我们需要知道相机的期望位置,将它叫做cameraPosition, 然后需要知道看向或对准的目标位置,将它叫做target。 如果将target减去cameraPosition就会得到相机的朝向, 将它叫做zAxis。由于我们知道相机看向的是 -Z 方向, 所以可以用另一种方式相减cameraPosition - target, 将结果单位化后直接赋给矩阵的z区域。

矩阵的这个区域代表的是 Z 轴。在这个例子中相机的 Z-axis 进行了单位化, 单位化也就是一个做一个类似 1.0 的矢量;

这些信息还不够,只给了一个单位圆上点,如何来确定物体的姿态呢? 这就需要填充矩阵的其他区域,尤其是 X 轴和 Y 轴。通常情况下我们知道它们互相垂直, 如果再知道哪里是上方,在该例中是(0,1,0),就可以使用“叉乘”去计算矩阵的 X 轴和 Y 轴。
我不知道叉乘的数学意义是什么,但我知道将两个单位向量叉乘后可以得到一个和它们都垂直的向量。 换句话说,如果你有一个向量指向东南方,一个向量指向上方, 叉乘后会得到一个指向西南方或东北方的矢量,因为这两个矢量都和东南方和上方垂直。 相乘的顺序不同的到结果相反。
在任何情况下我们可以通过叉乘zAxis 和up 得到相机的xAxis。
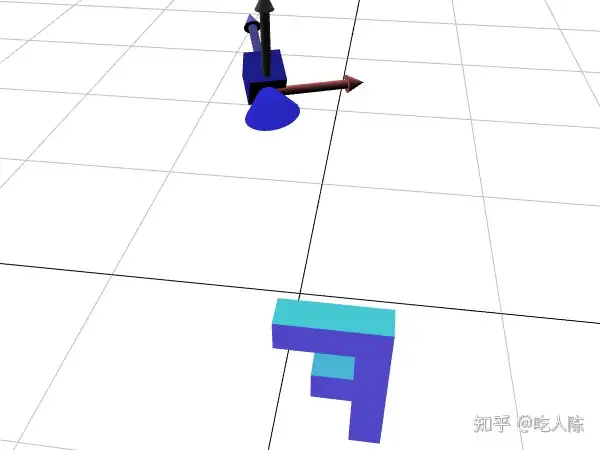
现在我们有了 xAxis , 可以叉乘 zAxis 和 xAxis 的到相机的 yAxis。

现在将三个轴插入矩阵中,会给我们提供一个从 cameraPosition 指向 target 的转换,只需要再加上 position

这是计算叉乘的代码
function cross(a, b) {
return [a[1] * b[2] - a[2] * b[1],
a[2] * b[0] - a[0] * b[2],
a[0] * b[1] - a[1] * b[0]];
}
这是向量相减的代码
function subtractVectors(a, b) {
return [a[0] - b[0], a[1] - b[1], a[2] - b[2]];
}这是单位化向量的代码
function normalize(v) {
var length = Math.sqrt(v[0] * v[0] + v[1] * v[1] + v[2] * v[2]);
// 确定不会除以 0
if (length > 0.00001) {
return [v[0] / length, v[1] / length, v[2] / length];
} else {
return [0, 0, 0];
}
}这是计算“朝向”矩阵的代码
var m4 = {
lookAt: function(cameraPosition, target, up) {
var zAxis = normalize(
subtractVectors(cameraPosition, target));
var xAxis = normalize(cross(up, zAxis));
var yAxis = normalize(cross(zAxis, xAxis));
return [
xAxis[0], xAxis[1], xAxis[2], 0,
yAxis[0], yAxis[1], yAxis[2], 0,
zAxis[0], zAxis[1], zAxis[2], 0,
cameraPosition[0],
cameraPosition[1],
cameraPosition[2],
1,
];
}
有啥用:
根据fov、aspect、near、far构建了一个默认为相机位置在原点, 且看向z轴负方向的视锥;
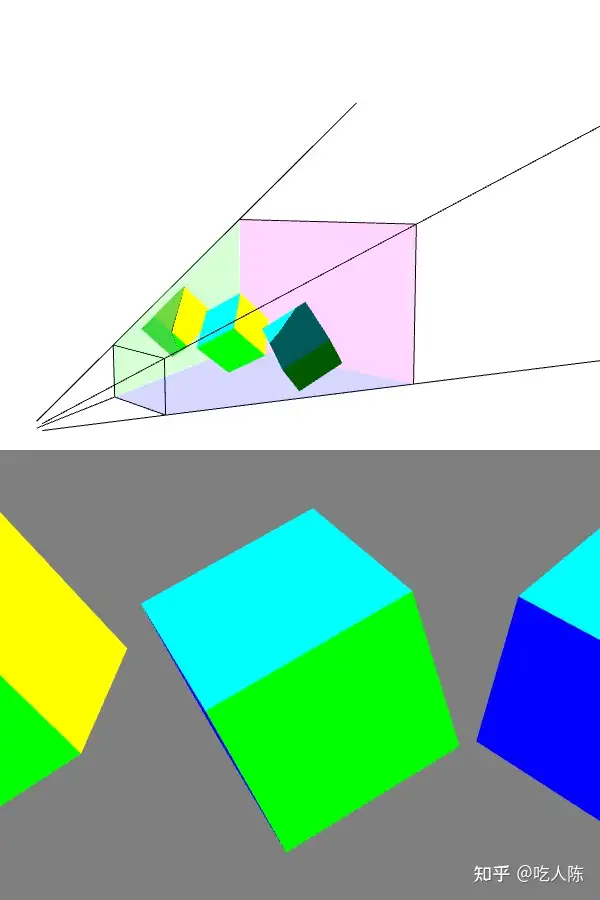
但相机位置肯定是随意变换的,lookAt就是变化依据:
// 默认位置的相机视锥
var projectionMatrix = m4.perspective(fieldOfViewRadians, aspect, zNear, zFar);
// 任意位置的矩阵
var cameraMatrix = m4.lookAt(cameraPosition, fPosition, up);
// 得到最终的视锥构建
var viewProjectionMatrix = m4.multiply(projectionMatrix, viewMatrix);应用到着色器中:
gl_Position = viewProjectionMatrix * a_position; // 即可计算出顶点在当前视视锥下的坐标位置点



