luoguP3372 【模板】线段树 1
emmm
今天gg没讲课,青青姐给我讲了线段树
(讲得太好了!我们来膜一下!%%%
(然后我就是来讲讲我听完后的感受的,大家重点在于夸青青姐tql
像我这样的蒟蒻,看到线段树的第一反应是。。。
“???
???
行吧,姐给我讲讲呗。”

(姐太强了!
(姐太巨了!
(不愧是我姐!
然后我们就来看看线段树是神马东西吧~
(上网找的线段树图片。感谢图源【虽然不知道需不需要声明,但是侵删
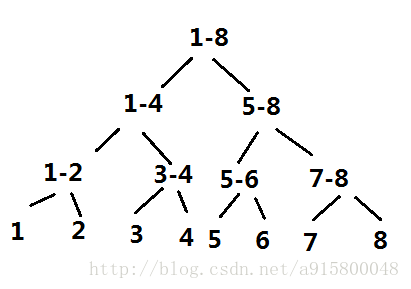
先来了解一下线段树
每个父节点包含着子节点的信息
而每个叶子节点包含着一个元素
我们如果要对1-5进行操作,我们可以利用线段树进行简化,只操作1-4这个父节点和5这个叶子节点
这里引用luogu题解一句话:通过将整个序列分为有穷个小块,对于要查询的一段区间,总是可以整合成k个所分块与m个单个元素的信息的并集(0<=k,m<=n)
如果我们按照从左到右,自上而下的顺序给树的每一个节点编号,第一层为1,第二层是2和3,第三层是4,5,6,7,以此类推,我们会发现,每个下标为i的父节点的左子节点下标为i * 2,右子节点下标为i * 2 + 1
了解了线段树的基本思路,我们就可以尝试建一棵树了
1 void build(int L,int R,int now){ 2 lazy[now] = 0;//这个是待会在修改区间时用于简化的懒标记 3 l[now] = L; 4 r[now] = R; 5 if(L == R){//显然,L,R相等时位于叶子节点,可以进行赋值操作 6 scanf("%lld",&sum[now]);//当前这一层的总和(只有一个数(因为这道题求总和,不然还可以进行取最大或最小的操作 7 return ; 8 } 9 int mid = (L + R)>>1;//二分优化 10 build(L,mid,now * 2);//左右的子树都要赋值 11 build(mid + 1,R,now * 2 + 1); 12 sum[now] = sum[now * 2] + sum[now * 2 + 1];//当前这一层为左右子节点信息的总和 13 }
建完树之后要进行修改操作
1 void modify(int L,int R,int k,int now){//L,R为进行修改的区间,k为修改的值,now为当前层数(每一次的修改,建树,搜索都是从第一层开始的,所以now总是赋为1 2 if(l[now] == L && r[now] == R) { 3 lazy[now] += k;//懒标记,记录该层以下需要进行的修改操作,减少操作次数,当需要使用下层的元素时再进行修改 4 return ; 5 } 6 sum[now] += (long long)(R -L + 1) * k;//该层总共修改的值为以下子节点修改值的总和 7 int mid = (l[now] + r[now])>>1; 8 if(R <= mid) return modify(L,R,k,now * 2);//完全在左子树是时 9 else if(L >= mid + 1) modify(L,R,k,now * 2 + 1);//在右子树 10 else {//两边都需要修改 11 modify(L,mid,k,now * 2); 12 modify(mid + 1,R,k,now * 2 + 1); 13 } 14 }
已经使用了懒标记,我们可以查询每段区间修改后的值,并看看懒标记的下移
long long query(int L,int R,int now){ sum[now] += lazy[now] * (r[now] - l[now] + 1);//当层修改 lazy[now * 2] += lazy[now];//懒标记下移 lazy[now * 2 + 1] += lazy[now]; lazy[now] = 0;//下移后清零 if(l[now] == L && r[now] == R)return sum[now]; int mid = (l[now] + r[now])>>1; if(R <= mid) return query(L,R,now * 2); else if(L >= mid + 1) return query(L,R,now * 2 + 1); else return query(L,mid,now * 2) + query(mid + 1,R,now * 2 + 1); }
这样线段树的主体部分就写完了
这道题是一道板子题,所以只需要把以上的代码写出来,再写主函数就大功告成了
#include<cstdio> using namespace std; const int maxn = 100005; int n,m,a,b,c; long long sum[4 * maxn],lazy[8 * maxn],k;//注意要开大一些 int l[4 * maxn],r[4 * maxn]; void build(int L,int R,int now){ lazy[now] = 0; l[now] = L; r[now] = R; if(L == R){ scanf("%lld",&sum[now]); return ; } int mid = (L + R)>>1; build(L,mid,now * 2); build(mid + 1,R,now * 2 + 1); sum[now] = sum[now * 2] + sum[now * 2 + 1]; } long long query(int L,int R,int now){ sum[now] += lazy[now] * (r[now] - l[now] + 1); lazy[now * 2] += lazy[now]; lazy[now * 2 + 1] += lazy[now]; lazy[now] = 0; if(l[now] == L && r[now] == R)return sum[now]; int mid = (l[now] + r[now])>>1; if(R <= mid) return query(L,R,now * 2); else if(L >= mid + 1) return query(L,R,now * 2 + 1); else return query(L,mid,now * 2) + query(mid + 1,R,now * 2 + 1); } void modify(int L,int R,int k,int now){ if(l[now] == L && r[now] == R) { lazy[now] += k; return ; } sum[now] += (long long)(R -L + 1) * k; int mid = (l[now] + r[now])>>1; if(R <= mid) return modify(L,R,k,now * 2); else if(L >= mid + 1) modify(L,R,k,now * 2 + 1); else { modify(L,mid,k,now * 2); modify(mid + 1,R,k,now * 2 + 1); } } int main(){ scanf("%d%d",&n,&m); build(1,n,1); for(int i = 0;i < m;i++){ scanf("%d",&a); if(a == 1){ scanf("%d%d%lld",&b,&c,&k); modify(b,c,k,1); } if(a == 2){ scanf("%d%d",&b,&c); printf("%lld\n",query(b,c,1)); } } return 0; }
这里还要补一句:虽然线段树好像很快,但是它只能维护带有结合律的信息,比如区间max/minmax/min、sumsum、xorxor之类的,但是不带有结合律的信息就不能维护
emmmm
这道题就到这里了
最后让我们再次感谢一下青青姐的讲解!
(写这篇题解大概也是怕自己以后忘


