luogu P2458 [SDOI2006]保安站岗

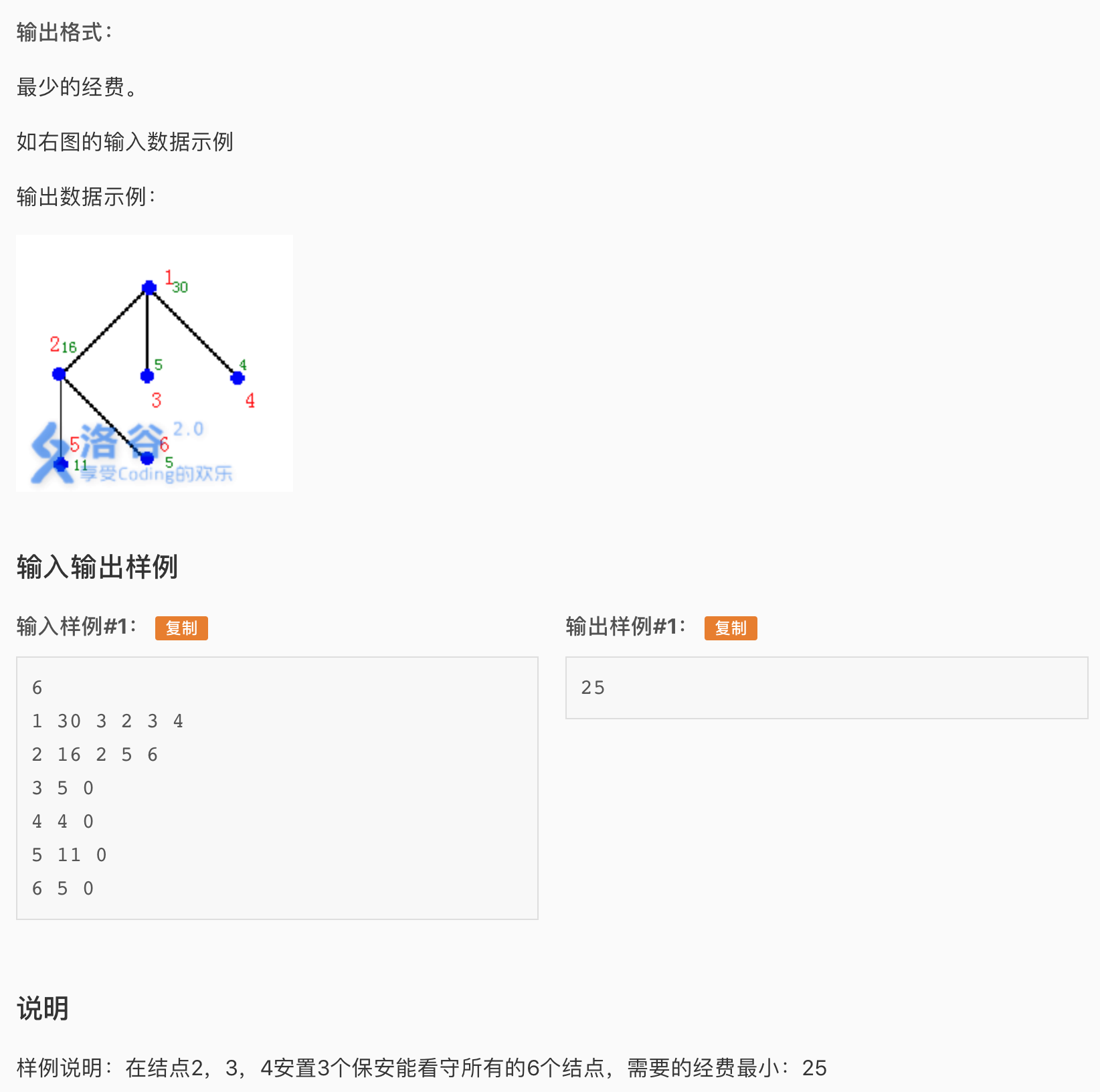
显而易见

树形dp

然而我做了很很很很很久

最后看讨论版才de出来bug

要考虑三个状态

1.父节点有保安

2.本身有保安

3.儿子节点放保安

1.2.douhenhaokaolv

3.不太容易，看了题解才有思路

dp[u][2]：点u没有放置警察，且目前未被任何节点控制。

所以u一定会被它的至少一个儿子控制，换句话来说，u的儿子中，至少有一个要放置警察。不妨设这个儿子为x，那么dp[u][2]的初始值应当为dp[x][0]，对于其它儿子依旧是除了无法选择被父亲控制这种状态其它都可以选。综上dp[u][2]=dp[x][0]+∑v∈son(u)≠xmin(dp[v][0],dp[v][2])

那么现在的问题就是如何得到这个最优的x了，可以这么思考，如果x不是最优的，那么对于x来说，一定存在另一个子节点y满足 dp[y][0]+∑v∈son(u)≠ymin(dp[v][0],dp[v][2])<dp[x][0]+∑v∈son(u)≠xmin(dp[v][0],dp[v][2])

推得dp[x][0]+∑v∈son(u)≠xmin(dp[v][0],dp[v][2])−dp[y][0]−∑v∈son(u)≠ymin(dp[v][0],dp[v][2])>0

两式同时减去相同的部分，有dp[x][0]+min(dp[y][0],dp[y][2])−dp[y][0]−min(dp[x][0],dp[x][2])>0

即dp[x][0]−min(dp[x][0],dp[x][2])>dp[y][0]−min(dp[y][0],dp[y][2])

所以对于最优的节点x，dp[x][0]−min(dp[x][0],dp[x][2])一定是所有子节点中最小的

写完之后一直90分

会WA掉第三个点

讨论版中友情提示

这题的数据有毒,说一下几个坑.

1. 可能不连通,但是不要管,直接以1为根,只算以1为根的联通块的答案就好. 
2. 数据范围和描述不一致,都当成正常的N=1e5,M=2e5的"无向图就好了". 
3. 数据格式有问题,给出的不一定是父亲连向儿子的边,直接建成无向的,dfs的时候判一下v!= fa就好了

 然后存了双向边就过了。。。emmm

#include<cstdio>
#include<algorithm>
using namespace std;
#define maxn 1510

int head[maxn],cnt;
int du[maxn];
int v[maxn];
int dp[maxn][3];

struct EDGE {
    int nxt,to;
} edge[maxn * 2];

void add(int x,int y) {
    edge[++cnt].to = y;
    edge[cnt].nxt = head[x];
    head[x] = cnt;
}

void treedp(int u,int fa) {
    int x = 0;
    dp[u][0] = v[u];
    for(int i = head[u]; i; i = edge[i].nxt) {
        int v = edge[i].to;
        if(v == fa)
        continue;
        treedp(v,u);
        dp[u][0] += min(dp[v][0],min(dp[v][1],dp[v][2]));
//本身放了保安
        dp[u][1] += min(dp[v][0],dp[v][2]);
//父节点放了保安
        if((dp[x][0] - min(dp[x][0],dp[x][2])) > dp[v][0] - min(dp[v][0],dp[v][2]))
            x = v;
//子节点放保安
//        dp[u][1] += min(dp[v][0],dp[v][1]);
//        minn = min(minn,dp[v][1]);
//        printf("dp[%d][1] = %d    dp[%d][0] = %d\n",u,dp[u][1],u,dp[u][0]);
    }
    dp[u][2] = dp[x][0];
    for(int i = head[u]; i; i = edge[i].nxt) {
        int v = edge[i].to;
        if(v == x)
        continue;
        dp[u][2] += min(dp[v][0],dp[v][2]);
    }
}

int main() {
    int n;
    scanf("%d",&n);
    dp[0][0] = 1 << 30;//初始化避免被选
    while(n--) {
        int i,k,m;
        scanf("%d%d%d",&i,&k,&m);
        v[i] = k;
        while(m--) {
            int r;
            scanf("%d",&r);
            add(i,r);
            add(r,i);//村双向
            du[r]++;
            //    printf("orz %d\n",du[i]);
        }
    }
//    for(int i = 1; i <= n; i++)
//        printf("orz %d\n",du[i]);
    int root = 1;
    for(int i =1; i <= n; i++)
        if(du[i] == 0) {
            root = i;
            break;
        }//似乎把1当成根就可以了
//    printf("qwq %d\n",root);
    treedp(root,0);
    printf("%d",min(dp[root][0],dp[root][2]));//根节点没有父节点
    return 0;
}