Java-数据结构
1.基本的三种数据结构类型
- 线性表
- 结点按逻辑关系依次排列形成一个“锁链”
- 树
- 具有分支、层次特性,其形态有点象自然界中的树
- 图
- 结点按逻辑关系互相缠绕,任何两个结点都可以邻接
2.数组就是一种典型的线性表
1、数组其实就是一种典型的线性表，而且是一种物理连续的线性表
2、数组的特点：
-
通过下标（内存偏移量，单位是元素个数）进行元素访问
-
数组中每个元素的类型必须一致
-
数组的大小一旦确定就不能变更
3.链表
1、链表是一种逻辑上连续的线性表，所谓逻辑上连续，指的是节点与节点直接无需在内存上物理连续存储，而是通过引用成员来指向下一个节点的位置。
2、链表解决了数组的如下问题：
-
插入,删除的效率非常低
-
数组大小不可变,无法实现动态生成
3、链表和数组的区别：
-
解决了数组无法动态增长及减小的问题
-
插入删除的效率非常高（已经找到了删除或者插入的位置节点）
-
数组的元素寻址访问效率要高于链表
4、链结点元素定义类叫做Node，每个Node对象中都包含一个对下一个链结点引用的字段(通常叫做next)
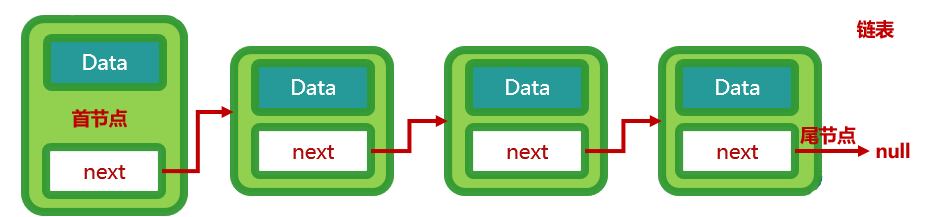
5、定义一个链表和Node节点
- 自定义链表
/** * 自定义链表 * * @param <T> */ public class MyLink<T> { //存储的数据数量 private int size; //链表的头结点，为了算法方便 private Node<T> head = new Node<>(null); /** * 定义链表中节点类（内部类） * * @param <T> */ private class Node<T> { /** * 存储的数据 */ T element; /** * 存储下一个节点 */ Node<T> next; public Node(T element) { this.element = element; } } /** * 指定位置添加数据 * * @param element 数据 * @param index 索引位置 */ public void add(T element, int index) { rangeIndexCheckForAdd(index); //创建新节点 Node<T> newNode = new Node<>(element); Node<T> preNode; if (index == 0) { //index==0的前一个节点是首节点 preNode = this.head; } else { //查找index-1位置的节点对象 preNode = node(index - 1); } //index位置节点 Node<T> indexNode = preNode.next; preNode.next = newNode; newNode.next = indexNode; //size加1 size++; } /** * 根据索引删除元素 * * @param index * @return */ public T remove(int index) { rangeIndexCheck(index); Node<T> preNode; if (index == 0) { //index==0的前一个节点是首节点 preNode = this.head; } else { //查找index-1位置的节点对象 preNode = node(index - 1); } //index位置节点 Node<T> indexNode = preNode.next; //preNode的next指向indexNode的next preNode.next = indexNode.next; //size 减1 size--; return indexNode.element; } private void rangeIndexCheckForAdd(int index) { if (index > size || index < 0) { //抛出异常 throw new IndexOutOfBoundsException("索引越界,size=" + size + ",index=" + index); } } /** * 返回链表元素的数量 * * @return */ public int size() { return this.size; } /** * 根据索引查找node节点对象 * * @param index * @return */ private Node<T> node(int index) { //检查index是否越界 rangeIndexCheck(index); //定义临时节点引用 Node<T> currentNode = this.head; for (int i = 0; i <= index; i++) { //移动临时节点引用指针，指向下一个节点 currentNode = currentNode.next; } return currentNode; } private void rangeIndexCheck(int index) { if (index >= size || index < 0) { //抛出异常 throw new IndexOutOfBoundsException("索引越界,size=" + size + ",index=" + index); } } /** * 打印数据 */ public void print() { //跳过首节点 Node<T> currentNode = this.head.next; for (int i = 0; i < size; i++) { //打印currentNode节点的数据 System.out.println(currentNode.element); //移动currentNode指向下一个节点 currentNode = currentNode.next; } } } - 测试类
public class MyLinkTest { public static void main(String[] args) { MyLink<String> myLink = new MyLink<>(); myLink.add("Yi"); myLink.add("Jun"); myLink.add("The8"); myLink.add("Carat"); myLink.add("头",0); myLink.add("尾",myLink.size()); System.out.println("数量为：" + myLink.size()); myLink.print(); System.out.println("====删除的元素===="); //删除元素 System.out.println(myLink.remove(0)); System.out.println(myLink.remove(2)); System.out.println(myLink.remove(myLink.size() - 1)); System.out.println("====剩余的元素===="); myLink.print(); } }
4.栈
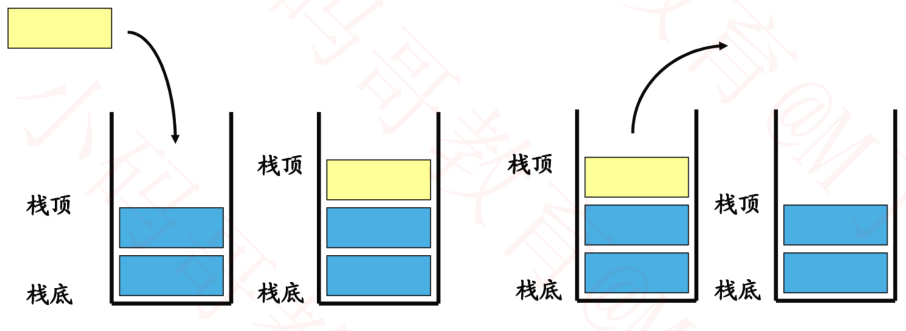
1、栈只允许访问一个数据项：即最后插入的数据项
2、栈提供了一种“后入先出”的一种数据结构
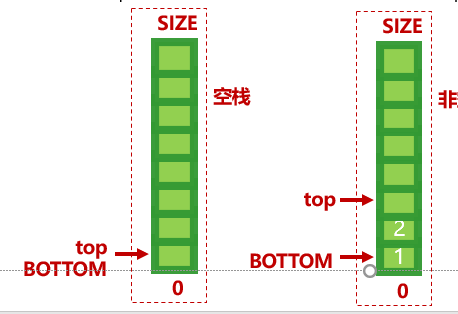
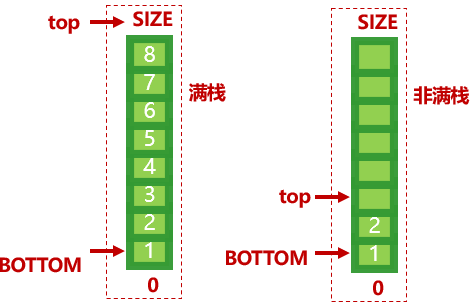
3、栈是一个线性表(物理或逻辑连续的).有两个标识标志出栈的两个端点–栈底和栈顶
4、栈需要提供2个最基本的操作压入 (push) 和弹出 (pop)
- 定义栈
/** * 定义栈，栈只存int值 */ public class MyStack { //容器存储数据(数组) private int[] stack; //压入和弹出时，数组的索引（指针） private int top = 0; //栈大小（创建MyStack对象时候指定） private final int SIZE; //栈底索引值 private final int BOTTOM = 0; /** * 构造方法 * * @param size 栈大小 */ public MyStack(int size) { this.SIZE = size; //new 数组 stack = new int[size]; } /** * 是否满栈 * * @return */ public boolean isFull() { return top == this.SIZE; } /** * 是否为空栈 * * @return */ public boolean isEmpty() { return top == this.BOTTOM; } /** * 压入 * * @param value */ public void push(int value) { if (isFull()) { throw new IllegalStateException("已经满了，不能压入"); } else { //数组[top]=value top++ stack[top] = value; top++; } } /** * 弹出（数据返回并删除） * * @return */ public int pop() { if (isEmpty()) { throw new IllegalStateException("已经空了，不能弹出了"); } else { top--; return stack[top]; } } } - 测试
public class MyStackTest { public static void main(String[] args) { MyStack myStack = new MyStack(8); //压栈 for (int i = 0; i < 8; i++) { myStack.push(i + 1); } System.out.println(myStack.isFull());//true //弹栈 for (int i = 0; i < 8; i++) { System.out.print(myStack.pop() +" ");/*8 7 6 5 4 3 2 1 */ } System.out.println(); System.out.println(myStack.isFull());//false System.out.println(myStack.isEmpty());//true } }
5.队列
1、队列提供了一种“先入先出”的一种数据结构
2、队列也有两个标识标志出两个端点:队头和队尾
3、队列同样要提供2个最基本的操作入队(offer)和出队(poll)
4、循环队列就是反复的利用同一块存储空间进行队列的移动
5、队列的移动主要依靠两个变量来指示,head end
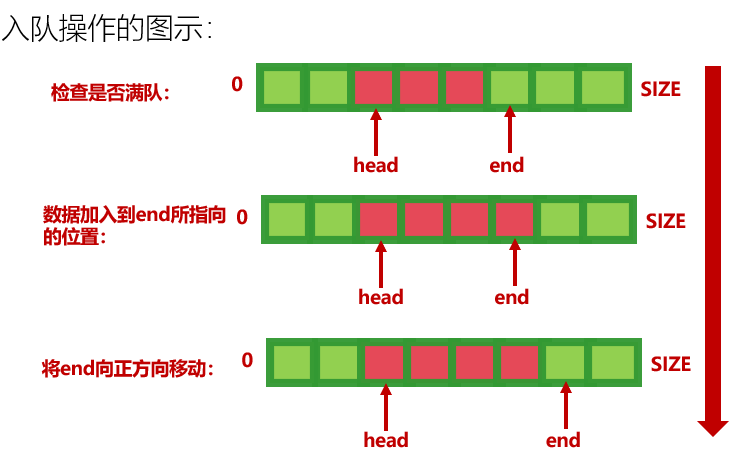
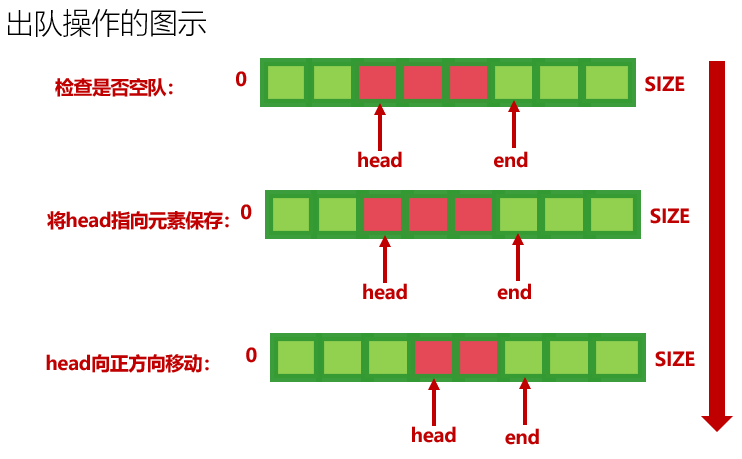
- 定义队列
public class MyQueue { private int head;//队首 private int end;//队尾 private int[] queue;//存储数据的数据 private final int SIZE;//容器大小 public MyQueue(int size) { this.SIZE = size; queue = new int[size]; } /** * 移动索引(移动一步)，用在head和end移动 * * @param index * @return */ private int next(int index) { return (index + 1) % this.SIZE; } /** * 是否满队 * * @return */ public boolean isFull() { return next(this.end) == this.head; } /** * 是否空队 * * @return */ public boolean isEmpty() { return this.head == this.end; } /** * 入队 * * @param value */ public void off(int value) { if (isFull()) { throw new IllegalStateException("满了"); } //赋值 this.queue[this.end] = value; //移动end this.end = next(this.end); } /** * 出队 * * @return */ public int poll() { if (isEmpty()) { throw new IllegalStateException("空了"); } //取值 int result = this.queue[this.head]; //移动head this.head = next(this.head); return result; } } - 测试
public class MyQueueTest { public static void main(String[] args) { MyQueue myQueue = new MyQueue(8); //入队 for (int i = 0; i < 7; i++) { myQueue.off(i + 1); } //出队 for (int i = 0; i < 7; i++) { System.out.print(myQueue.poll() + " "); /*1 2 3 4 5 6 7 */ } } }
6.哈希表
1、存放的数据往往包含两个部分：关键字（Key）作为存储和检索的索引，数据（Data）存放实际的数据项
2、在Hash表中，理想状态下记录在表中的位置和其关键字之间存在着一种确定的关系。这样就能预先知道所查关键字在表中的位置，从而直接通过下标找到记录
3、表中元素和关键字之间的关系由哈希函数确定，即hash（key）=位置
4、由于哈希函数是一个压缩映象，因此，在一般情况下，很容易产生“冲突”现象，即：key1≠key2，而hash(key1)=hash(key2)
5、常见Hash构造函数的方法：
-
直接定址法 ；数字分析法；平方取中法；折叠法；除留余数法；随机数法
6、“处理冲突”的实际含义是：为产生冲突的关键字寻找下一个哈希地址，包括开放定址法、再哈希法、链地址法等，链地址法被很多语言的Hash表默认实现所选择：
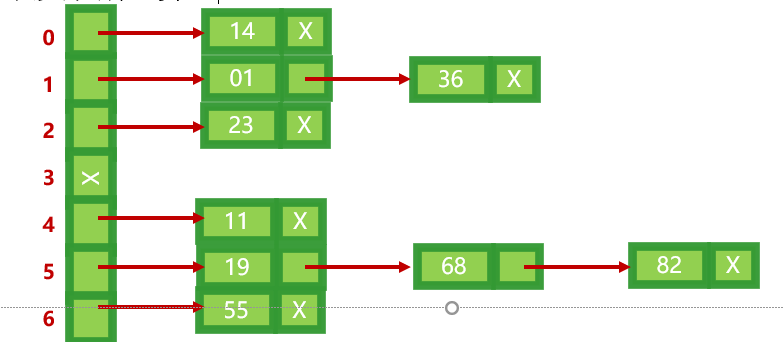
7、装载因子就是hash表中已经存储的关键字个数，与可以散列位置的比值，表征着hash表中的拥挤情况，一般而言，该值越大则越容易发生冲突。
