3) Some Lower Bounds
防盗 https://www.cnblogs.com/setdong/p/17549887.html
来自 Chapter 3.4 of Foundations of machine learning
1. Lemma statement
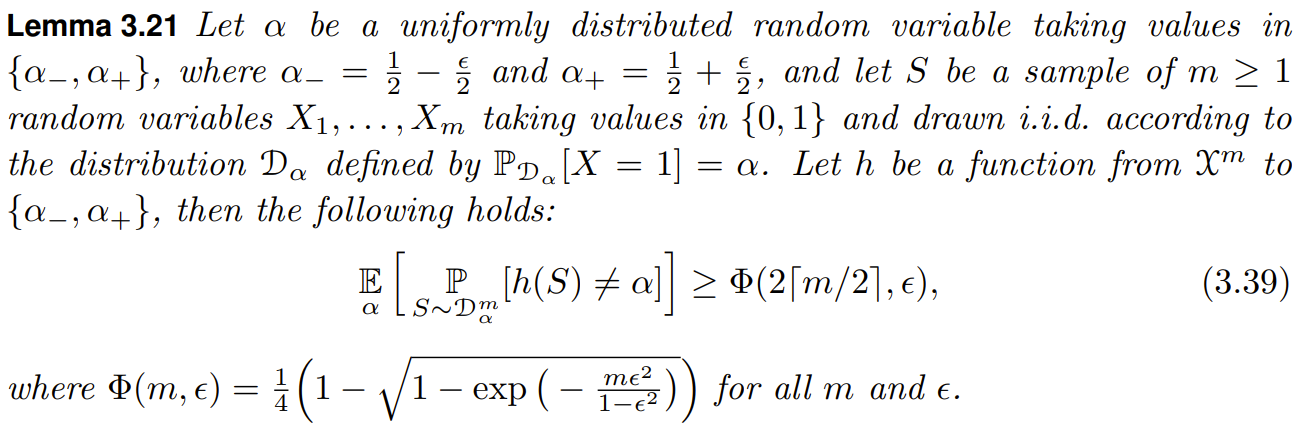
首先理解定理在讲什么: 随机变量 \(\alpha\) 的取值为 \(\alpha_{-}\) 或 \(\alpha_{+}\) 且服从均匀分布. 分布 \(D_{\alpha}\) 是与 \(\alpha\) 的值有关的一个分布. 现在从分布 \(D_{\alpha}\) 采样 \(m\) 个点, 记为 \(S=\{X_1,...,X_m\}\). \(h\) 是一个函数, 它的输入是 \(S\), 输出是 \(\alpha_{-}\) 或 \(\alpha_{+}\), 也就是说 \(h\) 接收采样得到的 \(m\) 个样本点, 然后预测采样的分布是 \(D_{\alpha_-}\) 还是 \(D_{\alpha_+}\).
不等式 (3.39) 给出了 \(h\) 的错误率的下界, 这个下界受样本量 \(m\) 和 \(\alpha_{-}\) 与 \(\alpha_{+}\) 之间的差 \(\epsilon\) 影响.
2. 证明
考虑有两个不均匀的硬币(0 表示反面, 1 表示正面):
- 硬币 \(x_A\): \(\Pr[x_A=0]=\alpha_-\)
- 硬币 \(x_B\): \(\Pr[x_B=0]=\alpha_+\)
以相同概率随机地选一个硬币 \(x\in\{x_A, x_B\}\), 投掷 \(m\) 次, 记录正反, 这样可以得到一个由 0, 1 组成的, 大小为 \(m\) 的序列, 也就是定理中的 \(S\). 然后根据这个序列 \(S\) 预测一开始选择的硬币是哪个.
最好的决策方法是: \(f_0: \{0,1\}^m \rightarrow \{x_A, x_B\}, f_0=x_A\) iif (当且仅当) \(N(S)< m/2\), 其中 \(N(S)\) 是 \(S\) 中 0 的个数. 接下来推算 \(f_0\) 错误率的下界, 然后证明 \(f_0\) 是最好的决策方法.
接下来需要用到两个 lower bound 定理, Binomial distribution tails 和 Normal distribution tails (忽略证明):
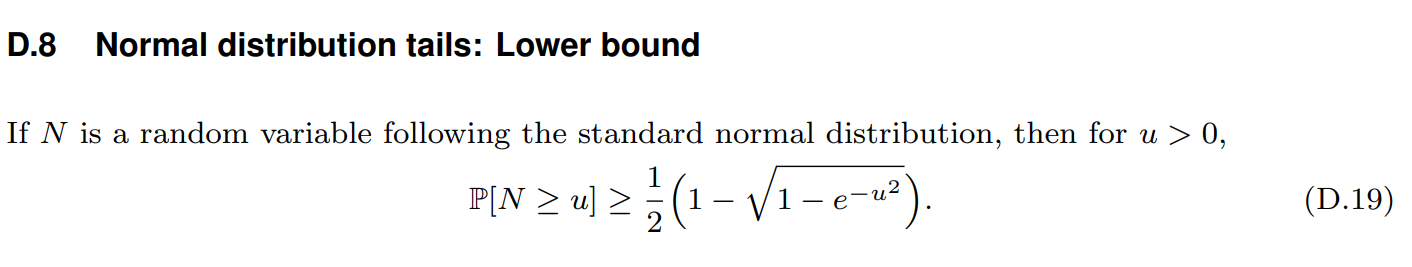
所以 \(\Pr[N(S)< m/2|x=x_B]=\Pr[B(m,p)\geq k]\), 其中 \(k=m/2\)(当 \(m\) 是偶数), \(k=\left \lceil m \right \rceil/2\)(当 \(m\) 是奇数), \(p=\alpha_-\), 利用 (D.8) 和 (D.19) 的结论就证明完毕了.
证明没有比 \(f_0\) 更好的决策方法:
\(f:\{0,1\}^m\rightarrow \{x_A, x_B\}\) 表示任意决策方法, \(F_A\) 表示满足 \(f(S)=x_A\) 的样本集\(S\)的集合, \(F_B\) 表示其补集.
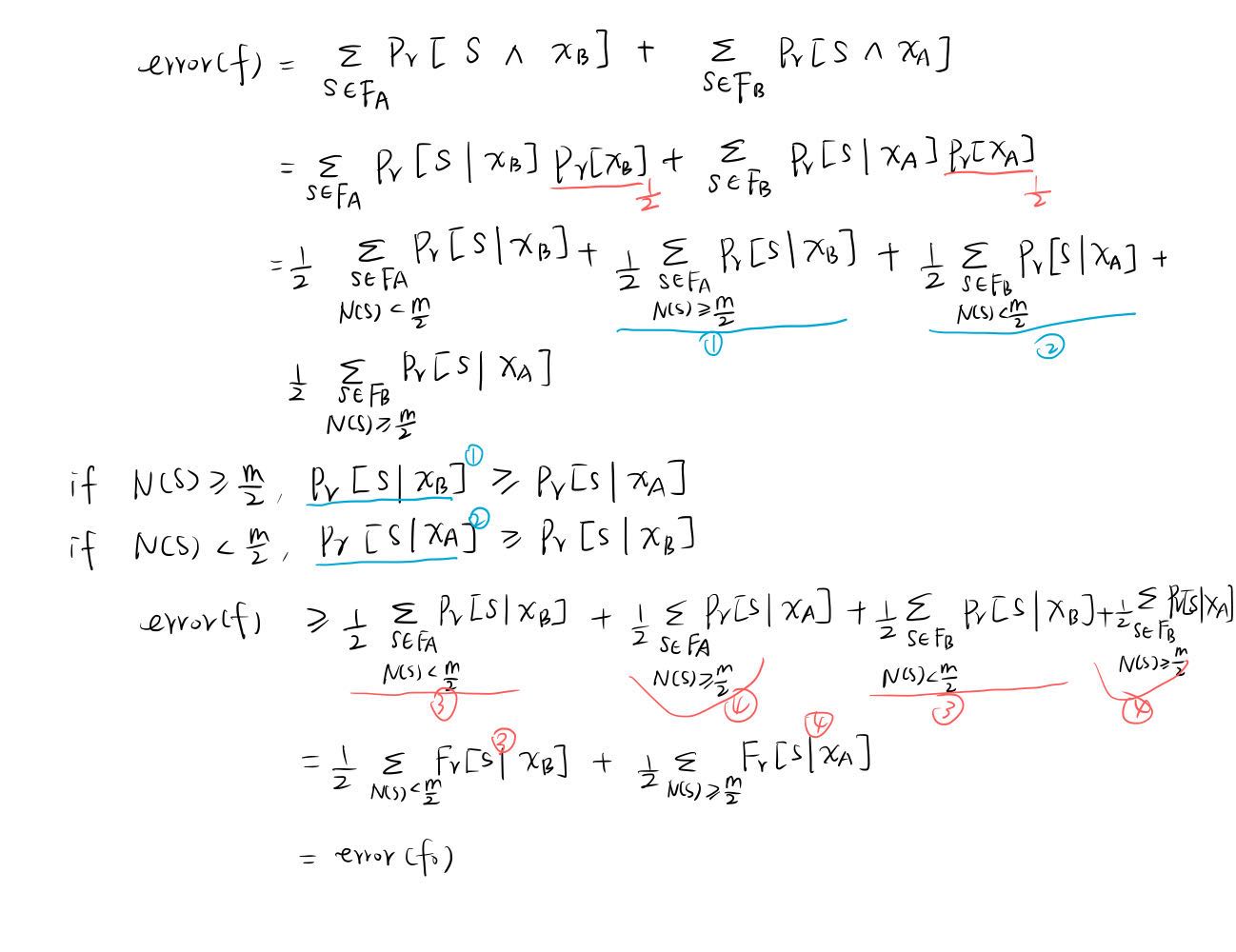
打公式太难了
上图推导的结论是: 任意 \(f\) 的错误率 \(\geq\) \(f_0\) 的错误率, 所以 \(f_0\) 是最好的.
本文提到的所有的错误率都指的是: Generalization error/ true error/ risk
