对抗攻击方法BIM与PGD的区别

Basic iterative method(BIM):论文地址 笔记地址

Projected gradient descent(PGD):论文地址 笔记地址

区别1

来自于：https://www.sciencedirect.com/science/article/pii/S209580991930503X
1）BIM 将一步的FGSM直接扩展为多步方法：

\[x'_{t+1}=Clip_{x, \epsilon} \{x'_{t}+\alpha\; {\rm sign}(\bigtriangledown_{x}J(\theta,x'_{t}, y))\} \tag{1} \]

BIM 每次迭代以很小的步长执行FGSM，将对抗样本剪裁和更新到一个合法的范围内；迭代 \(T\) 次，\(\alpha T = \epsilon\)，\(\alpha\) 是每次迭代中扰动的大小。

2）PGD是FGSM的多步变体：

\[x'_{t+1} = \Pi _{x+\mathcal{S}} \left ( x'_{t}+\alpha \;{\rm sign}(\bigtriangledown_x J(\theta,x'_{t}, y)) \right ) \tag{2} \]

为了约束对抗扰动的大小，PGD 不使用 \(\alpha T = \epsilon\)的方式，而是将对抗性样本投影到 \(x\) 的 \(l_\infty\)-ball(\(\epsilon-l_\infty\) neighbor) 中，因此扰动的值大于 BIM 的扰动。公式（2）中的 \(\mathcal{S} \subseteq \mathbb{R}^d\) 为扰动集合。

区别2

来自于：https://github.com/MadryLab/mnist_challenge/issues/3

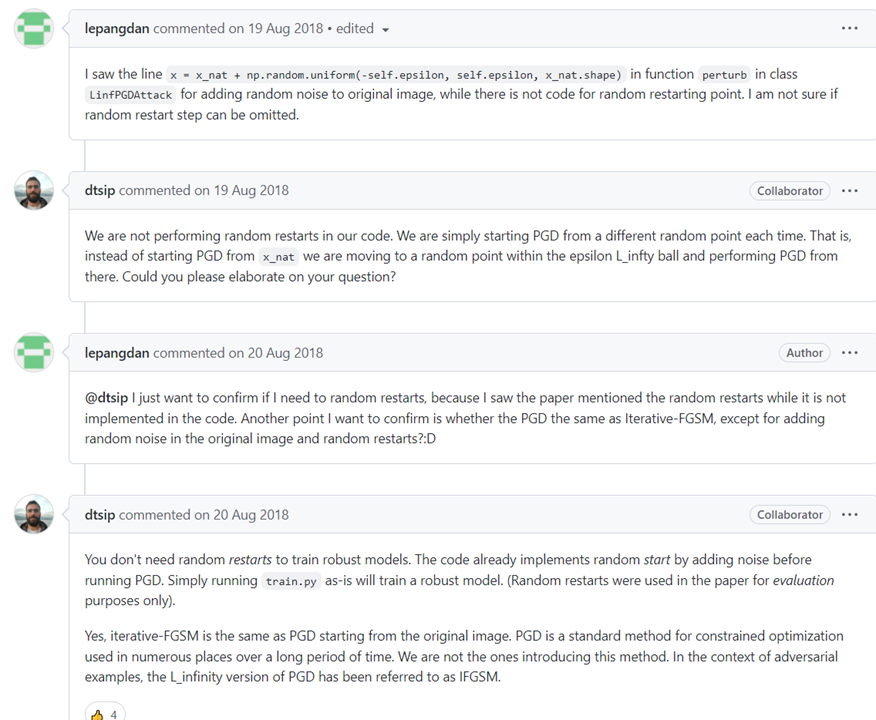
• PGD添加了一个均匀分布的随机噪声作为初始化（随机初始扰动），也就是：选择 \(x\) 的 \(\epsilon-l_\infty\)- ball 内的一个随机点作为起始点，从这个点开始执行 PGD。