【论文笔记】(模型压缩)Do Deep Nets Really Need to be Deep?
摘要
作者通过模型压缩(model compression)使浅层的网络学习与深层网络相同的函数,以达到深层网络的准确率(accuracy)。当与深浅模型的参数量相同时,浅层模型可以高保真地模仿具深层网络,这说明了深层网络学到的函数并不一定很深。
2 训练浅层网以模仿深层网络
2.1 Model Compression
模型压缩是训练一个小型模型来近似一个大型模型表达的函数,方法是将unlabeded的数据传递到精准的大型模型,收集该模型产生的分数,然后综合以上内容产生新的labels,使用这些综合labels的数据来训练小型模型。如果小型模型完美地模仿大型模型,它会做出与复杂模型完全相同的预测和错误,但这通常无法做到。
2.2 Mimic Learning via Regressing Logit with L2 Loss
数据集为TIMIT和CIFAR-10,首先使用这些原始数据训练深层网络,激活层使用softmax,softmax输出的值为probability,即 \(p\) 值(\(p_k = e^{z_k}/\sum_j e^{z_j}\)),softmax的前一层为logits层(\({\rm logit}(p)=\ln \left(\frac{p}{1-p}\right)\) 可以将\((0,1)\)的值映射到\(\pm \infty\)),logits的输出/softmax的输入记为 \(z\) 值;损失函数为交叉熵。
然后使用\(z\)值作为标签来训练浅层网络,而非使用\(p\)值,因为使用logit值进行训练可以捕获更多的不明显的信息,避免信息丢失,更好的学习深层模型的内部。
将 SNN-MIMIC 学习的目标函数表述为 给定训练数据 \(\{(x^{(1)},z^{(1)}),...,(x^{(T)},z^{(T)})\}\) 的回归问题:
\(W\) 是输入特征和隐藏层之间的权重矩阵,\(\beta\) 是从隐藏层到输出单元的权重,\(g(x^{(t)};W,\beta)=\beta f(Wx^{(t)})\) 是模型在第\(t\)个训练数据点上的预测,\(f(\cdot)\) 是激活。参数 \(W\) 和 \(\beta\) 通过标准常规的BP和SGD不断更新。
2.3 Speeding-up Mimic Learning by Introducing a Linear Layer
浅层网络必须在单层中具有更多的非线性隐藏单元才可以匹配深层网络的参数,但是这样的结构导致学习非常缓慢,因为\(W\)很大且含有很多高度相关的参数,这导致了尽管最终浅层网络能够学习到准确的函数,但是梯度下降收敛的十分缓慢(数周,即使使用GPU)。
在输入层和非线性隐藏层之间引入一个具有 \(k\) 个线性隐藏单元的线性层可以显着加快学习速度:将\(W\in \mathbb{R}^{H \times D}\) 分解为两个低秩矩阵的乘积 \(U \in \mathbb{R}^{H \times k}\) 和 \(V \in \mathbb{R}^{k \times D}\),其中 \(k \ll D,H\)。新的损失函数可为:
权重\(U,V\)可以通过线性层的反向传播来学习。这种对权重矩阵 \(W\) 的重参数化不仅提高了收敛速度,还将存储空间从 \(O(HD)\) 减少到 \(O(k(H + D))\)。
3 TIMIT Phoneme Recognition(实验1)
3.1 Deep Learning on TIMIT
作者选择三个模型进行训练,第一个是DNN,包含三个全连接前馈隐藏层,每层包括2000个带ReLU的线性单元;第二个是CNN,包含一个卷积层,三个隐藏层(同DNN的配置),后接一个max-pooling层;第三个为ECNN,是由9个 CNN 融合成的ensemble。
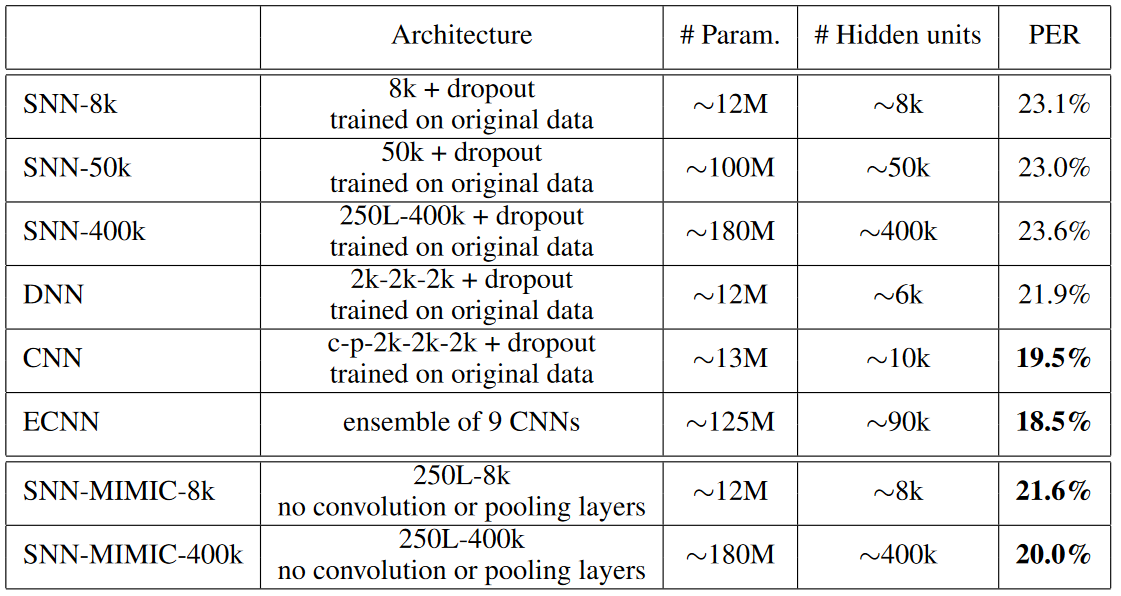
表1. 深浅网络的对比:TIMIT 测试集上的音素错误率(Phone Error Rate,PER)。
如表 1,最上三个网络为分别具有 8000、50k 、400k 个隐藏单元的浅层神经网络,尽管这些浅层网络的参数量是DNN、CNN、ECNN的十倍,但它们的准确率却低于深层网络。
3.2 Learning to Mimic an Ensemble of Deep Convolutional TIMIT Models
可看出,在这六个模型中ECNN的效果最好,所以选择ECNN作为教师模型,如 2.2 节所述,ECNN中的每个CNN都含有logits,将它们的logits平均以用于浅层网络的训练。
学生模型为分别含有 8k (SNN-MIMIC-8k) 和 400k (SNN-MIMIC-400k)个ReLUs隐藏单元的浅层网络。 如 2.3 节所述,两个模型在输入和非线性隐藏层之间都有 250 个线性单元以加快学习速度。
3.3 Compression Results for TIMIT
表1. 的后两行为浅层网络的准确度,它们通过模型压缩训练以模拟 ECNN。可以看到,具有一个隐藏层的神经网络 (SNN-MIMIC-8k) 可以被训练为与具有相似数量参数的 DNN 一样好。此外,如果将浅层网络中的隐藏单元数量从 8k 增加到 400k,具有一个隐藏层的神经网络 (SNN-MIMIC-400k) 可以被训练得与CNN相当的性能,即使 SNN-MIMIC-400k 网络没有卷积层或池化层。
4 Object Recognition: CIFAR-10(实验2)
4.1 Learning to Mimic a Deep Convolutional Neural Network
采用与 TIMIT 实验相同的方法:使用一组深度 CNN 模型来标记 CIFAR-10 图像以进行模型压缩。
非卷积网络无论其深度如何,都在 CIFAR-10 上表现不佳,所以在浅层模型中引入单层卷积和赤化作为特征提取器,同时保持模型尽可能的浅。因此,SNN-MIMIC 模型包括一个卷积和最大池化层,然后是完全连接的 1200 个线性单元和 30k 个非线性单元。同样地,线性单元只是为了加速学习。
Results
如表2,浅层网络达到了与有多个卷积和池化层的 CNN 相当的精度。 尽管深度卷积网络比浅层网络具有更多的隐藏单元,但由于权重共享,前者比后者具有更少的参数。值得注意的是,随着教师模型性能的提高,浅层模型的准确性继续提高。
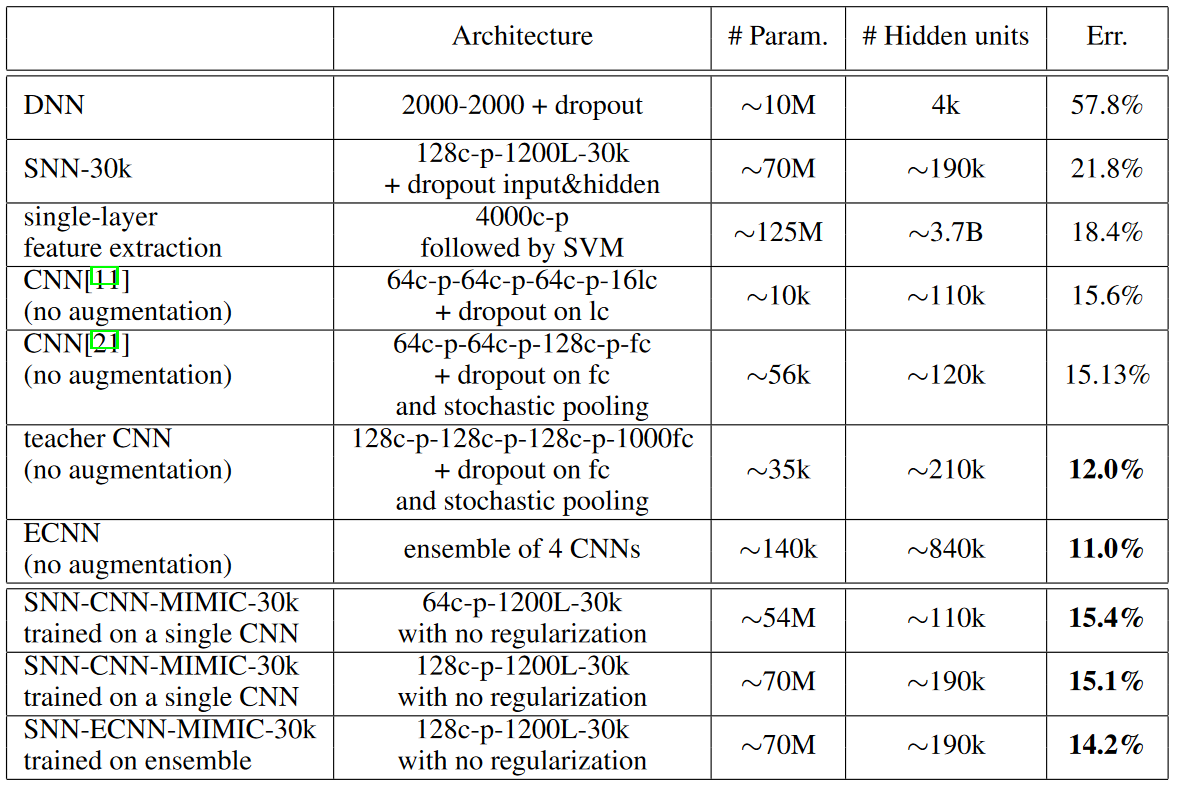
表2. 深浅网络的对比:CIFAR-10 上的分类错误率。 c代表卷积层; p代表池化层; lc代表局部连接层; fc代表全连接层。
5 Discussion
5.1 Why Mimic Models Can Be More Accurate than Training on Original Labels
以上两个实验可以看出,在从其他模型中提取的预测目标上训练的模型可能比在原始标签上训练的模型更准确。原因有:
- 如果某些标签有错误,教师模型可能会消除其中一些错误(即审查数据),从而使学生模型更容易学习
- 如果\(p(y|x)\)中存在复杂区域,特征和样本密度难以学习,教师模型会过滤目标,数据集中的复杂性被冲走。教师网络为学生提供了更简单、更软的标签。
- 学习原始的硬标签(0/1)可能比学习从教师模型输出的条件概率更困难,教师模型的不确定性比原始 0/1 标签更能指导学生模型。通过对 logits 的训练,这种好处似乎得到了进一步的增强。
通过实验,作者认为上述机制可以看作是有助于防止学生模型过度拟合的正则化形式。在原始目标上训练的浅层模型比深层模型更容易过度拟合,如果对浅层模型添加正则化,它与深层模型之间的一些性能差距可能会消失。模型压缩似乎是一种正则化形式,可有效减少这种差距(猜想+实验得到的结论)。
5.2 The Capacity and Representational Power of Shallow Models
实验表明,随着教师模型准确性的提高,学生模型的准确性继续提高。在对相同目标进行训练时,SNN-MIMIC-8k 的性能总是比参数多 10 倍的 SNN-MIMIC-160K 差。
虽然由于大小的不同,两个模型之间存在一致的性能差距,但较小的浅层模型最终能够通过向更好的老师学习,达到与较大的浅层网络相当的性能,并且两个模型的准确率继续随着教师准确性的提高而提高。
这表明,如果有更准确的教师模型和/或更多未标记的数据,具有与深度模型相同参数的浅层模型可能能够学习更准确的函数。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号