【论文笔记】（2017，BIM）Adversarial Machine Learning at Scale

本文主要是给出了两类多个对抗攻击方法：one-step 攻击和 multi-step 攻击，并在大型模型和大型数据集上对这些方法进行对比实验，实验结果发现使用 one-step 样本进行对抗训练的模型具有较强的对抗鲁棒性，且 one-step 攻击比 multi-step 攻击的可转移性强，此外还发现了标签泄露（label leaking）实验结果的详细分析在这篇博客中。

1 介绍

本文的主要贡献：

• 在ImageNet上，对Inception v3模型进行对抗训练，显着提高了模型的对抗鲁棒性（FGSM和其他one-step方法生成的对抗样本）。
• 证明了不同类型的对抗样本在模型之间往往具有不同的可迁移性（transferability）。
• 发现模型容量（即参数量）大的模型往往更具对抗鲁棒性。
• 发现了"标签泄漏"。

2 生成对抗样本的方法

2.1 术语和符号

1. \(X\)：干净样本；
2. \(X^{adv}\)：对抗样本；
3. 错误分类的对抗样本：被神经网络错误分类的对抗样本；
4. \(\epsilon\)：对抗性扰动的大小；
5. \(J(X,y_{true})\)：损失函数；
6. \(Clip_{X, \epsilon}(A)\)表示按元素裁剪\(A\)，其中\(A_{i,j}\)被裁剪到；\([X_{i,j}-\epsilon, X_{i,j}+\epsilon]\)范围内；
7. one-step方法是指在计算一次梯度后生成对抗样本；迭代（iterative）方法则是多次梯度的更新。

2.2 攻击方法

这节给出了4个攻击方法，前两个为 one-step，后两个为 multi-step，但文章的附录又给出了其他的 one-step 方法用于实验请看这篇博客：

• Fast gradient sign method（FGSM）为本文作者在这篇论文中提出的著名方法：

  \[X^{adv}=X+\epsilon\;{\rm sign}(\bigtriangledown_{X}J(X, y_{true})) \tag{1} \]

  与L-BFGS（本文作者在首次提出对抗样本的论文中提出的方法）等更复杂的方法相比，这种方法简单且计算效率高，但通常成功率较低。在ImageNet上，对于 \(\epsilon\in[2, 32]\)，FGSM生成的对抗样本的top-1错误率约为63%-69%。

• One-step target class methods 作者对FGSM做出了改进：最大化某个特定目标类别 \(y_{target}\) 的概率 \(p(y_{target}|X)\)，其中\(y_{target}\)是给定图像的"最不可能"的类。对于使用交叉熵损失的神经网络，one-step方法的公式为：

  \[X^{adv}=X-\epsilon\;{\rm sign}(\bigtriangledown_{X}J(X, y_{target})) \tag{2} \]

  作为目标类，可以使用由网络 \(y_{LL} = \arg \min_{y} \{p(y | X)\}\) 预测的最不可能的类。将此方法记为"step l.l."。 也可使用随机类作为目标类，此时将此方法记为"step rnd."。

• Basic iterative method（BIM）是FGSM的一个直接扩展，将一步改为多步，步长很小：

  \[X^{adv}_{0}=X, \;\; X^{adv}_{N+1}=Clip_{X, \epsilon} \{X^{adv}_{N}+\alpha\; {\rm sign}(\bigtriangledown_{X}J(X^{adv}_{N}, y_{true}))\} \]

  在实验中作者将\(\alpha\)设为1，即在每一步仅将每个像素的值更改1，迭代次数设为\(\min (\epsilon+4, 1.25\epsilon)\)。将此方法记为"iter. basic"。

• Iterative least-likely class method 以迭代的方式运行"step l.l."方法，此时可以得到在超过 99% 的情况下被错误分类的对抗样本：

  \[X^{adv}_{0}=X, \;\; X^{adv}_{N+1}=Clip_{X, \epsilon} \{X^{adv}_{N}-\alpha\; {\rm sign}(\bigtriangledown_{X}J(X^{adv}_{N}, y_{LL}))\} \]

  \(\alpha\)和迭代次数的设置与"iter. basic"的相同。将此方法记为"iter. l.l."。

3 对抗训练

对抗训练的基本思想是将对抗样本加到训练集中，并在训练的每一步不断生成新的对抗样本。 由于本文选择大型数据集ImageNet进行对抗训练，作者使用批标准化(Batch Normalization)，对此，在进行每个训练步骤之前，需要将样本分为包含正常样本和包含对抗样本的batch，如下面的算法1。

损失函数为：

\[Loss=\frac{1}{(m-k)+\lambda k}\left (\sum_{i \in CLEAN} L(X_i|y_i)+\lambda \sum_{i \in ADV}L(X_i^{adv}|y_i)\right) \]

其中\(L(X|y)\)是单个样本\(X\)（它的真实类别为\(y\)）的损失，\(m\)是minibatch 中训练样本的总数，\(k\)是minibatch中对抗样本的数量，\(\lambda\)是控制损失中对抗样本的相对权重的参数。可以看出，此损失可以独立控制每个batch中对抗样本的数量和相对权重。

作者选择\(\lambda=0.3\)，\(m=32\)，\(k=16\)进行实验。从算法1中可以看出，在训练用到的minibatch中，\(k\)个干净样本被替换为其对应的对抗样本，其余干净样本不变。

作者对比了此论文采用的对抗训练方法，他们选择的数据集规模较小（MNIST 和 CIFAR-10），他们用对抗样本替换了整个minibatch，此时的对抗训练不会导致干净样本的准确率降低。但是对于本文选择的大规模数据集ImageNet，作者通发现本文中用的方法效果更佳。

作者发现，如果训练期间固定\(\epsilon\)，那么网络只会对\(\epsilon\)d的特定值鲁棒。因此，作者建议为每个训练样本独立地随机选择\(\epsilon\)。在实验中，当\(\epsilon\)从一个由\([0, 16]\)定义的截断正态分布truncated normal distribution）中提取时实验的结果最好，其基本正态分布为\(N(\mu=0, \sigma=8)\)。

4 实验

作者选择ImageNet数据集和Inception v3模型进行对抗训练，其中minibatch为32，迭代次数为\(150k\)，使用 RMSProp 优化器，学习率为 0.045。

作者研究了对抗训练和其他正则化（dropout、标签平滑和权重衰减）的相互作用，发现：禁用标签平滑和/或dropout会导致干净样本的准确率小幅下降和对抗样本的准确率小幅上升。另一方面，减少权重衰减会导致干净样本和对抗样本的准确率都降低。

作者还选择N次延迟（delay）对抗训练，即前N次迭代只使用干净样本进行训练，N次之后，在minibatch中选择3章中描述的样本（既包含干净又包含对抗），作者选择令N=10k。

作为评估，作者选择ImageNet 验证集，该验证集包含 50,000 张图像，并且与训练集不相交。

4.1 对抗训练的结果

首先在对抗训练中比较不同的one-step方法。

在实验中，对抗训练导致干净样本的准确率略有下降，这与先前的研究不同，之前的研究结论为对抗训练能提高测试集的准确率。对此，一种可能的解释是对抗训练起到了正则化的作用；对于ImageNet这样的数据集，最先进的模型通常具有较高的训练集误差，使用像对抗训练这样的正则化器会增加训练集误差，而不是减少the gap between训练集误差和测试集误差。
实验结果表明，对抗性训练应该在两种情况下使用：

1. 当模型过拟合，需要正则化器时。
2. 当对抗样本的安全性是一个问题时。

实验发现：使用"step l.l."或"step rnd."方法能在测试集上获得最好的结果，作者最终选择"step l.l."进行实验。

使用"step l.l."进行对抗训练的结果见表1，可以看出：

• 对抗样本的top1和top5的准确率得到显著提高（分别高达 74% 和 92%），使其与干净样本的准确率很接近。 然而，干净样本却损失了大约 0.8% 的准确率。
• 稍微增加模型的size能够稍微减少干净样本的准确性差距（没懂）。

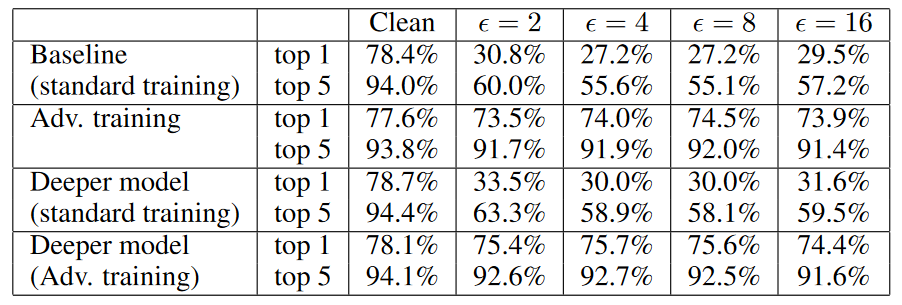
表1. 经过对抗训练的网络在干净样本和对抗样本（with various \(\epsilon\)）上的top1 和 top5 准确率的对比。其中，训练和评估都使用的"step l.l."方法。对抗训练导致baseline模型更具对抗鲁棒性，但在干净样本上降低了一些准确率。因此，使用两个额外的 Inception 块训练了一个deeper model，deeper model通过对抗训练获得了更高的对抗鲁棒性，并且在干净样本上损失的准确率比较小的模型要少。

接下来研究迭代/多步方法。

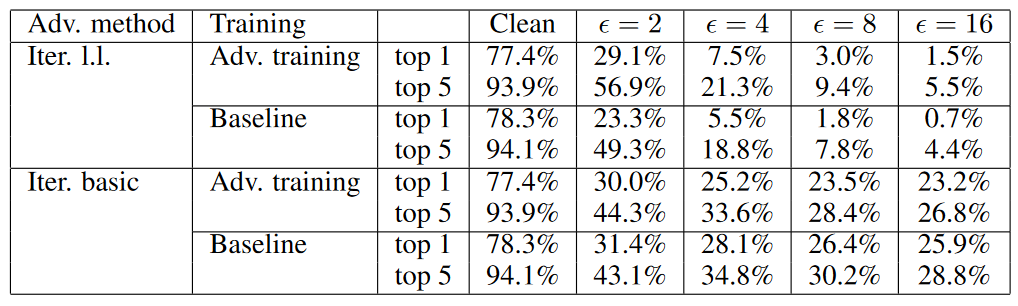
表2. 对抗训练网络在迭代对抗样本上的准确率。对抗训练是采用"step l.l."方法，结果是在 140k 次迭代训练后计算的，可以看到使用one-step对抗样本进行对抗训练不会增加对迭代对抗样本的鲁棒性。

作者尝试在训练期间使用迭代对抗样本，但是计算成本很高，且效果也不好。

4.2 标签泄露 label leaking

当一个模型在 FGSM 对抗样本上进行训练，然后使用 FGSM 对抗样本进行评估时，对抗样本的准确率远高于干净样本的准确率（见表 3）。当使用其他one-step方法时也会出现这种现象（但程度较轻）。

表3. 标签泄露对对抗样本的影响。当使用 FGSM 进行训练和评估时，对抗样本的准确率高于干净样本。当使用"step l.l."进行训练和评估时，这种效果不会发生。在这两个实验中，训练都进行了 150k 次迭代，初始学习率为 0.0225。

作者认为：特定样本的标签已经泄露\(\Leftrightarrow\)(当且仅当)模型正确地分类了一个对抗样本，该对抗样本是使用真实标签生成的，但错误分类了相应的对抗样本，而该对抗样本的生成不使用真是标签。

作者对此的解释为：one-step methods that use the true label perform a very simple and predictable transformation that the model can learn to recognize. 在对抗样本构建过程中，无意将有关真实标签的信息泄漏到输入中。如果选择不使用真实标签构建的对抗样本，此效应就会消失。如果使用迭代方法，该效应也会消失，这可能是因为迭代过程的输出比one-step过程的输出更多样化且更难以预测。

所以，作者不建议使用 FGSM 或那些使用真实类标签的方法来评估对抗样本的鲁棒性；建议使用其他不直接访问标签的one-step法。

4.3 模型容量对对抗鲁棒性的影响

鲁棒性随着模型大小的增加而不断增加。

4.4 对抗样本的可迁移性

实验结果为：FGSM 对抗样本是可转移性最强，而"iter l.l."最差；另外，"iter l.l."方法能够在超过 99% 的情况下欺骗模型，而 FGSM 欺骗网络的可能性最小。

这表明：特定方法的可转移性与该方法欺骗网络的能力之间可能存在反比关系。一种可能的解释可能是迭代方法往往过度拟合网络参数。