【凸优化】2 超平面，半空间，欧氏球，椭球，范数球，范数锥

1 超平面 Hyperplanes

定义：超平面是一个形式为\(\{x|a^Tx=b\}\)的集合，其中\(a\in \mathbb{R}^n, a \neq 0, b\in \mathbb{R}\)。
分析上讲，超平面是线性方程的非零解集；几何上讲，超平面是与向量\(a\)具有恒定内积的点集，或具有法向量\(a\)的超平面，常数\(b\)决定了超平面与原点的偏移量。

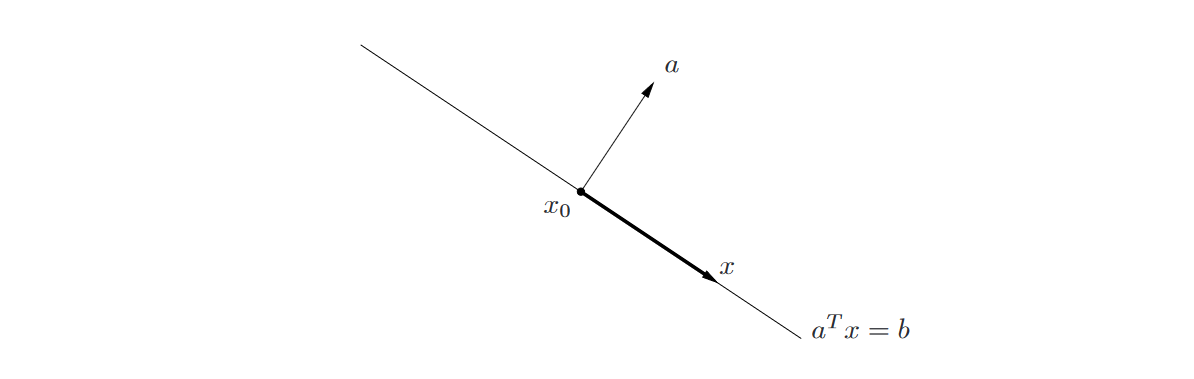
图1. \(\mathbb{R}^2\)中的超平面，法向量为\(a\)，点\(x_0\)在超平面内。在超平面中的任意一点\(x\)，\(x-x_0\)（图中加粗的向量）与\(a\)正交。

超平面也可表示为\(\{x|a^T(x-x_0)=0\}\)，其中\(x_0\)是超平面中的任意一点；
也可表示为\(\{x|a^T(x-x_0)=0\}=x_0+a^\perp\)，其中\(a^\perp\)表示\(a\)的正交补集。可以看出，超平面由偏移量\(x_0\)和与法向量\(a\)正交的全部向量组成，如图1。

2 半空间 Halfspaces

上述的超平面能够将\(\mathbb{R}^n\)划分成两个半空间，半空间是一个形式为\(\{x|a^Tx \leq b\}\)的集合，其中\(a\neq 0\)，也是一个线性不等式的非零解集。

半空间是凸集，不是仿射集，如图2。

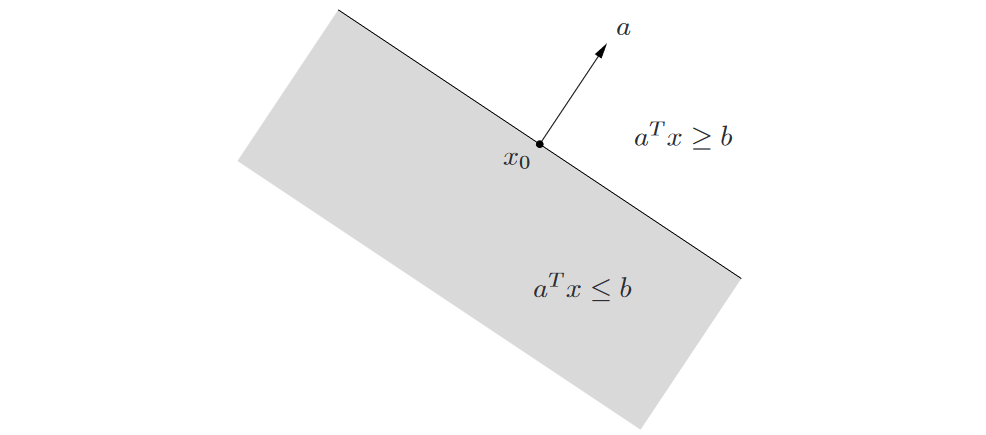
图2. 超平面\(a^Tx=b\) 将\(\mathbb{R}^n\)划分成两个半空间。由\(a^T x \geq b\) 确定的半空间(未加阴影)是沿\(a\)方向延伸的。 由\(a^T x \leq b\) 确定的半空间(阴影部分)在\(-a\)方向上延伸的。向量\(a\)是这个半空间的外法线。

半空间也可表示为\(\{x|a^T(x-x_0)\leq0\}\)，其中\(x_0\)是对应的超平面上的任意点，即满足\(a^T x_0 = b\)。
对此的几何解释为：半空间由\(x_0\)和任何与向量\(a\)(\(a\)为向外的法向量)成钝角或直角的向量组成。如图3。

图3. 由\(a^T(x-x_0)\leq0\)定义的半空间（阴影部分）：向量\(x_1 - x_0\)与\(a\)成锐角，因此\(x_1\)不在半空间中。 向量 \(x_2 - x_0\) 与 \(a\) 成钝角，在半空间中。

集合\(\{x|a^Tx <b\}\)称为开半空间(open halfspace)。

3 欧式球 Euclidean Balls

在\(\mathbb{R}^n\) 空间中的球/欧几里得球的形式为：

\[B(x_c,r)=\{x|\; ||x-x_c||_2 \leq r\}=\{x|\; (x-x_c)^T(x-x_c)\leq r^2\} \]

其中\(r>0\)，\(||\cdot||_2\)为欧几里德范数（即\(L_2\)范数），\(x_c\)是球的中心，标量\(r\)为半径，\(B(x_c,r)\)由距中心\(x_c\)距离小于等于\(r\)的所有点组成，即球表面和球内部。
球的另一种表示形式为：

\[B(x_c,r)=\{x_c + ru|\; ||u||_2 \leq 1\} \]

球是一个凸集，证明如下：
球内（这里的球内指在球内部或球表面，并非单指内部）任取两点\(x_1, x_2\)，根据性质可知\(||x_1-x_c||_2 \leq r\) 和 \(||x_2-x_c||_2 \leq r\)，假设 \(\theta \in [0,1]\)，则根据凸集的定义，我们想要知道线段\(\theta x_1 + (1-\theta) x_2\) 是否在球内：

\[||\theta x_1 + (1-\theta) x_2 - x_c||_2 = ||\theta(x_1-x_c) + (1-\theta) (x_2-x_c)||_2 \\ \leq \theta||x_1-x_c||_2 + (1-\theta) ||x_2-x_c||_2 \leq r\]

4 椭球 Ellipsoids

另一个凸集类的集合为椭球，其形式为：

\[\varepsilon = \{x|(x-x_c)^T P^{-1}(x-x_c)\leq 1\} \]

其中\(P=P^T\succ 0\)，即\(P\)为对称且正定的矩阵(正定：对任意\(x\neq 0\)，有 \(x^T P x>0\))。同样的，\(x_c\in \mathbb{R}^n\) 为椭球的中心，\(P\) 决定了椭球在每个方向上从\(x_c\)延伸多远，\(\varepsilon\)的半轴长度由\(P\)的特征值\(\sqrt{\lambda_i}\)给出。

当\(P=r^2 I\)时，上述公式的椭球就是球。

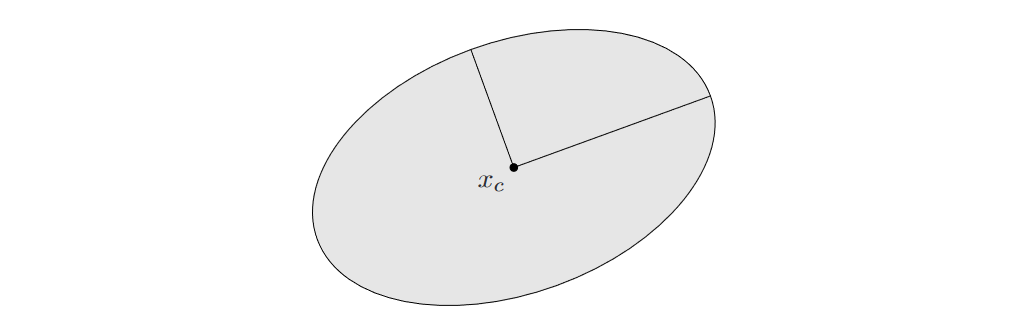
图4. 二维空间中的椭球（也是椭圆），\(x_c\)为中心，两个线段为半轴。

椭球的另一个表达式为：

\[\varepsilon =\{x_c + A\mu| \; ||\mu||_2\leq 1\} \]

其中\(A\)是非奇异的方阵。这个公式中的集合称为退化椭球（degenerate ellipsoids），它的仿射维数等于\(A\)的秩，退化椭球也是凸的。

5 范数球 Norm Balls

当将欧氏球公式中的二范数（\(||\cdot||_2\)）换成\(\mathbb{R}^n\)上的任意范数（\(||\cdot||\)），此时的集合称为范数球：

\[B(x_c,r)=\{x|\; ||x-x_c||\leq r\} \]

同样的，\(r\)为半径，\(x_c\)为中心，范数球为凸集。

6 范数锥 Norm Cones

范数锥的公式为：

\[C=\{(x,t)|\; ||x||\leq t\} \]

其中，\(x\in \mathbb{R}^n\)，\(t\)，故\(C \subseteq \mathbb{R}^{n+1}\)，且为凸锥。

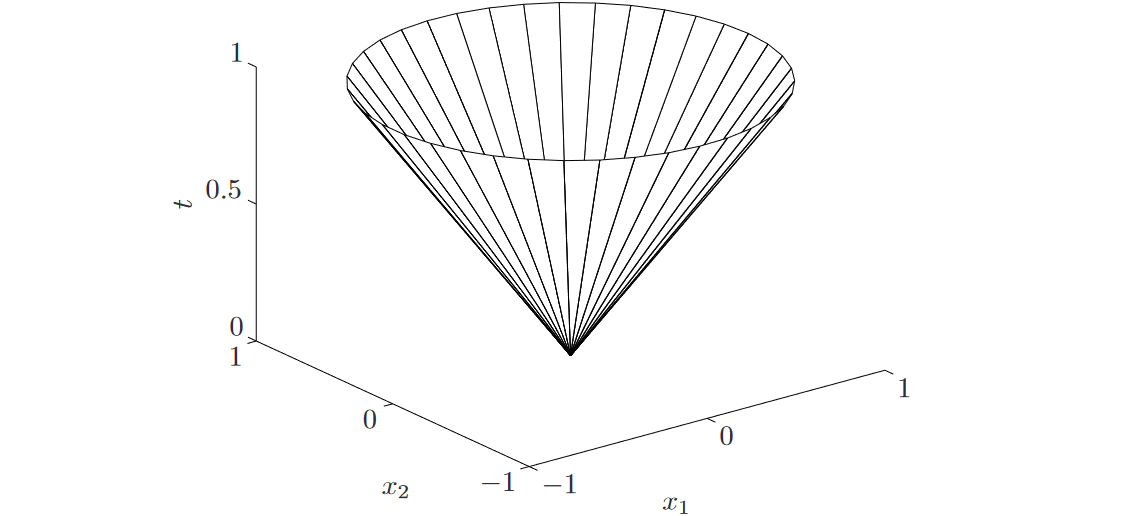
图5. \(\mathbb{R}^2\)中的二阶锥（取二范数）的边界。