【凸优化】1 仿射集，凸集，锥

1. 仿射集 Affine Sets

1）定义

定义1：\(x_1, x_2\)为集合\(C\subseteq \mathbb{R}^n\)中的任意两点，如果穿过\(x_1,x_2\)的直线仍在\(C\)内，那么\(C\)为仿射集。
定义2：对于任意\(x_1,x_2\in C\)，\(\theta\in \mathbb{R}\)，如果 \(\theta x_1+(1-\theta)x_2\in C\)，那么\(C\)为仿射集。

2）仿射组合

扩展：如果\(C\)为仿射集，\(x_1,...,x_k\in C\) 并且 \(\theta_1+...+\theta_k=1\)，那么\(\theta_1 x_1+...+\theta_k x_k\in C\)。其中，\(\theta_1 x_1+...+\theta_k x_k\)称为仿射组合（Affine Combination）。

如果\(C\)为仿射集，\(x_0\in C\)，那么\(V=C-x_0=\{x-x_0|x\in C\}\)称为与\(C\)相关的子空间。 (相当于平移)

线性方程组的解集是仿射集？证：
\(C=\{x|Ax=b\}, A\in \mathbb{R}^{m\times n}, x\in \mathbb{R}^n, b\in \mathbb{R}^m\)
对任意\(x_1,x_2\in C\) 有\(Ax_1=b, Ax_2=b\)，那么设 \(\theta \in \mathbb{R}\)，我们想证：
\(\theta x_1 +(1-\theta)x_2\)是否\(\in C\)，即
\(A(\theta x_1 +(1-\theta)x_2)\)是否\(= b\)，整理可得：
\(\theta A x_1 + (1-\theta) A x_2=\theta b+(1-\theta)b=b\)。

对集合\(V\)的分析：

\[V=\{x-x_0|x\in C\}, \forall x_0\in C \\ =\{x-x_0|Ax=b\}, Ax_0= b\\ =\{x-x_0|A(x-x_0)=0\}\\ =\{y|Ay=0\} \]

为A的零空间（null space）。

3）仿射包

仿射包(affine hull)：任意集合\(C \in \mathbb{R}^n\)，\(C\)中的点所构成的全部仿射组合的集合称为\(C\)的仿射包，记为\({\rm aff} \; C\)：

\[{\rm aff} \; C=\{\theta_1 x_1+...+\theta_k x_k|x_1,...,x_k\in C, \theta_1+...+\theta_k=1\} \]

可以看出，集合\(C\)的仿射包是包含\(C\)的最小仿射集；\(S\)是任意仿射集，如果\(C\subseteq S\)，那么\({\rm aff} \; C \subseteq S\)。

2. 凸集 Convex Sets

1）定义

定义1：\(x_1, x_2\)为集合\(C\subseteq \mathbb{R}^n\)中的任意两点，如果穿过\(x_1,x_2\)的线段仍在\(C\)内，那么\(C\)为凸集。
定义2：对于任意\(x_1,x_2\in C\)，\(\theta\in [0,1]\)，如果 \(\theta x_1+(1-\theta)x_2\in C\)，那么\(C\)为仿射集。

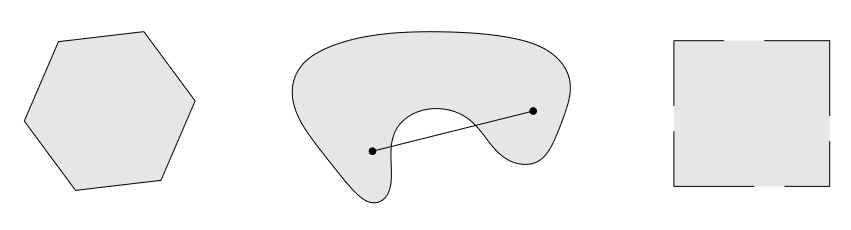
图1. 左：六边形，包括边，是凸集；中：非凸集合；右：正方形， 不包含边上的某些点，非凸（如果不含的点只在四个角上，为凸集）。

2）凸组合

类似的，\(x_1,...,x_k\)的凸组合是\(\theta_1 x_1+...+\theta_k x_k\)这样相加得到的点，其中\(\theta_1+...+\theta_k =1\)，并且\(\theta_i \in [0,1]\)，\(i=1,...,k\)。凸组合可以看做是点的混合(mixture)或加权平均(weighted average)，其中\(\theta_i\)是混合中\(x_i\)的分数。

扩展：\(C\)为凸集\(\Leftrightarrow\)(当且仅当)\(C\)中任意元素的凸组合\(\in C\)。

3）凸包

凸包(convex hull)：任意集合\(C \in \mathbb{R}^n\)，\(C\)中的点所构成的全部凸组合的集合称为\(C\)的凸包，记为\({\rm conv} \; C\)：

\[{\rm conv} \; C=\{\theta_1 x_1+...+\theta_k x_k|x_i\in C, \theta_i\in[0,1], i=1,...,k,\theta_1+...+\theta_k=1\} \]

集合\(C\)的凸包是包含\(C\)的最小凸集；\(B\)是任意凸集，如果\(C\subseteq B\)，那么\({\rm conv}\;C\subseteq B\)。

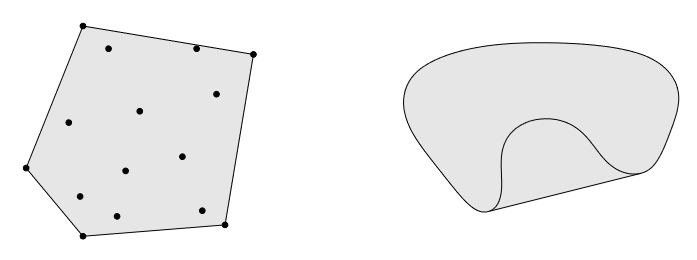
图2. \(\mathbb{R}^2\)中的两个凸包，左图中的集合（15个点构成的集合）的凸包是一个五边形（阴影部分）；右图阴影部分为图1中间的图形的凸包。

凸组合的概念也可归纳为无限累加、积分，以及最一般形式的概率分布：
设 \(\theta\) 满足：\(\sum_{i=1}^{\infty}\theta_i =1\)，\(\theta_i\in[0,1]\)，\(x_i\in C\)，其中\(C\subseteq \mathbb{R}^n\)为凸集，那么\(\sum_{i=1}^{\infty}\theta_ix_i\in C\)(如果级数收敛)。

更一般地，设 \(p:\mathbb{R}^n \rightarrow \mathbb{R}\)满足:对于所有的\(x\in C\)有\(p(x)\in [0,1]\)，并且\(\int_{C}p(x)dx=1\)，其中\(C\subseteq \mathbb{R}^n\)为凸集，那么\(\int_{C}p(x)xdx\in C\)(如果积分存在)。

3 锥 Cones

1)定义

集合\(C\)为锥（cone）\(\Leftrightarrow\)对于任意\(x\in C\)，\(\theta \geq 0\)，有\(\theta x \in C\)。
集合\(C\)为凸锥(convex cone)\(\Leftrightarrow\)对于任意\(x_1,x_2\in C\)，\(\theta_1,\theta_2 \geq 0\)，有\(\theta_1 x_1+\theta_2x_2 \in C\)。

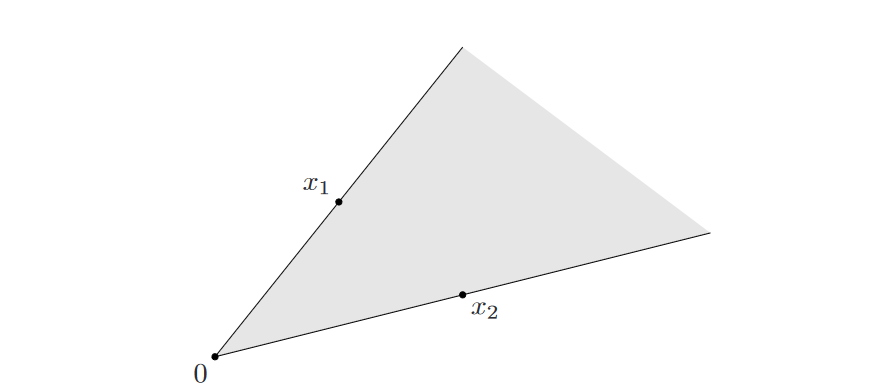
图3. 凸锥在几何上可以描述为：顶点为0且边缘穿过\(x_1\)和\(x_2\)的二维饼图

2）锥组合

\(x_1,...,x_k\)的锥组合(conic combination)为\(\theta_1 x_1 +,...,+\theta_k x_k\)这样相加得到的点，其中\(\theta_1,...,\theta_k \geq 0\)。
如果\(x_i\in C\)，\(C\) 是凸锥，那么\(x_i\)的任意锥组合在\(C\)内。
集合\(C\)是凸锥\(\Leftrightarrow\)\(C\)包含\(C\)中元素的所有的锥组合。
类似的，锥组合的概念可以一般化到无穷累加和积分。

3）锥包

集合\(C\)的锥包(conic hull)是\(C\)内点的所有锥组合构成的集合，即：

\[\{\theta_1x_1+...+\theta_kx_k|x_i\in C, \theta_i\geq 0, i=1,...,k\} \]

集合\(C\)的锥包是包含\(C\)的最小凸锥。

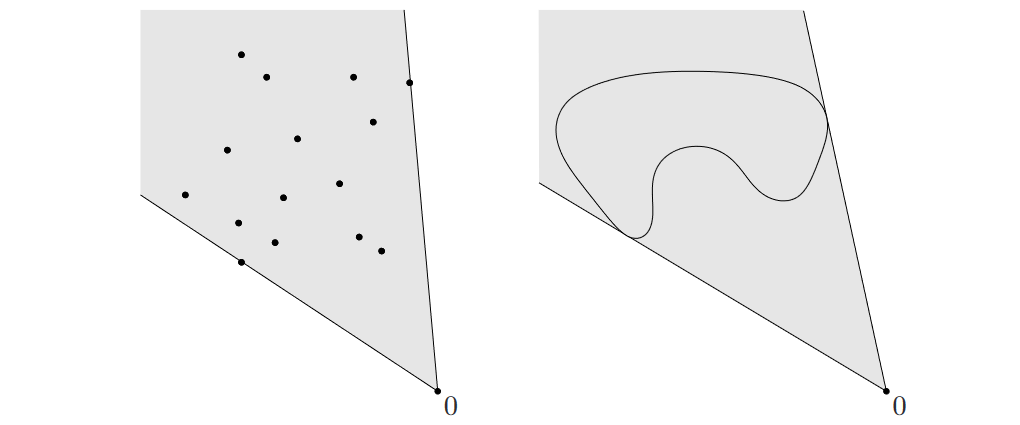
图4. 图2中的两个集合的锥包（阴影部分）；如果集合为两个点，且两点连线通过0点，它的锥包为一条通过这两点，顶点为0的射线

4 几种重要的例子

• 仿射集都是凸集。
• 任意的空集\(\varnothing\)，只包含一个点的集合\(\{x_0\}\)，和整个\(\mathbb{R}^n\)空间都是\(\mathbb{R}^n\)的仿射子集。
• 任意的直线都是仿射集，如果直线通过0点，那么它是一个凸锥。
• 任意的线段都是凸集，但不是仿射集。
• 一条射线，形式为\(\{x_0 + θv | θ \geq 0\}\)，其中 \(v \neq 0\)，是凸集，但不是仿射集。 如果\(x_0=0\)，则它是凸锥。
• 任何子空间都是仿射集，并且是凸锥。