【论文笔记】(2019,PGD)Towards Deep Learning Models Resistant to Adversarial Attacks
摘要
作者从鲁棒优化(robust optimization)的角度研究了神经网络的对抗鲁棒性(adversarial robustness)。基于鞍点公式(min-max)本文提出了一种防御任何对抗样本的方法。
1 介绍
本文的主要贡献:
- 对抗样本的生成、对抗训练(即攻击与防御)是同一的,这是一个鞍点公式(下文的公式(1))的优化问题。
- 提出了PGD(projected gradient descent)方法,是first-order中的很强的方法,作者指出,如果训练的网络对PGD攻击具有鲁棒性,那么它能够抵抗当前所有的攻击。
- 实验验证了模型容量(model capacity)大才能够抵御对抗攻击。
2 对抗鲁棒性的优化观点
考虑一个标准的分类任务,数据集为\(\mathcal{D}\),\(x\in \mathbb{R}^{d}\) 为输入样本,\(y\in [k]\) 为对应的标签。假设给定了一个合适的损失函数\(L(\theta,x,y)\)(如交叉熵),其中 \(\theta \in \mathbb{R}^{p}\) 是模型参数的集合。任务的目标是找到使 \(\mathbb{E}_{(x,y)\sim\mathcal{D}}[L(\theta,x,y)]\) 最小化的\(\theta\)。
经验风险最小化(empirical risk minimization, ERM)通常无法训练出对对抗样本具有鲁棒性的模型,为此,需要适当地增强ERM:
对于每个数据点\(x\)引入一组允许的扰动\(S\subseteq \mathbb{R}^{d}\),将其加到输入中,然后修改期望误差\(\mathbb{E}_{\mathcal{D}}[L]\)的定义:
作者将鞍点问题视为内部最大化问题(inner maximization)和外部最小化(outer minimization)问题的组合。内部最大化问题是寻找使损失最大化的对抗样本;外部最小化问题是寻找使这个损失最小化的模型参数。
2.1 攻防统一的观点
关于对抗性样本的工作主要集中在攻击和防御两方面。
攻击:著名的攻击算法FGSM使用\(x+\varepsilon {\rm sign}(\bigtriangledown_x L(\theta,x,y))\) 得到对抗样本,作者将其解释为一步的、用于最大化鞍点公式的内部的方案;据此,作者提出了PGD,是一种多步的FGSM:
(\(\Pi\)为投影符号\Pi,不是累乘)
防御:不同于把对抗样本当做数据扩充的方法,本文用对抗样本替换全部原数据样本(3.3章会进行解释)。
3 广义稳定的模型
根据公式(1)的定义,作者认为只要对抗损失足够小,就可以保证网络对任何扰动攻击都有抵抗性。所以下面只讨论公式(1)的解。
内部最大化为non-concave问题,外部最小化为non-convex问题。
3.1 对抗样本的landscape
作者选择MNIST和CIFAR10数据集,使用PGD对多个模型的局部最大值的情况进行研究:从各个评估集中的数据点的\(l_\infty\) 球内的点开始计算PGD。
实验表明:
- 对\(x+\mathcal{S}\)内的随机点执行PGD(\(l_\infty\))时,对抗损失以相当一致的方式增加并迅速稳定(如图1)。

图1. 从MNIST和CIFAR10评估数据集生成对抗性样本时的交叉熵损失值。这些图显示了在20次PGD运行期间损失的变化。每次运行都从同一自然样本的\(l_\infty\) 球中的一个均匀随机点开始。少量迭代后,对抗性损失趋于稳定。优化轨迹和最终损失值也很集中,尤其是在CIFAR10上。此外,对抗训练的网络的最终损失值明显小于标准网络。
- 进一步研究最大值的集中度:作者观察到在大量实验中,最终迭代的损失遵循一个没有极端异常值的集中分布(见图2)。
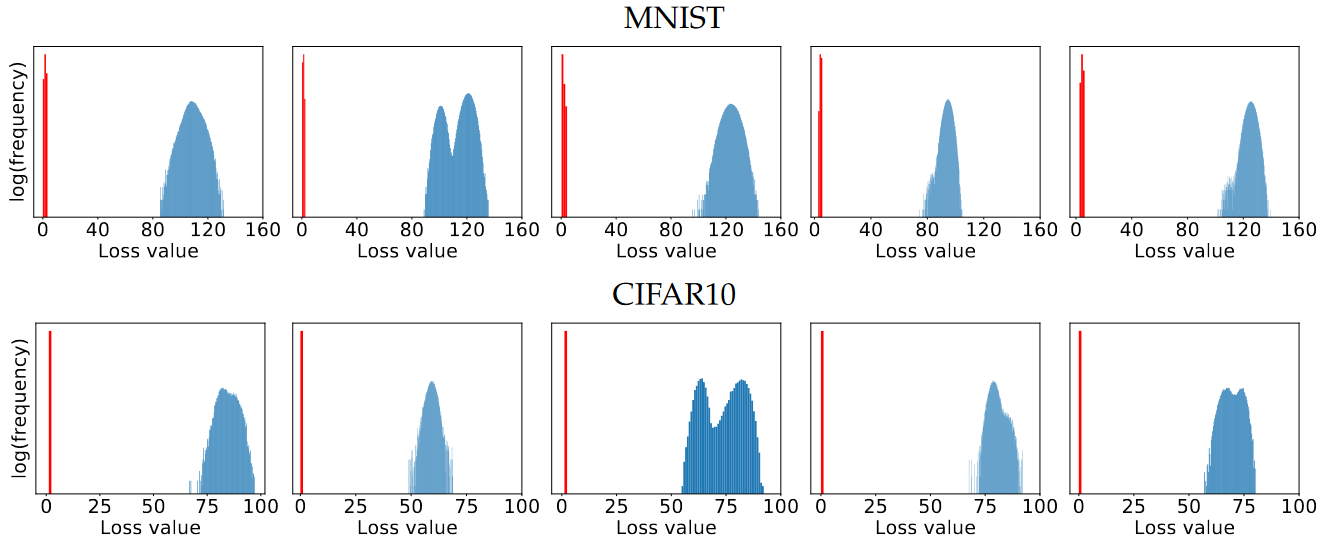
图2. 对于每个样本,从其\(l_\infty\) 球中的\(10^5\)个均匀随机点开始迭代PGD直到损失平稳。 蓝色直方图对应于标准网络上的损失,而红色直方图对应于经过对抗训练的网络损失。 对抗训练的网络的损失要小得多,最终的损失值非常集中,没有任何异常值。
3.2 一阶对抗样本
上述实验表明,无论是对于正常训练的网络还是对抗训练的网络,PGD发现的局部最大值都具有相似的损失值。作者认为只要能防御住PGD攻击,就能防住所有的一阶对抗攻击。作者还认为依赖一阶信息的攻击对于当前的深度学习是通用的。
总结就是,如果训练的网络对PGD攻击具有鲁棒性,那么它能够抵抗当前所有的攻击。
3.3 对抗训练的下降方向
接下来讨论外部最小化的优化。
在神经网络中,最小化损失函数的主要方法是随机梯度下降(Stochastic Gradient Descent,SGD)。计算外部的梯度\(\bigtriangledown_\theta\rho(\theta)\)的一种自然方法是在内部的最大值处计算损失的梯度,也就是用相应的对抗扰动替换输入点,并在扰动输入上训练网络。并且,Danskin定理表明了这是鞍点问题的有效下降方向,且内部最大值处的梯度对应于鞍点问题的下降方向。
尽管我们的问题并不满足Danskin定理的精确假设(由于ReLU和最大池,该函数不是连续可微的,而且我们只计算内部问题的近似最大化),但实验表明,仍然可以使用这些梯度来进行优化。图3可看出,作者能够可靠地对公式(1)进行优化,从而训练出鲁棒的分类器。

图3. 对抗样本训练过程中的交叉熵损失。此图说明,可以不断降低公式(1)的内部问题的值,从而产生一个越来越鲁棒的分类器。
4 模型容量和对抗鲁棒性
上述实验只是成功得到了公式(1)的解,但这不能保证得到的分类器是稳健、准确的。所以还需要证明问题的\(\textit{value}\)(即对对抗样本的最终损失)很小,非常小的\(\textit{value}\) 意味着完美的、对抗鲁棒的分类器。
对于一组固定的可能扰动\(\mathcal{S}\),\(\textit{value}\) 完全取决于分类器的架构,模型的架构容量(capacity)是影响其整体性能的主要因素。如图4,想要模型更稳定、更鲁棒,需要更复杂的决策边界,所以需要模型容量足够大。

图4. 标准的vs对抗的决策边界。左:简单的(线性的)决策边界可以轻松地将一组点分开;中:简单的决策边界没能分隔数据点周围的\(l_\infty\) 球(这里是正方形)。因此,有些对抗样本(红色星)会被错误分类。右:分隔\(l_\infty\) 球需要一个更复杂的决策边界, 由此产生的分类器对具有有界\(l_\infty\)范数扰动的对抗样本具有鲁棒性。
接下来,作者用实验验证了模型容量的重要性:
- 对于MNIST数据集,使用简单的卷积网络,不断将网络size加倍(即卷积filters的数量和全连接层的size加倍),针对不同的对抗攻击 观察网络的表现是如何变化的。
网络描述:一个带有2个过滤器的卷积层+一个带有4个过滤器的卷积层+一个带有64个单元的全连接隐藏层。卷积层之后是 2×2max-pooling 层,对抗样本由\(\varepsilon =0.3\)构建。 - 对于CIFAR10数据集,使用ResNet模型:使用随机裁剪、翻转、以及图像标准化来进行数据增强。为了增加容量,作者将包含更宽层的网络修改了10倍,使得网络有5个残差单元,每个单元有 (16, 160, 320, 640) 个过滤器。当使用自然样本进行训练时,该网络可以达到95.2%的准确率。对抗样本由\(\varepsilon =8\)构建。
实验结果如图5所示。

图5. 模型容量对模型性能的影响。前三个图/表展示了标准和对抗精度随容量的变化(a图/表 表示标准训练的两个模型在不同容量时,对自然样本、FGSM样本、PGD样本预测的准确率,b图/表 表示FGSM训练的情况下,c图/表 表示PGD训练情况下)。最后的图/表展示了对抗训练的交叉熵损失值。
作者总结了以下:
- 模型容量是有影响的
- 对于较大的$\varepsilon $,GFSM adversaries鲁棒性没增强
- 容量小的模型可能无法学习non-trivial分类器
- 随着容量的增加,\(\textit{value}\) 会降低
- 更大的容量和更强大的adversaries会降低可转移性
实验部分与相关工作两章不过多解释


 浙公网安备 33010602011771号
浙公网安备 33010602011771号