数据结构(七)高级排序算法——归并、快速排序
一、归并排序
1、排序原理
归并排序算法是一种利用了分治算法思想实现的排序算法,这种排序算法是基于有序数组合并的归并排序算法的基本思想就是:判断一个待排序序列的长度,只要这个待排序序列的长度是超过1的,那么久将这个待排序序列进行折半直到一个待排序序列的长度为1的时候,折半停止,并向上进行回溯。回溯过程相当于两个有序数组进行合并的过程。
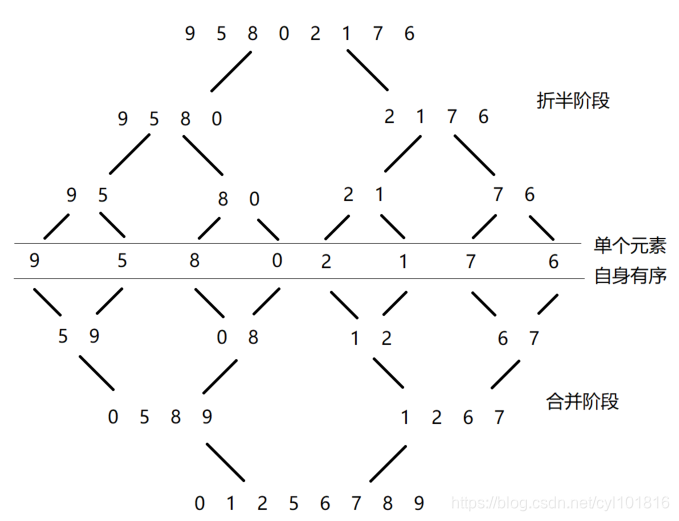
从上述流程图我们可以总结出如下归并排序的规律:
1.在折半阶段中,只要这个序列被拆分的任何一部分的长度依然是大于1的,那么就继续拆分下去
2.一个长度为n的序列,最终会被拆分为n个序列,并且这n个序列的长度都是1,在这n个序列中,单个元素自身是有序的,也就是说,当长度为n的序列被拆分成为n个子序列的时候,这n个子序列都是有序的;
3.合并阶段即排序阶段,每一次合并操作都相当于一次有序数组合并,从n个长度为1的有序序列开始,每一次合并都是如此。有序序列合并的时间复杂度是非常低的,归并排序算法也就是通过这种方式降低了自身的时间复杂度。
4.从上面的结构可以看出,在对整体序列进行拆分的时候,对于打的序列和对于相对较小的子序列的操作过程是一致的,只是序列的规模变成了原来的二分之一。那么这就说明,拆分阶段的操作,是可以使用递归的结构实现的;
5.在合并阶段,我们不得不使用一个额外的长度为n的序列来记录每一次有序序列合并的结果,并将这个结果保存回原始序列中。
2、算法实现
import java.util.Arrays;
public class MergeSort {
/**
* 归并排序的外壳,在这个方法内部会创建一个临时数组,用来为内部真正的归并排序提供辅助空间
* @param array 待排序数组
*/
public void mergeSort(int[] array) {
//创建辅助空间数组
int[] tmp = new int[array.length];
//开始真正的归并排序
mergeSortInner(array, 0, array.length-1, tmp);
}
/**
* 使用递归实现的归并排序
* @param array 待排序数组
* @param start 数组元素进行归并排序的起点下标
* @param end 数组元素进行归并排序的终点下标
* @param tmp 用来作为归并排序操作辅助空间的临时数组,临时数组长度等于原始数组长度,并且是一个空数组
*/
private void mergeSortInner(int[] array, int start, int end, int[] tmp) {
//[1]首先判断,如果数组进行归并排序的起点和中间之间所包含的元素数量不是1,那么就继续划分
if(end - start > 0) {
int middle = (start + end) / 2;
//递归调用,分别对左右两个部分进行归并排序
mergeSortInner(array, start, middle, tmp);
mergeSortInner(array, middle+1, end, tmp);
//[2]在对左右两个部分分别进行归并排序之后,左右两个部分都已经是有序的了,将左右两个部分进行有序数组合并
for(int i = start; i <= middle; i++) { //将左半部分拷贝到临时空间中
tmp[i] = array[i];
}
for(int i = middle+1; i <= end; i++) { //将右半部分拷贝到临时空间中
tmp[i] = array[i];
}
//对左右两半部分的数组进行有序数组合并操作,最终合并结果合并到原始数组中
int left = start; //控制左半部分有序数组拷贝的下标变量
int right = middle+1; //控制右半部分有序数组拷贝的下标变量
int index = start; //控制原始数组array中,有序部分合并的下标
while(left <= middle && right <= end) {
if(tmp[left] < tmp[right]) {
array[index] = tmp[left];
left++;
}else {
array[index] = tmp[right];
right++;
}
//不管是哪一边的元素落在原始数组中,原始数组的合并下标都要加一
index++;
}
//不管是左半部分没有合并完成,还是右半部分没有合并完成,都将剩余的元素全部直接落在原始数组合并完部分的后面即可
if(left <= middle) { //左边没有合并完成
while(left <= middle) {
array[index++] = tmp[left++];
}
}
if(right <= end) { //右半部分没有合并完成
while(right <= end) {
array[index++] = tmp[right++];
}
}
}else if(end - start == 0) { //[3]递归出口:如果待排序数组部分的长度是1,说明此时的待排序部分只有1个元素,那么一个元素和自己本身是有序的,此时不需要继续划分了
return;
}
}
public static void main(String[] args) {
int[] array = new int[] {7,0,1,9,2,6,3,8,5,4};
MergeSort ms = new MergeSort();
ms.mergeSort(array);
System.out.println(Arrays.toString(array));
}
}
3、时间复杂度、空进复杂度、算法稳定性分析
1、时间复杂度分析
首先在分析归并排序算法的时间复杂度之前,我们需要声明一个问题:将两个长度分别为a和b的有序序列进行合并,时间复杂度为O(a+b),然后我们根据上面的这个规律,对归并排序算法的时间复杂度进行分析:
从上面的图示可见,在合并阶段的每一层,都要将多个有序序列进行合并,但是巧合的是,这多个有序序列的总长度都是n,所在合并阶段每一层的时间复杂度都是n,那么合并阶段总共有多少层呢?我们可以尝试找到一些规律:
当待排序序列的长度是8的时候,我们恰好将有序序列分为3层;如果有序序列中只有4个元素,那么只要两层就可以了;如果有序序列中只有两个元素,一层合并就能够搞定,通过这些“巧合”的数据我们可以得出:当待排序序列的长度是n的时候,合并阶段的层数为log 2 n,即logn,综上所述:合并阶段每一层的时间复杂度是n,并且总共有logn层。所以:归并排序算法的时间复杂度是O(nlogn)。
2、空间复杂度分析
在对有序序列进行合并的时候,我们不得不使用一个长度同样为n的序列来保存每一次合并时有序数组的状态,那么我们有两种选择:
1.在每一次合并的时候都创建两个序列,分别存放两个有序子序列的内容,合并完成的结果存回原始序列中
2.总共给定一个与原始序列等长的辅助空间序列(比如一个空数组),将重复利用这个空序列,将每一次有序合并的两个序列都存放在这个空序列的制定位置上。考虑到实际开发中,在Java中new对象的操作是十分消耗时间和空间的,所以我们选择了第
二种方式进行操作。所以:归并排序算法的空间复杂度是O(n)。
3、算法稳定性分析
在归并排序算法的合并阶段,因为每一次合并都是在原始序列中相邻的一部分元素进行合并,所以不可能出现等值元素之间,相对位置发生变化的情况,所以:归并排序是一种稳定的排序算法
二、快速排序
1、排序原理
快速排序算法的思想是这样的:首先我们使用两个下标变量i和j,分别指向待排序序列的起点(i)和终点(j),然后,我们使用j变量逐步向前移动,并在移动过程中找到第一个比i下标指向元素取值更小的元素,此时j变量停下脚步,i位置上的元素和j位置上的元素进行互换。互换完毕后,换i变量向后移动,同时在移动过程中找到第一个比j变量指向元素更大的值,当找到这个值得时候,i变量停下脚步,i位置上的元素和j位置上的元素进行互换之后重复上面的两个步骤,变量i和j交互相对移动,直到ij碰面为止,然后以ij碰面的位置为中间点,将待排序序列一分为二,重复执行上面的步骤。

通过上面的图示我们可以观察得到如下几条比较重要的规律:
1.每次排序,都是下标j首先开始从后向前移动(为什么?)
2.当下标j没有遇见比下标i指向元素更小的元素的时候,j继续移动;同理,当下标i没有遇见比下标j指向元素更大的元素的时候,i继续移动
3.当ij两个下标碰面的时候,ij两个下标共同指向的元素,实际上已经“归位”了,也就是说,通过ij两个下标指向元素的不断交换,在ij碰面的时候,ij共同指向的元素此时的下标,正好是在排序完成之后这个元素应该在的位置
4.当ij碰面的时候,以ij为分界线,ij左边的元素取值都比ij位置上的元素小;ij右边的元素都比ij位置上的元素大
5.在ij碰面之后,对待排序序列进行折半,对折半后两侧的元素进行排序的操作,实际上和对整个序列进行的排序操作方式是相同的。直到折半之后,左右只剩下一个元素,或者没有剩下任何元素为止。也就是说,这个折半和排序的流程,可以使用递归实现
2、算法实现
import java.util.Arrays;
public class QuickSort {
/**
* 使用递归结构实现的快速排序
* @param array 待排序数组
* @param start 待排序部分的起点
* @param end 待排序部分的终点
*/
public void quickSort(int[] array, int start, int end) {
if(end - start > 0) { //要进行排序的部分中,包含多于一个元素的时候
//[1]先将中间元素归位
int i = start;
int j = end;
int tmp = 0; //用来进行交换的临时变量
while(i < j) {
while(i < j && array[j] >= array[i]) {
j--;
}
if(i < j) {
tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}
while(i < j && array[i] <= array[j]) {
i++;
}
if(i < j) {
tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}
}
//[2]当上述循环结束的时候,也就是ij碰面的时候,说明ij共同指向的元素已经归位了,下面只要根据归位元素,将数组分成左右两个半侧,分别执行快速排序即可
int middle = i;
// int middle = j; //此时ij相等,中间下标等于谁都是一样的
//递归调用:分别对左右两个部分的数组元素再次进行快速排序
quickSort(array, start, middle-1); //左半部分快速排序
quickSort(array, middle+1, end); //右半部分快速排序
}else if(end - start == 0) { //递归出口:如果待排序序列中的元素数量仅剩1个,那么依然是一个元素自己和自己有序,不需要继续分解
return;
}
}
public static void main(String[] args) {
int[] array = new int[] {7,0,1,9,2,6,3,8,5,4};
QuickSort qs = new QuickSort();
qs.quickSort(array, 0, array.length-1);
System.out.println(Arrays.toString(array));
}
}
3、时间复杂度、空间复杂度、算法稳定性分析
1、时间复杂度分析
通过对快速排序折半过程的分析,我们可以得到如下两点规律:
1.每一轮折半,都能够将一个元素归位
2.一个长度为n的序列能够折半多少回呢?答案是log 2 n次,即logn。所以通过上面两条规则相乘,我们能够推导出,快速排序的时间复杂度是O(nlogn)
注意:值得一说的是,如果在多线程环境下,对每一次折半之后的左右两个部分,在执行递归的时候,分别使用一个线程进行操作,能够大大提升快速排序操作的效率,但是同时涉及到了线程安全性的问题。
2、空间复杂度分析
在快速排序的折半过程中,我们只要使用一个临时变量,用于ij下标指向元素的的互换即可。所以:快速排序算法的空间复杂度是O(1)。
3、稳定性分析
快速排序算法在执行ij相向而行的过程中,很有可能将两个同值的元素的相对顺序进行改变,所以:快速排序是一种不稳定排序。





 浙公网安备 33010602011771号
浙公网安备 33010602011771号