玩具程序:bigInt
#0 为什么称作玩具程序?
1、实现简单,也就是效率一般。
2、只具备无符号数的加、乘运算功能。
#1 如何实现
以1792为例,用数组0号元素存储2,1号元素存储9,依此类推...
下面是大整数的存储结构图。
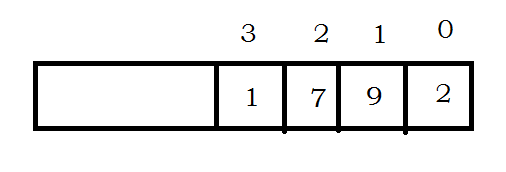
存储结构定义:
2
3 typedef struct {
4 int lastdigit;
5 char digits[MAXDIGITS];
6 } bigNum;
加法实现:按位相加,再加上进位carry。两个数长度未必相同,所以高位的处理需要特别对待。
乘法实现:乘法其实是用加法来实现的,下面列出了伪码实现。
2 bigNum result;
3 bigNum t;
4
5 for each digit x in dst{
6 some bookkeeping;
7 multiplyDigit(src, x, &t);
8 addBigNum(&result, &t);
9 }
10
11 copyBigNum(&result, src);
12
13 return 0;
14 }
#2 除了初始化bigInt外没有 除法、求余 运算:我构造了查找表,但这也使得程序代码变得更长了。
查找表的构造过程:写几行输出代码,控制台输入输出重定向,拷贝粘帖。如果是手工的话,很可能会出错。
2 0, 0, 0, 1, 0, 2, 0, 3, 0, 4,
3 0, 5, 0, 6, 0, 7, 0, 8, 0, 9,
4 1, 0, 1, 1, 1, 2, 1, 3, 1, 4,
5 1, 5, 1, 6, 1, 7, 1, 8, 1, 9,
6 2, 0, 2, 1, 2, 2, 2, 3, 2, 4,
7 2, 5, 2, 6, 2, 7, 2, 8, 2, 9,
8 3, 0, 3, 1, 3, 2, 3, 3, 3, 4,
9 3, 5, 3, 6, 3, 7, 3, 8, 3, 9,
10 4, 0, 4, 1, 4, 2, 4, 3, 4, 4,
11 4, 5, 4, 6, 4, 7, 4, 8, 4, 9,
12 5, 0, 5, 1, 5, 2, 5, 3, 5, 4,
13 5, 5, 5, 6, 5, 7, 5, 8, 5, 9,
14 6, 0, 6, 1, 6, 2, 6, 3, 6, 4,
15 6, 5, 6, 6, 6, 7, 6, 8, 6, 9,
16 7, 0, 7, 1, 7, 2, 7, 3, 7, 4,
17 7, 5, 7, 6, 7, 7, 7, 8, 7, 9,
18 8, 0, 8, 1, 8, 2, 8, 3, 8, 4,
19 8, 5, 8, 6, 8, 7, 8, 8, 8, 9,
20 9, 0, 9, 1, 9, 2, 9, 3, 9, 4,
21 9, 5
22 };
#3 阶乘运算31!,改下参数运算256!也行的, 运行时间也会长些
2 bigNum src;
3 bigNum dst;
4
5 makeBigNum(1, &src);
6
7 for (int i=1; i<32; i++){
8 makeBigNum(i, &dst);
9 multiplyBigNum(&src, &dst);
10 printfBigNum(&src);
11 }
12
13 getchar();
14 return 0;
15 }

#4 更多参考
显然,高精度数值运算程序库的编写可以称得上相当professional的工作!如果你想动手,最好找些帮手。【1】有递归实现。【2】有四则运算的完整实现。【3】有齐全的综述。【4】没看过,但显然里面会有权威的描述,必然会有的,哈哈。
【1】Eric S. Roberts. Programming Abstractions in C: A Second Course in Computer Science. Addison-Wesley Educational Publishers Inc.
【2】Steven S. Skiena Miguel A. Revilla. Programming Challenges. Springer Verlag. Ch5.2 High-Precision Integers.
【3】Steven S. Skiena. The Algorithm Design Manual, Second Edition. Springer-Verlag. Ch13.9 Arbitrary-Precision Arithmetic.
【4】D. Knuth. The Art of Computer Programming, Volume 2: Seminumerical Algorithms. Addison-Wesley, Reading MA, third edition, 1997.
#5 代码参考,拍砖请轻点下手
2 #include "bigInt.h"
3 #define MAXDIGITS 64
4
5 typedef struct {
6 int lastdigit;
7 char digits[MAXDIGITS];
8 } bigNum;
9
10 int makeBigNum(int src, bigNum * bn){
11 bn->lastdigit = -1;
12 while (src != 0){
13 bn->lastdigit ++;
14 bn->digits[bn->lastdigit] = src % 10;
15 src = src / 10;
16 }
17
18 return 0;
19 }
20
21 int printfBigNum(bigNum * bn){
22 for(int i=bn->lastdigit; i>=0; i--){
23 printf("%u", bn->digits[i]);
24 if (i%3 == 0) printf(" ");
25 }
26
27 printf("\n");
28
29 return 0;
30 }
31
32 int addBigNum(bigNum * src, bigNum * dst){
33 unsigned char cacheMgr[20][2]={
34 0, 0, 0, 1, 0, 2, 0, 3, 0, 4,
35 0, 5, 0, 6, 0, 7, 0, 8, 0, 9,
36 1, 0, 1, 1, 1, 2, 1, 3, 1, 4,
37 1, 5, 1, 6, 1, 7, 1, 8, 1, 9
38 };
39
40 bigNum * longNum = src;
41 int shortLength = dst->lastdigit;
42 if(dst->lastdigit > src->lastdigit){
43 longNum = dst;
44 shortLength = src->lastdigit;
45 }
46 int length = longNum->lastdigit;
47
48 int carry = 0;
49 for (int i=0; i<=shortLength; i++){
50 unsigned char t = src->digits[i] + dst->digits[i] + carry;
51 src->digits[i] = cacheMgr[t][1];
52 carry = cacheMgr[t][0];
53 }
54
55 for (int i=shortLength+1; i<=length; i++){
56 unsigned char t = longNum->digits[i] + carry;
57 src->digits[i] = cacheMgr[t][1];
58 carry = cacheMgr[t][0];
59 }
60
61 if (carry == 1){
62 src->lastdigit = longNum->lastdigit+1;
63 src->digits[src->lastdigit] = 1;
64 }
65 else src->lastdigit = longNum->lastdigit;
66
67 return 0;
68 }
69
70 // src =====> dst
71 int copyBigNum(bigNum * src, bigNum * dst){
72 int length = src->lastdigit;
73
74 dst->lastdigit = length;
75
76 for(int i=0; i<=length; i++)
77 dst->digits[i] = src->digits[i];
78
79 return 0;
80 }
81
82 int multiplyDigit(bigNum * src, unsigned char digit, bigNum * t){
83 unsigned char cacheMgr[96][2]={
84 0, 0, 0, 1, 0, 2, 0, 3, 0, 4,
85 0, 5, 0, 6, 0, 7, 0, 8, 0, 9,
86 1, 0, 1, 1, 1, 2, 1, 3, 1, 4,
87 1, 5, 1, 6, 1, 7, 1, 8, 1, 9,
88 2, 0, 2, 1, 2, 2, 2, 3, 2, 4,
89 2, 5, 2, 6, 2, 7, 2, 8, 2, 9,
90 3, 0, 3, 1, 3, 2, 3, 3, 3, 4,
91 3, 5, 3, 6, 3, 7, 3, 8, 3, 9,
92 4, 0, 4, 1, 4, 2, 4, 3, 4, 4,
93 4, 5, 4, 6, 4, 7, 4, 8, 4, 9,
94 5, 0, 5, 1, 5, 2, 5, 3, 5, 4,
95 5, 5, 5, 6, 5, 7, 5, 8, 5, 9,
96 6, 0, 6, 1, 6, 2, 6, 3, 6, 4,
97 6, 5, 6, 6, 6, 7, 6, 8, 6, 9,
98 7, 0, 7, 1, 7, 2, 7, 3, 7, 4,
99 7, 5, 7, 6, 7, 7, 7, 8, 7, 9,
100 8, 0, 8, 1, 8, 2, 8, 3, 8, 4,
101 8, 5, 8, 6, 8, 7, 8, 8, 8, 9,
102 9, 0, 9, 1, 9, 2, 9, 3, 9, 4,
103 9, 5
104 };
105
106 int carry = 0;
107 int length = src->lastdigit;
108 int x;
109
110 for(int i=0; i<=length; i++){
111 x = src->digits[i] * digit + carry;
112 t->lastdigit++;
113 t->digits[t->lastdigit] = cacheMgr[x][1];
114 carry = cacheMgr[x][0];
115 }
116
117 if (carry > 0){
118 t->lastdigit = t->lastdigit+1;
119 t->digits[t->lastdigit] = carry;
120 }
121
122 return 0;
123 }
124
125 int multiplyBigNum(bigNum * src, bigNum * dst){
126 bigNum result;
127 bigNum t;
128
129 makeBigNum(0, &result);
130
131 int length = dst->lastdigit;
132 for (int i=0; i<=length; i++){
133 t.lastdigit = i-1;
134 for (int s=1; s<=i; s++)
135 t.digits[s-1] = 0;
136 multiplyDigit(src, dst->digits[i], &t);
137 addBigNum(&result, &t);
138 }
139
140 copyBigNum(&result, src);
141
142 return 0;
143 }
144
145 int main(){
146 bigNum src;
147 bigNum dst;
148
149 makeBigNum(1, &src);
150
151 for (int i=1; i<32; i++){
152 makeBigNum(i, &dst);
153 multiplyBigNum(&src, &dst);
154 printfBigNum(&src);
155 }
156
157 getchar();
158 return 0;
159 }



